甲、乙两人同时从同一地点出发沿同一环形跑道进行健身锻炼，甲跑步，乙走路。若甲追上乙所需时间是两人相向而行相遇所需时间的3倍，则甲、乙的速度之比是：A.3︰1 B.5︰2 C.2︰1 D.3︰2

题目
甲、乙两人同时从同一地点出发沿同一环形跑道进行健身锻炼，甲跑步，乙走路。若甲追上乙所需时间是两人相向而行相遇所需时间的3倍，则甲、乙的速度之比是：

A.3︰1
B.5︰2
C.2︰1
D.3︰2
相似考题

1.甲、乙在一条长400米的环形跑道上锻炼，甲每分钟跑260米，乙每分钟跑210米，如果两人同时从同一地点向同一方向出发，经过多少分钟两人第三次相遇？（ ）A.16B.20C.24D.28

2.甲、乙两人练习跑步，若甲让乙先跑10米，则甲跑5秒可以追上乙；若乙比甲先跑2秒，则甲跑4秒可以追上乙。问：甲、乙的速度各是多少?（ ）A．8，5B．5，8C．6，4D．4，6

3.已知甲的步行的速度是乙的1.4倍。甲、乙两人分别由A，B两地同时出发。如果相向而行。0.5小时后相遇；如果他们同向而行，那么甲追上乙需要多少小时？（ ）A．1.5B．2C．3D．4

4.A、B两地间有条公路，甲、乙两人分别从A、B两地出发相向而行，甲先走半小时后，乙才出发，一小时后两人相遇，甲的速度是乙的睾。问甲、乙所走的路程之比是多少? A．5：6 B．1：1 C．6：5 D．4：3

更多“甲、乙两人同时从同一地点出发沿同一环形跑道进行健身锻炼，甲跑步，乙走路。若甲追上乙所需时间是两人相向而行相遇所需时间的3倍，则甲、乙的速度之比是：”相关问题

  • 第1题：

    周长为400米的圆形跑道上， 有相距100米的A、B两点， 甲乙两人分别从A、B两点同时相背而跑， 两人相遇后， 乙即转身与甲同向而跑步， 当甲跑到A时， 乙恰好跑到B。如果以后甲、乙跑的速度方向都不变，那么甲追上乙时，甲从出发开始，共跑了( )米。

    A．600

    B．800

    C．900

    D．1000


    正确答案：D
    13．D【解析】乙从相遇点C跑回B点时，甲从C过B到A，他比乙多跑了100米，乙从B到C时， 甲从A到C， 说明A到C比B到C多100米， 跑道周长400米， 所以8到C是100米，A到C是200米，甲跑200米，比乙多100米。甲追上乙要多跑300=400—100(米)，所以甲要跑200X 3=600(米)，加上开始跑的一圈，甲共跑600+400=1000(米)。

  • 第2题：

    跑马场一周之长为1080米。甲、乙两人骑自行车从同一地点同时出发，朝同一方向行驶，经过54分后，甲追上了乙。如果甲每分减少50米，乙每分增加30米，从同一地点同时背向而行，则经过3分后两人相遇。原来甲、乙两人每分各行多少米?（ ）

    A．200 180

    B．360 240

    C．240 200

    D．240 180


    正确答案：A

  • 第3题：

    甲、乙两人在圆形跑道上，同时从某地出发沿相反方向跑步。甲的速度是乙的3倍，他们第一次与第二次相遇地点之间的较短的跑道长度是100m。那么，圆形跑道的周长是（ ）m。

    A. 200
    B. 300
    C. 400
    D. 500

    答案：C
    解析：
    第一次相遇后，两人仍是沿相反方向跑步，到第二次相遇时，两人跑步距离之和为圆形跑道的周长。此时，乙跑的距离为较短的跑道，为100米，则甲跑的距离为300米，圆形跑道的周长为100 + 300 = 400(米)。故选 C。

  • 第4题：

    环形跑道的周长为400米，甲乙两人骑车同时从同一地点出发，匀速相向而行，16秒后甲乙相遇。相遇后，乙立即调头，6分40秒后甲第一次追上乙，问甲追上乙的地点距原来的起点多少米？

    A. 8
    B. 20
    C. 180
    D. 192

    答案：D
    解析：

  • 第5题：

    小李和老张同时在同一点沿同一环形跑道健身锻炼,小李跑步,老张慢走。若同向而行,小李追上老张所需时间是两人相向而行相遇所需时间的x倍。假设两人运动均为匀速,且小李跑步是老张慢走速度的y倍,则下列能反映y与x关系的是：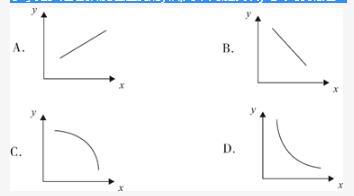

    A.如图所示
    B.如图所示
    C.如图所示
    D.如图所示

    答案：D
    解析：
    第一步，本题考查函数问题，需结合行程问题中的相遇追及问题的相关知识解题。
    第二步，设小张的速度为v，则小李的速度为yv，相遇问题公式S＝（V李＋V张）×T1＝（y＋1）vT1，追击问题公式S＝（V李－V张）×T2＝（y－1）vT2，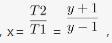

    代入特殊值确定函数图像，当y＝2时，x＝3；当y＝3时，x＝2；当y＝4时，x＝5/3；当y＝5时，x＝3/2。随着y值的增大x值逐渐减小，排除A选项，变化不成比例，不为直线，排除B选项，随着y值的增大，x值减少的趋势变小，排除C选项，只有D选项符合。
    因此，选择D选项。

  • 第6题：

    A、B两地间有条公路，甲、乙两人分别从A、B两地出发相向而行，甲先走半小时后，乙才出发，一小时后两人相遇，甲的速度是乙的2/3。甲、乙所走的路程之比是（　　）。

    A.5：6
    B.1：1
    C.6：5
    D.4：3

    答案：B
    解析：
    设甲的速度为2，则乙的速度为3。甲先走了半小时，路程是2×0．5=1。此后甲、乙各走一小时，路程分别是2、3，则甲、乙所走的路程都是3，二者之比为1：1。

  • 第7题：

    跑马场周长为1080米。甲、乙两人骑自行车从同一地点同时出发，朝同一方向行驶，经过54分钟后，甲追上了乙。如果甲每分钟减少50米，乙每分钟增加30米，从同一地点同时背向而行，则经过3 分钟后两人相遇。原来甲、乙两人每分钟各行多少米？（ ）
    A. 200 180 B. 360 240 C. 240 200 D. 240 180


    答案：A
    解析：
    ①现在甲、乙每分钟共行：1080/3=360(米)。
    ②设甲现在每分钟行x米，则原来每分钟行(x+50)米；乙现在每分钟行(360-x)米，原来每分钟行 (360-x-30)米。列方程得
    (x+ 50)X54-(360-x- 30) X 54 = 1080，解得x= 150。
    甲原来每分钟行150 + 50 = 200(米)；乙原来每分钟行360-150 - 30 = 180(米)。故本题正确答案为A。

  • 第8题：

    甲、乙两人分别从A、B两地同时出发，已知两者速度之比为7 ：5，若两人同向而行，甲追上乙需要3小时。若两人相向而行，则两人几小时后相遇？（）


    A.0.5小时
    B.1小时
    C.1.5小时
    D.2小时

    答案：A
    解析：
    令甲、乙二人速度分别为7千米/小时和5千米/小时，则AB两地相距（7-5）×3==6（千米）。若两人相向而行，则两人将在6÷（7+5）=0.5（小时）后相遇。

  • 第9题：

    单选题
    一个长方形的跑道，宽50米，长100米，甲乙两人在跑道上跑步，若两人同时同地背向出发，经30秒后相遇，若两人同时同地同向出发，经过75秒钟后，甲追上乙。现在两人在同一地点顺时针跑步，乙提前1分钟出发，问再经过多少秒甲才能追上乙？（）
    A

    35

    B

    40

    C

    45

    D

    50


    正确答案： A
    解析： 暂无解析

  • 第10题：

    甲、乙两人都以不变的速度在环形路上跑步，如果同时同地出发，相向而行，每隔2min相遇一次；如果同向而行，每隔6min相遇一次，已知甲比乙跑得快，甲乙二人每分钟各跑多少圈？

  • 第11题：

    甲、乙两人联系跑步，若让乙先跑12米，则甲经6秒追上乙，若乙比甲先跑2秒，则甲要5秒追上乙，如果乙先跑9秒，甲再追乙，那么10秒后，两人相距多少米？（ ）

    A．15

    B．20

    C．25

    D．30


    正确答案：C
    甲乙的速度差为12÷6=2米/秒，则乙的速度为2×5÷2=5米/秒，如果乙先跑9秒，甲再追乙，那么10秒后，两人相距5×9-2×10=25米。

  • 第12题：

    甲、乙两人同时从图书馆走向教室，甲一半路程步行，一半路程跑步；乙一半时间步行，一 半时间跑步，若两人步行、跑步的速度均相同，则（ ）。

    A.甲先到教室
    B.乙先到教室
    C.甲和乙同时到教室
    D.无法判断

    答案：B
    解析：
    跑步比走路快，乙用一半的时间跑步，则跑步经过的路程占总路程的一半以上。图书馆到教室的总路程是一定的，甲一半的路程跑步，而乙一半以上的路程在跑步，所以乙用的时间较短，先到教室。

  • 第13题：

    如图，在长方形跑道上，甲、乙两人分别从A、C处同时出发，按顺时针方向沿跑道匀速奔跑。已知甲、乙两人的速度分别为5米/秒、4.5米/秒。则当甲第一次追上乙时，甲沿长方形跑道跑过的圈数是：


    A.4
    B.4.5
    C.5
    D.5.5

    答案：C
    解析：
    起跑时，甲、乙相距20+12=32米，甲每秒比乙多跑5-4.5=0.5米，故甲第一次追上乙需要32/0.5=64秒。跑道一圈为（20+12）x2=64米，故甲第一次追上乙时，甲跑了64x5/64=5圈。

  • 第14题：

    甲和乙在长400米的环形跑道上匀速跑步，如两人同时从同一点出发相向而行．则第一次相遇的位置距离出发点有l50米的路程；如两人同时从同一点出发同向而行，跑得快的人第一次追上另一人时跑了（　　）米。

    A.600
    B.800
    C.1000
    D.1200

    答案：C
    解析：
    由题意可假设甲的速度为150米／秒，则乙的速度为250米／秒，甲、乙速度差为100米／秒，乙追上甲需要400÷100=4(,秒)，则所求为250×4=1000(米)。

  • 第15题：

    甲乙两人从P，Q两地同时出发相向匀速而行，5小时后于M点相遇。若其他条件不变，甲每小时多行4千米，乙速度不变，则相遇地点距M点6千米；若甲速度不变，乙每小时多行4千米，则相遇地点距M点12千米，则甲乙两人最初的速度之比为：
    A 2:1
    B 2:3
    C 5:8
    D 4:3


    答案：A
    解析：

  • 第16题：

    有一个400米环形跑道,甲、乙两人同时从同一地点同方向出发,甲以0.8米/秒的速度步行,乙以2.4米/秒的速度跑步,乙在第2次追上甲时用了（ ）秒

    A.200
    B.210
    C.230
    D.250
    E.500

    答案：E
    解析：
    乙第2次追上甲时,乙比甲多跑了2圈,即多跑了800米，故所用时间为800/（2.4-0.8）=500（秒）

  • 第17题：

    单选题
    甲、乙两人练习跑步，若让乙先跑12米，则甲经6秒追上乙；若乙比甲先跑2秒，则甲要5秒追上乙；如果乙先跑9秒，甲再追乙，那么10秒后，两人相距多少米？（　　）。
    A

    15

    B

    20

    C

    25

    D

    30


    正确答案： C
    解析：
    甲、乙的速度差为12÷6＝2米/秒，则乙的速度为2×5÷2＝5米/秒，如果乙先跑9秒，甲再追乙，那么10秒后，两人相距5×9－2×10＝25米。

相关内容