某游乐园提供打折的团体门票。当团队人数低于50时,票价为10元/人;团队人数在51-100时,票价为8元/人;团队人数超过100时,票价为5元/人。某校甲班有50多人,乙班不足50人,如果以班为单位分别购买门票,两个班一共应付944元;如果两个班联合起来作为一个团体购票,一共要付530元。问乙班有多少人: A46 B47 C48 D49
题目
A46
B47
C48
D49
相似考题
更多“某游乐园提供打折的团体门票。当团队人数低于50时,票价为10元/人;团队人数在51-100时,票价为8元/人;团队人数超过100时,票价为5元/人。某校甲班有50多人,乙班不足50人,如果以班为单位分别购买门票,两个班一共应付944元;如果两个班联合起来作为一个团体购票,一共要付530元。问乙班有多少人: ”相关问题
-
第1题:
A景区的门票价格定为100元,每天有200人前来参观旅游;但是如果将门票价格下调为80元时,则旅游者人数可达到每日260人,则当旅游者人数为260人时的门票需求价格弹性系数为()。A.2.5
B.1
C.1.5
D.0.5
参考答案:C
-
第2题:
某景点的门票价格规定如下表:
某校七年级(1)(2)班两个班共102人去游览该景点,其中(1)班人数较少,不到50人,(2)班人数较多,有50多人。如果两班都以班级为单位分别购票,则一共应付1118元;如果两班联合起来作为一个团体购票,则可以节省不少钱。问两班各有多少名学生?联合起来购票能省多少钱?

-
第3题:
有甲乙丙三个班,如果从甲班调1名学生到乙班,甲乙两班人数相等。如果从乙班抽调1名学生到丙班就比乙班多2人,甲班和丙班相比,哪个班人多?多几人?( )
A.甲班与丙班人数相等
B.甲班比丙班多2人
C.甲班比丙班多1人
D.甲班比丙班少1人
正确答案:B
根据题意设甲乙丙三个班分别为x人,y人,z人,则x一1=y+1,y一1=z+1—2,解得x=z+2。正确答案为B。 -
第4题:
某校初一年级共三个班,一班与二班人数之和为98,一班与三班人数之和为106,二班与三班人数之和为108,则二班人数为:
A.48
B.50
C.58
D.60
正确答案:B
-
第5题:
某年级有4个班,不算甲班其余三个班的总人数有131人,不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人,问这四个班共有多少人?
A.177 B.176 C.266 D.265
正确答案:A
有①乙+丙+丁=131,②甲+乙+丙=134,③乙+丙+1=甲+丁,①-③得丁-1=131-甲-丁,甲=132-2丁,①-②得,甲=丁+3,丁=43,总人数为134+43=177人 -
第6题:
某景区门票定价为每位游客100元。节假日按团队人数采取以下优惠办法:10人及以下的团队按照原价售票,超过10人的团队,其中10人按原价售票,超过10人部分的游客按照8折售票。某导游在10月1日带团到该景点旅游,买门票花掉2600元,则该旅游团共有游客A.15人
B.30人
C.25人
D.20人答案:B解析:第一步,本题为折扣类经济利润问题,采用方程法。第二步,设该团共有游客x人,由题意有10×100+(x-10)×100×0.8=2600,解得x=30。因此,选择B选项。 -
第7题:
甲、乙两个班各有40多名学生,男女生比例甲班为5:6,乙班为5:4。则这两个班的男生人数之和比女生人数之和?( )A. 多1人
B. 多2人
C. 少1人
D. 少2人答案:A解析:根据甲班男女比为5:6可知甲班人数为11的倍数,又甲、乙都是40多人,故甲班人数为44人,其中男生20,女生24人;乙班男女比为5:4可知乙班总数为9的倍数,人数为45,其中男生25人,女生20人。故两班男生人数和为20+25=45,女生人数24+20=44,男生比女生人数多1人,故本题答案为A选项。 -
第8题:
甲、乙两个班的语文平均成绩分别是80. 1和 80. 3,每班人数分别为46人和48人,经过统计检验,两班显著性差异的概率P >0. 05,这说 明( )。A.甲班好于乙班
B.甲班差于乙班
C.甲板和乙班水平无差别
D.超出统计检验范围答案:C解析:在教育统计学中常以正态曲线分布下面 积的95%或99%的理论Z值为差异显著性的临 界值。5%或1%为差异显著性水平,一般记为 a,而a决定了对原假设W。接受或拒绝的界限,其 概率为P。若样本的Z值小于1.96或2. 58,即 显著性的概率P 大于0.05或P 大于0.01,则为差异不 显著,接受假设;若样本的Z值大于1. 96或 2.58,即显著性的概率P 小于0.05或P 小于0.01,则为 差异显著,拒绝假设。 -
第9题:
旅客人数在十人(含)以上或另有规定的人数,航程、乘机日期、航班和舱位等级相同并按同一类团体票价支付票款的旅客称为()
- A、群体旅客
- B、团队旅客
- C、团体旅客
- D、同行旅客
正确答案:C -
第10题:
如乘机的团队旅客人数少于该票价规定的最低团队人数时,如客票部分未使用,应将团队旅客原付折扣票价总金额扣除该团队已使用航段的票款后,再扣除乘机旅客按正常票价计算的未使用航段票款总金额及“团体旅客自愿退票”规定的退票费,差额多退少补。
正确答案:错误 -
第11题:
某年级甲班、乙班各有男生50人。从两个班各抽取10人测量身高,并求其平均身高。如果甲班的平均身高大于乙班,能否推论甲班所有同学的平均身高大于乙班?为什么?
正确答案:不能。因为,从甲、乙两班分别抽取的10人,测量其身高,得到的分别是甲、乙两班的一个样本。样本的平均身高只是甲、乙两班所有同学平均身高的一个点估计值。即使是按随机化原则进行抽样,由于存在抽样误差,样本均数与总体均数一般很难恰好相等。因此,不能仅凭两个样本均数高低就作出两总体均数熟高熟低的判断,而应通过统计分析,进行统计推断,才能作出判断。 -
第12题:
单选题某景区门票定价为每位游客 100 元。节假日按团队人数采取以下优惠办法:10 人及以下的团队按照原价售票,超过 10 人的团队,其中 10 人按原价售票,超过 10 人部分的游客按照 8 折售票。某导游在 10 月 1 日带团到该景点旅游,买门票花掉 2600 元,则该旅游团共有游客A15 人
B30 人
C25 人
D20 人
正确答案: B解析: -
第13题:
甲乙两个班级,如果从甲班调30人到乙班,则甲班和乙班的人数比为1:1,如果从乙班调60人到甲班,则甲班和乙班的人数比为5:2,问甲乙两班共有多少人?( )
A.320
B.380
C.400
D.420
正确答案:D
设甲乙两班人数分别为x,Y。
如果从甲班调30人到乙班,则甲班和乙班的人数比为1:1,说明(X-30):(y+30)=1:1如果从乙班调60人到甲班,则甲班和乙班的人数比为5:2,说明(x+60):(y-60)=5:2解得x=240,y=180,因此甲乙两班共有420人,故应选D。 -
第14题:
四年级有4个班,不算甲班其余三个班的总人数是131人;不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少l人,问这四个班共有多少人?( )
A.177
B.178
C.264
D.26
正确答案:A
93.A [解析]由条件知:乙+丙+丁=l31,甲+乙+丙=l34,设乙、丙两班的总人数为工,则甲、丁两班的总人数为x+1,将上面两式相加得到2x+(x+1)=265,解得x=88,所以总人数为88+(88+1)=177。 -
第15题:
某年级有4个班,不算甲班其余三个班的总人数是131人;不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人,问这四个班共有多少人( )
A.177
B.176
C.266
D.265
正确答案:A设甲班a人,乙班b人,丙班C人,丁班d人,则b+C+d=131…①,a+b+C=134…②,b+C=a+d-1…③,①+②得a+2b+2C+d=265…④,③代入④得a+d=89,b+C=88,a+b+C+d=177。故选A。 -
第16题:
某校初一年级共三个班,一班与二班人数之和为98,一班与三班人数之和为106,二班与三班人数之和为108,则二班人数为多少人?( )
A.48
B.50
C.58
D.60
正确答案:B
设初一年级一、二、三班的人数分别为x、y、z,则根据题意得:
x+y=98
x+z=106
y+z=108
解得y=50,故二班人数为50人。 -
第17题:
某儿童剧以团购方式销售门票,票价如下:

现有甲、乙两所小学组织学生观看,若两所学校以各自学生人数分别购票,则两所学校门票共计需花费6120元;若两所学校将各自学生合在一起购票,则门票费为5040元。那么两所小学相差多少人?( )A.18
B.19
C.20
D.21答案:A解析:解法二:
第一步,合在一起,如果超过50人则至少需要花51×70=3570(元),而现在花了5040,说明合在一起的人数超过50人,有5040÷70=72(人)。
第二步,观察选项,两所小学相差人数在20左右,结合总人数为72可知一所小学为40多人,另一所为20多人。不合在一起平均钱数为6120÷72=85(元)。对混合平均数进行十字交叉有:

则甲、乙两小学的人数之比为3∶5,总人数为72人,故甲、乙两小学的人数差为18人。 -
第18题:
某学校有甲、乙两个班,原来甲班比乙班少20人,现在从乙班中抽调14人去甲班,则乙班是甲班的7/8,甲班原来有()人?A.50
B.53
C.55
D.60答案:A解析:
-
第19题:
某校初一年级共三个班,一班与二班人数之和为98,一班与三班人数之和为106,二班与三班人数之和为108,则二班人数为:A. 48
B. 50
C. 58
D. 60答案:B解析:此题设一班、二班、三班的人数分别为X1,X2,X3,则有: X1+X2=98 X1+X3=106 X2+X3=108,得X2=50。故答案为B。 -
第20题:
某学校有甲、乙两个班,原来甲班比乙班少20人,现在从乙班中抽调14人去甲班,则乙班是甲班的
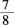
,甲班原来有( )人A.50
B.53
C.55
D.60答案:A解析:现在甲班比乙班多14x2-20=8人,则甲班现在有
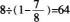
人,甲班原有64-14=50人,选择A。 -
第21题:
以下关于国内航班团队旅客说法正确的有()
- A、团队旅客"是指人数在十人(含)以上(或南航具体产品附有最低成团人数),航程、乘机日期、航班和舱位等级相同并按同一类团队票价支付票款的旅客。
- B、凡购买婴儿、儿童及其他优惠票价客票的旅客不得计算在团体人数内。
- C、团体旅客误机,客票将作废,票款不退。
- D、团队旅客中的患病旅客及其陪伴人员退票后,导致团队现有人数低于规定最低成团人数时,其余旅客需要补足团散之间的票款差额。
正确答案:A,B,C,D -
第22题:
如乘机的团队旅客人数少于该票价规定的最低团队人数时,如客票全部未使用,应按团体旅客原折扣票价总金额扣除乘机旅客按正常票价计算的票款总金额后,再扣除“团体旅客自愿退票”规定的退票费,差额多退少补。
正确答案:错误 -
第23题:
某游乐园提供打折的团体门票。当团队人数低于50时,票价为10元/人;团队人数在51-100时,票价为8元/人;团队人数超过100时,票价为5元/人。某校甲班有50多人,乙班不足50人,如果以班为单位分别购买门票,两个班一共应付944元;如果两个班联合起来作为一个团体购票,一共要付530元。问乙班有多少人?
- A、46
- B、47
- C、48
- D、49
正确答案:C -
第24题:
问答题某年级甲班、乙班各有男生50人。从两个班各抽取10人测量身高,并求其平均身高。如果甲班的平均身高大于乙班,能否推论甲班所有同学的平均身高大于乙班?为什么?正确答案: 不能。因为,从甲、乙两班分别抽取的10人,测量其身高,得到的分别是甲、乙两班的一个样本。样本的平均身高只是甲、乙两班所有同学平均身高的一个点估计值。即使是按随机化原则进行抽样,由于存在抽样误差,样本均数与总体均数一般很难恰好相等。因此,不能仅凭两个样本均数高低就作出两总体均数熟高熟低的判断,而应通过统计分析,进行统计推断,才能作出判断。解析: 暂无解析
