现有60枚1元硬币,若把它们在平面上紧密排列成正三角形,要使剩下的硬币尽可能少,则三角形的最大边长是( )。A.11 B.10 C.8 D.6
题目
B.10
C.8
D.6
相似考题
更多“现有60枚1元硬币,若把它们在平面上紧密排列成正三角形,要使剩下的硬币尽可能少,则三角形的最大边长是( )。”相关问题
-
第1题:
设有9个硬币,其中有1分、5分、3角以及5角四种,且每种硬币至少有1个。若这9个硬币总值是1.77元,则5分硬币必须有几个?()
A.1 B.2 C.3 D.4
每种硬币至少有1个,则知四种硬币各1个共0.66元,总值为1.77元,则需增加1.11元,从而需硬币1分1个,硬币5角2个,最后还需1角,从l角硬币1个或2个5分硬币中选择,题意要9个硬币,宜选择2个5分硬币,因而有3个5分硬币。故答案为C。
-
第2题:
小雨把平时节省下来的全部一角的硬币先围成一个正三角形。正好用完。后来又改围成一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用五枚硬币,那小雨所用的一角硬币合起来有多少元?( )
A.3元
B.5元
C.4元
D.6元
正确答案:D
方阵问题,运用数字特性法则即可,由硬币围成正三角形、正方形可知,硬币总价值既是3的倍数又是4的倍数,即是12角的倍数,结合选项只有6元(即60角)满足条件。 -
第3题:
设有9 个硬币,其中有 1 分、5分、1角以及 5角四种,且每种硬币至少有 1个。若这 9个硬币总值是 1.77元,则5分硬币必须有几个?( )
A.1
B.2
C.3
D.4
正确答案:C
每种硬币至少有1个,则知四种硬币各1个共0.66元,总值为1.77元,则需增加1.11元,从而需硬币1分1个,硬币5角2个,最后还需1角,从1角硬币1个或2个5分硬币中选择,题意要9个硬币,宜选择2个5分硬币,因而有3个5分硬币。故答案为C。 -
第4题:
真空中有两个点电荷+q与-q,置于边长为a的正三角形的两个顶点上,则在此正三角形的第三个顶点处的电场强度大小
为________。
正确答案:
-
第5题:
现有200根相同的钢管,把它们堆放成正三角形垛,使剩余的钢管尽可能地少,那么剩余的钢管有( )。A. 9
B. 10
C. 11
D. 12答案:B解析:S=[(1+n)n] /2≤200
n=19 时 S=190
所以还剩200-190 = 10(根),正确答案为B。 -
第6题:
有些球类比赛在开赛前用猜硬币正反面的方法来决定谁先开球。如图2所示,若裁判员以5.00m/s的速度竖直向上抛出硬币,不考虑空气阻力,则该硬币能上升的最大高度约为( )。 A.1.27m
A.1.27m
B.1.35m
C.1.40m
D.1.54m答案:A解析:硬币向上抛出后做匀减速直线运动,末速度为零,重力加速度g≈9.8m/s2。根据位移公式,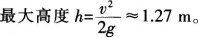
-
第7题:
有甲、乙两个人,轮流掷一枚硬币。谁先掷出反面谁赢,当然,先掷硬币的人胜率大。若甲先掷硬币,则乙的胜率为多少?A.1/3
B.1/4
C.1/6
D.1/8答案:A解析:
-
第8题:
两个质量不同的物体在同一水平面上滑行,物体与水平面间的动摩擦因数相同,比较它们滑行的最大距离,下列判断中正确的是()
- A、若两物体的初速度相等,则它们的最大滑行距离相等
- B、若两物体的初动能相等,则它们的最大滑行距离相等
- C、若两物体的初动能相等,则质量小的最大滑行距离大
- D、若两物体停止前的滑行时间相等,则两物体的最大滑行距离相等
正确答案:A,C,D -
第9题:
现有60根型号相同的圆钢管,把它堆放成正三角形垛,要使剩下的钢管尽可能少,则余下的钢管数是( )。
- A、7根
- B、6根
- C、5根
- D、4根
正确答案:C -
第10题:
小雨把平时节省下来的全部1角的硬币先围成一个正三角形,正好用完,后来又改围成一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小雨所有的1角硬币合起来总共是多少钱?()
- A、3元
- B、5元
- C、4元
- D、6元
正确答案:D -
第11题:
单选题人看到沉在水杯底的硬币,其实看到的是()。A硬币的实像,其位置比硬币实际所在位置浅
B硬币的实像,其位置即硬币的实际位置
C硬币的虚像,但位置比硬币的实际位置浅
D硬币的虚像,其位置比硬币的实际位置深
正确答案: B解析: 人看到的水杯底的硬币,实际上是由于光的折射形成的硬币的像,折射光线所成的像是由折射光线的反向延长线而不是实际光线会聚形成,所以成的像是虚像,并且折射角大于入射角,眼睛逆着光线看去,硬币的虚像位置比实际位置浅一些。 -
第12题:
单选题清点各币种现金、假币数量,清点顺序()进行加总。A成捆(把)现金 零散现金 硬币 封包现金.
B零散现金 封包现金 硬币 成捆(把)现金
C封包现金 成捆(把)现金 零散现金 硬币
D成捆(把)现金 零散现金 封包现金 硬币
正确答案: C解析: 暂无解析 -
第13题:
现有6个一元面值硬币正面朝上放在桌子上,你可以每次翻转5个硬币(必须翻转5个),问你最少经过几次翻转可以使这6个硬币全部反面朝上?
A.5次 B. 6次 C.7次 D8次
正确答案:B注意解题思路,老施历来强调归纳法,此类题应避免枚举(100枚怎么办?):
(1)每个硬币肯定都翻了奇数次;
(2)每次不动的那枚硬币肯定不同,否则原样翻回去会产生重复;(这意味机会均等,每枚硬币所翻次数必然相等)
所以,6个奇数则总次数为偶数,先排除A(25次)、C(35次)。B项6次×5=30次,平均每个5次,符合条件。D项40次不能被6整除,排除。
-
第14题:
小红把平时节省下来的全部5分硬币先围成一个正三角形,正好用完,后来又改围成一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小红所有5分硬币的总价值是( )元。
A.1
B.2
C.3
D.4
正确答案:C
设正方形每条边用2枚硬币,则正三角形每条边用(z+5)枚硬币,由题意可得等式:42-3-3(x+5)=2,解得x=16。所以小红共有60枚5分硬币,面值3元。故C是正确答案。 -
第15题:
小雨把平时节省下来的全部1角的硬币先围成一个正三角形,正好用完,后来又改围成一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小雨所有的1角硬币合起来总共是多少钱?( )
A.3元
B.5元
C.4元 >>>>>
D.6元
正确答案:D
-
第16题:
商业伦理调查人员:XYZ硬币公司通过宣传一些硬币“非常稀少”误导了消费者。实际上那些硬币相对来讲是常见的并可以很容易地买到。XYZ代理人:这是可笑的。XYZ硬币公司是世界上最大的硬币交易商之一,我们通过一家全国认可的公司来证明所有所出售的硬币的真实性,并有经营许可的硬币经销权。该XYZ代理人的回答最容易受到这样的反击:( )
A.夸大了调查人员的说法以使其显得荒谬。
B.指责调查人员有偏见,但未能提供证据来支持那种指责。
C.未能证实其他硬币交易公司没有证明所出售的硬币的真实性。
D.在不能对调查人员的指控进一步论证的情况下,列举了XYZ公司的实力。
正确答案:D
解析:的确如此,XYZ代理人在回应商业伦理调查人员的指控时,并没有拿出任何实质性的证据来反驳对方,而只是列举了自己公司的种种实力。 -
第17题:
有金、银、铜三个盒子,有一个硬币藏在其中一个盒子里,三个盒子上各贴着一张纸条,上面的提示分别是:(1)硬币在金盒子中;(2)硬币不在银盒子中; (3)硬币不在金盒子中。这三句话只有一句是真的。根据以上条件,硬币藏在哪个盒子中?
A.硬币在金盒子中 B.硬币在银盒子中 C. 硬币在铜盒子中 D. 无确切答案答案:B解析:本题属于直言判断的对当关系中的矛盾推理题。题中(1)和(3)是矛盾关系,必有一真一假,则根据“这三句话只有一句是真的”可推得(2)是假的,则知道硬帀在银盒子中。 -
第18题:
有些球类比赛会在开赛前用猜硬币正反面的方法来决定谁先开球。如图2所示,若裁判员以5.00 m/s的速度竖直向上抛出硬币,不考虑空气阻力,则该硬币能上升的最大高度约为( )。 A.1.27 m
A.1.27 m
B.1.35 m
C.1.40 m
D.1.54 m答案:A解析:硬币向上抛出的过程是匀减速直线运动,末速度为零,其中重力加速度g≈9.8 m/s2。根据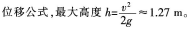
-
第19题:
TVM结账后发现有硬币未清空,下列处理正确的有?()
- A、重新结账,找零箱硬币全部清空,TVM正常投入使用
- B、重新结账仍未清空,回收硬币找零箱回AFC票务室清点确认硬币全部找回,TVM正
- C、重新结账后,循环找零箱未清空的,TVM暂停服务,AFC修复后投入使用
- D、重新结账后硬币无法清空需在《车站收入日报》备注
正确答案:A,B,C -
第20题:
内接正三角形的边长等于1.414倍的半径长度。
正确答案:错误 -
第21题:
小红把平时节省下来的全部五分硬币先围成一个三角形,正好用完,后来又改围城一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小红所有五分硬币的总价值是()
- A、1元
- B、2元
- C、3元
- D、4元
正确答案:C -
第22题:
下列系统各有多少个自由度: 1)在一平面上滑动的粒子; 2)可以在一平面上滑动并可围绕垂直于平面的轴转动的硬币; 3)一弯成三角形的金属棒在空间自由运动。
正确答案: (1)确定平面上运动的粒子需要2个独立坐标,所以自由度数为2;
(2)确定硬币的平动需要两个独立坐标,确定转动需要一个坐标,确定硬币位置共需3个坐标,所以自由度数为3;
(3)这是一个自由刚体,有6个自由度,其中3个平动自由度和3个转动自由度。 -
第23题:
单选题小红把平时节省下来的全部五分硬币先围成一个三角形,正好用完,后来又改围城一个正方形,也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币,则小红所有五分硬币的总价值是()A1元
B2元
C3元
D4元
正确答案: C解析: 正确答案是C考点和差倍比问题解析设围成三角形每条边上有x个硬币,每个顶点重复1次,则围成三角形硬币总数为3(x-1)个,同理围成正方形硬币总数为4(x-5-1),3(x-1)=4(x-5-1),解得x=21,因此共有硬币3×(21-1)=60个,总价值3元。故正确答案为C。秒杀技围成三角形正好用完说明硬币总数一定是3的倍数,因此只有C符合。
