已知有甲、乙、丙、丁四个数,甲、乙之和大于丙、丁之和,甲、丁之和大于乙、丙之和,乙、丁之和大于甲、丙之和。根根据以上请判断这四个数谁最小?() A 甲最小 B 丙最小 C 乙最小 D 丁最小
题目
已知有甲、乙、丙、丁四个数,甲、乙之和大于丙、丁之和,甲、丁之和大于乙、丙之和,乙、丁之和大于甲、丙之和。根根据以上请判断这四个数谁最小?()
A 甲最小
B 丙最小
C 乙最小
D 丁最小
A 甲最小
B 丙最小
C 乙最小
D 丁最小
相似考题
更多“已知有甲、乙、丙、丁四个数,甲、乙之和大于丙、丁之和,甲、丁之和大于乙、丙之和,乙、丁之和大于甲、丙之和。根根据以上请判断这四个数谁最小?() ”相关问题
-
第1题:
某公司有甲、乙、丙、丁四个事业部,甲和丁事业部人数之和是乙和丙人数之和的2倍,甲事业部人数是乙的5倍,丙事业部人数是丁的3倍。问丁事业部人数相当于四个事业部总人数的: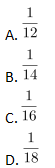 答案:B解析:解法一:
答案:B解析:解法一:
第一步,本题考查基础应用题,用方程法解题。
第二步,设丁事业部的人数为x人,则丙事业部人数为3x人。设乙事业部人数为y人,则甲事业部人数为5y人。根据“甲和丁事业部人数之和是乙和丙人数之和的2倍”可列式:5y+x=2×(y+3x),化简得3y=5x,因此四个事业部总人数为5y+y+3x+x=6y+4x=14x,则丁事业部人数相当于四个事业部总人数的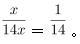
因此,选择B选项。
解法二:
第一步,本题考查基础应用题,用赋值法解题。
第二步,赋值丁事业部的人数为1人,则丙事业部的人数为3人。根据“甲和丁事业部人数之和是乙和丙人数之和的2倍”,可得到:甲+1=2×(乙+3),又因为甲是乙的5倍,因此可以求得乙为 ,甲为
,甲为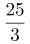 。总人数=1+3+
。总人数=1+3+ +
+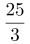 =14,因此丁占总人数的
=14,因此丁占总人数的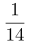 。
。
因此,选择B选项。 -
第2题:
某公司有甲、乙、丙、丁四个事业部,甲和丁事业部人数之和是乙和丙人数之和的2倍,甲事业部人数是乙的5倍,丙事业部人数是丁的3倍。问丁事业部人数相当于四个事业部总人数的:A.1/12
B.1/14
C.1/16
D.1/18答案:B解析:本题属于基础应用题。
设丁事业部的人数为x人,则丙事业部人数为3x人;乙事业部人数为y人,则甲事业部人数为5y人。根据“甲和丁事业部人数之和是乙和丙人数之和的2倍”可列式:5y+x=2×(y+3x),化简得3y=5x。四个事业部总人数为5y+y+3x+x=6y+4x=14x,则丁事业部人数相当于四个事业部总人数的 。
。
因此,选择B选项。 -
第3题:
单选题已知有甲、乙、丙、丁四个数,甲乙之和大于丙丁之和,甲丁之和大于乙丙之和,乙丁之和大于甲丙之和。根据以上请判断这四个数谁最小?( )A甲最小
B丙最小
C乙最小
D丁最小
正确答案: B解析:
由题可知:①甲+乙>丙+丁;②甲+丁>乙+丙;③乙+丁>甲+丙。由①+②可推知甲>丙,由①+③可推知乙>丙,由②+③可推知丁>丙,即丙最小。因此B项正确。 -
第4题:
甲、乙、丙、丁四人为一山区学校共捐助了 75本书,已知甲捐助的数量既是丙捐助数量的2倍与丁捐助数量之和,又是乙和丙捐助数量之和,且丙捐助数量多于丁捐助数量。则甲捐助的数量可能为()。
A.31
B.32
C.33
D.34答案:C解析:根据题意,甲=2丙+丁=乙+丙,则乙=丙+丁。设丁捐助了x,丙捐助了x+a,则乙捐助了2x+a,甲捐助了3x+2a,所以有3x+2a+2x+a+x+a+x=75,即7x+4a=75。显然7x为奇数,设x=1,则a=17,甲为37;若x=3,不存在满足条件的a;若x=5,a=10,甲为35;若x=7,不存在满足条件的a;若x=9,a=3,甲为33。结合选项知答案为C。 -
第5题:
单选题四个人的年龄之和为77岁,已知甲为10岁,他与乙的年龄之和比丙和丁的年龄之和大7岁,那么至少多少年之后丙和丁的年龄之和能够不小于77岁?( )A30
B25
C21
D17
正确答案: C解析:
10+乙=丙+丁+7,10+乙+丙+丁=77,得丙+丁=35。每过一年丙和丁的年龄和就要大两岁,(77-35)÷2=21年,因此至少需要21年之后两人的年龄和才不小于77岁。
