甲、乙、丙三个打字员，甲5天的工作量相当于乙6天的工作量；乙与丙工作能力之比为4：3，今甲、丙两人合打一份稿件，共得工资58.5元，按能力分配，甲比丙多多少元?（ ）

题目

甲、乙、丙三个打字员，甲5天的工作量相当于乙6天的工作量；乙与丙工作能力之比为4：3，今甲、丙两人合打一份稿件，共得工资58.5元，按能力分配，甲比丙多多少元?（ ）

相似考题

1.甲、乙、丙三人买书共花费96元钱，已知丙比甲多花16元，乙比甲多花8元，则甲、乙、丙三人花的钱的比是（ ）。A．3：5：4B．4：5：6C．2：3：4D．3：4：5

2.某国营农场的耕地分甲、乙、丙三个区，已知甲区的2/5等于乙区的1/2，乙、丙两区之比是4：3，且甲、乙两区的地积比乙、丙两区的地积多102公顷，问丙区有耕地多少公顷?A.250　　　　B.153　　　　C.116　　　　D.85

3.甲、乙、丙三人合修一条公路，甲、乙合修6天修好公路的1/3，乙、丙合修2天修好余下的1/4，剩余的三人又修了5天才完成。共得收入1800元，如果按工作量计酬，则乙可获得收入为（ ）A．330元B．910元C．560元D．980元

4.乙向甲借款8万元，丙又欠乙货款8万元，经过协调由丙直接向甲偿还。下列表述甲、乙、丙相互关系及性质的选项正确的是( )。A．如果甲、丙两人之间订立协议，再得到乙的同意，为债务承担B．如果乙、丙两人之间协商一致，再得到甲的同意，为债务承担C．如果甲、乙两人之间协商同意，再通知丙，为债权转移D．如果甲、乙、丙订立一个协议，对甲与乙为债权转移，对甲与丙及乙为债务承担

更多“ 甲、乙、丙三个打字员，甲5天的工作量相当于乙6天的工作量；乙与丙工作能力之比为4：3，今甲、丙两人合打一份稿件，共得工资58.5元，按能力分配，甲比丙多多少元?（ ） ”相关问题

  • 第1题：

    甲、乙、丙三个打字员，甲5天的工作量相当于乙6天的工作量；乙与丙工作能力之比为4∶3，今甲、丙两人合打一份稿件，共得工资58.5元，按能力分配，甲比丙多多少元？（）

    A. 22 B. 17.0 C. 15.5 D. 13.5


    正确答案：D

    甲5天的工作量相当于乙6天的工作量，故甲与乙的工作能力之比是6∶5，而乙与丙的工作能力之比是4∶3，由此可求出甲、乙、丙三人工作能力的比是24∶ 20∶15，从而得出甲、丙工作能力之比是24∶15，化简后得8∶5。故甲应得58.5×88+5=36元，丙应得58.5×58+5=22.5元。甲比丙多36-22.5=13.5元。

  • 第2题：

    甲、乙、丙三人共赚钱48万元。已知丙比甲少赚8万元，乙比甲少赚4万元，则甲、乙、丙赚钱的比是:

    A.2∶4∶5

    B.3∶4∶5

    C.5∶4∶2

    D.5∶4∶3


    正确答案：D

  • 第3题：

    甲、乙、丙三篮子中共有苹果57个，已知甲篮子的苹果数比乙多6个，丙篮子的苹果数比乙少3个，则甲、乙、丙三个篮子中的苹果数之比为：( )

    A.9：7：6
    B.8：6：5
    C.5：4：3
    D.5：3：2

    答案：B
    解析：
    设乙篮子的苹果数为x，则甲的为x+6，丙的为x-3。由题意知，(x+6)+x+(x-3)=57，解得x=18。则所求为(18+6)：18：(18-3)=8：6：5，B正确。

  • 第4题：

    甲、乙、丙、丁、戊五个工人，甲5天的工作量等于乙6天的工作量，乙8天的工作量等于丙10天的工作量，丙的工作效率等于丁的3/4,丁与戊的工作能力之比是8∶5,现在甲、丙两人合作15天完成的某件工程，由戊一人独做，需要多少天完成？（）

    A.50
    B.45
    C.37
    D.25

    答案：B
    解析：
    。分别用a,b,c,d,e表示甲、乙、丙、丁、戊等5人的工作效率
    则有：a:b=6:5, b:c=10:8=5:4, c:d=3:4, d:e=8:5
    逐步化为连比形式：
    a:b:c=6:5:4=18:15:12 c:d=3:4=12:16 a:b:c:d=18:15:12:16 d:e=8:5=16:10
    则a:b;c:d:e=18:15:12:16:10
    由可分别设甲、乙、丙、丁、戊的工作效率分别为18t,15t,12t,16t,10t
    甲、丙两人合作15天完成的工作量=(18t+12t)×15=450t戊一人独做，需要450t÷10t=45(天)

  • 第5题：

    甲、乙、丙共同投资， 甲的投资是乙、丙总数的1/4 ， 乙的投资是甲、丙总数的1/4 ，假如甲、乙再各投入20000元，则丙的投资还比乙多4000元，三人共投资了多少元钱。


    A. 80000
    B. 70000
    C. 60000
    D. 50000

    答案：C
    解析：
    解题指导： 假设甲乙丙投资分别是a，b，c，a=(b+c)/4;b=(a+c)/4；根据上面两个式子得到a=b ，c=b+4000+20000，a=b=12000 C=36000，12000+12000+36000=60000。因此，三人共投资是60000元。方法二：假设甲乙丙投资分别是a，b，c，a=(b+c)/4;b=(a+c)/4；根据上面两个式子得到a=b，c=b+4000+20000，a+b+c=3b+24000。答案是3的倍数。故答案为C。

  • 第6题：

    甲、乙、丙三个计算期相同的互斥方案，若有



    则各方案从优到劣的排列顺序是()。

    A、甲、乙、丙
    B、乙、丙、甲
    C、丙、乙、甲
    D、乙、甲、丙

    答案：B
    解析：

  • 第7题：

    甲、乙、丙三个地区公务员参加一次测评，其人数和如下表：

    A.乙.丙.甲
    B.乙.甲.丙
    C.甲.丙.乙
    D.丙.甲.乙
    E.丙.乙.甲

    答案：E
    解析：

  • 第8题：

    甲、乙、丙三人合修一围墙，甲、乙合修了5天完成1/3，乙、丙合修了2天完成余下的1/4，然后甲、丙两人合修了5天才完工，整个工程的劳动报酬是600元，求乙分得多少元？（ ）
    A. 105 元 B. 110 元 C. 115 元 D. 120 元


    答案：A
    解析：
    先求每天应得多少。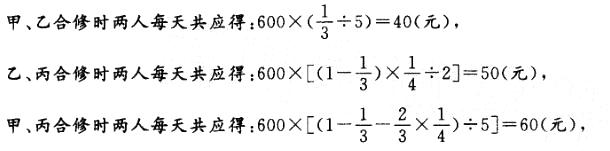

    因为丙比乙多得：60-40 = 20（元），
    故乙每天应得：(50-20)/2 = 15（元），
    所以乙一共分得：15x(5 + 2) = 105（元）。

  • 第9题：

    体育馆内正进行一场乒乓球双打比赛，观众议论双方运动员甲、乙、丙、丁的年龄： (1)“乙比甲的年龄大。” (2)“甲比他的伙伴的年龄大。” (3)“丙比他的两个对手的年龄都大。” (4)“甲与乙的年龄差距比丙与乙的年龄差距更大些。” 根据这些议论，甲、乙、丙、丁的年龄从大到小的顺序是( )。

    • A、甲、丙、乙、丁
    • B、丙、乙、甲、丁
    • C、乙、甲、丁、丙
    • D、乙、丙、甲、丁

    正确答案:D

  • 第10题：

    判断题
    甲、乙、丙三人买书共花费96元钱，已知丙比甲多花16元，乙比甲多花8元，则甲、乙、丙三人花的钱的比是3∶4∶5
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第11题：

    单选题
    甲因业务需要，以其房屋（价值11万）作抵押，分别向乙，丙二人各借款五万.甲与乙于3月10日签订抵押合同，3月20日办理了抵押登记.甲与丙于3月13日签订了抵押合同，并于同日办理了抵押登记.后甲无力还款，乙，丙将甲之房屋拍卖，只得价款8万，乙，丙如何分配 （）
    A

    乙4万，丙4万

    B

    乙5万，丙3万

    C

    丙5万，乙3万

    D

    丙4.5万，乙3.5万


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    甲、乙、丙三个计算期相同的互斥方案，若有△IRR（乙-甲）＞I，△IRR（丙-乙）＜I，△IRR（丙-甲）＞I，则各方案从优到劣的排列顺序是（）。
    A

    甲、乙、丙

    B

    乙、丙、甲

    C

    丙、乙、甲

    D

    乙、甲、丙


    正确答案： C
    解析： 暂无解析

  • 第13题：

    甲与乙签订了一份合同，约定由丙向甲履行债务，今丙履行债务的行为不符合合同的约定，甲 有权请求（ ）承担违约责任。

    A．乙

    B．乙和丙

    C．丙

    D．乙或丙


    正确答案：A
    依据我国《合同法》第六十五条规定：当事人约定由第三人向债权人履行债务的，第三人不履行债务或者履行债务不符合约定，债务人应当向债权人承担违约责任。正确答案为A。

  • 第14题：

    甲乙丙三箱水果，甲与乙的重量之比为3：4，甲与丙的重量之比为5：2，从乙箱取4千克放入丙箱，乙丙重量之比为9：4，则甲、乙、丙三箱重量之和为多少千克? A．40 B．82 C．80 D．70


    正确答案：B
    由题意可知，甲：乙：丙=15：20：6，乙、丙重量比为20：6=10：3。乙丙一共有10+3=13份．置换后重量之比为9：4，依旧是13份。因此乙减少的一份为4千克。所以乙、丙共有13x4=52千克，甲有52÷(20+6)×15=30千克。故共有52+30=82千克。

  • 第15题：

    甲、乙和丙是同一公司的同事，甲工资为8000元/月，乙工资为7200元/月，丙工资比3人工资的平均值高400元/月。问丙的工资为多少元/月

    A.7800
    B.8000
    C.8200
    D.8400

    答案：C
    解析：
    第一步，“丙工资比3人工资的平均值高400元/月”确定本题使用方程法。围绕着三人总工资等于每个人的工资的加和列方程。第二步，设3人的平均工资为x元/月，则丙的工资为（x＋400）元/月。则可列方程：3x=8000＋7200＋（x＋400）。解方程得x=7800，则丙的工资为7800＋400=8200元。因此，选择C选项。

  • 第16题：

    甲、乙、丙三人沿着环形操场跑步，乙与甲、丙的方向相反。甲每隔19分钟追上丙一次，乙每隔5分钟与丙相遇一次。如果甲与乙的速度比为5：4，那么甲的速度是丙的速度的多少倍?

    A.1．28
    B.1．6
    C. 2
    D.2.5

    答案：B
    解析：
    甲速度为5x乙速度为4x，丙速度为，'则甲追上丙一圈距离为l9(5x-y)，乙与丙相遇共同走一圈为5(4x+y)．19(5x—y)=5(4x+y)，

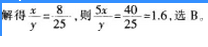
  • 第17题：

    甲、乙、丙三个计算期相同的互斥方案，若有△IRR（乙-甲）＞ic，△IRR（丙-乙）＜ic，△IRR（丙-甲）＞ic，则各方案从优到劣的排列顺序是()。

    A:甲、乙、丙
    B:乙、丙、甲
    C:丙、乙、甲
    D:乙、甲、丙

    答案：B
    解析：
    根据题目甲、乙、两三个计算期相同的互斥方案，若有△IRR（乙-甲）＞ic，则乙方案优于甲方案；根据△IRR（丙-乙）＜ic，乙方案优于丙方案；△IRR（丙-甲）＞ic，丙方案优于甲方案。所以，甲方案排在最后，其次是丙方案，乙方案最优，乙＞丙＞甲。

  • 第18题：

    甲、乙、丙、丁、戊五个工人，甲5天的工作量等于乙6天的工作量，乙8天的工作量等于丙10天的工作量，丙的工作效率等于丁的3／4，丁与戊的工作能力之比是8：5，现在甲、丙两人合作15天完成的某件工程，由戊一人独做，需要多少天完成?（　　）
    A.50天
    B.45天
    C.37天
    D.25天


    答案：B
    解析：
    根据题意设乙每天的工作量为a，则每天的工作量甲为6a／5；丙为8a／10=4a／5；丁为4a／5÷3／4=16a／15，戊为16a／15÷8／5=2a／3，甲、丙两人合作完成的某件工程为(6a／5+4a／5)×15=30a，戊一人做需要30a÷2a／3=45天。

  • 第19题：

    有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天？

    A.不到6天
    B.6天多
    C.7天多
    D.超过8天

    答案：C
    解析：
    第一步，本题考查工程问题。
    第二步，设三者工作效率分别为甲、乙、丙，根据题意则有：2乙=甲+丙，3甲+3乙+7乙+7丙=7甲+7乙+7丙→3乙=4甲，赋值甲=3，则乙=4，解得丙=5。
    第三步，B工程总量=10丙=10×5=50，即甲乙合作需要



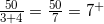
    （天），即7天多。
    因此，选择C选项。

  • 第20题：

    甲、乙、丙三人买书共花费96元钱，已知丙比甲多花16元，乙比甲多花8元，则甲、乙、丙三人花的钱的比是3∶4∶5


    正确答案:正确

  • 第21题：

    单选题
    甲、乙、丙共运来三车苹果，其中甲车比乙车多4箱，乙车比丙车多4箱，甲车比乙车每箱少3个苹果，乙车比丙车每箱少5个苹果，甲车比乙车总共多3个苹果，乙车比丙车总共多5个苹果，这三车苹果共有多少个？
    A

    628

    B

    643

    C

    658

    D

    673


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    甲、乙、丙三人合修一条公路，甲、乙合修6天修好公路的1/3，乙、丙合修2天修好余下的1/4，剩余的三人又修了5天才完成。共得收入1800元，假设他们每天的收入都为整数元，如果按工作量计酬，则乙可获得收入为？
    A

    72

    B

    96

    C

    112

    D

    132


    正确答案： A
    解析：

  • 第23题：

    单选题
    甲、乙、丙三人合修一条公路，甲、乙合修6天修好公路的1/3，乙、丙合修2天修好余下的1/4，剩余的三人又修了5天才完成。共得收入1800元，假设他们每天的收入都为整数元，如果按工作量计酬，则乙可获得收入为？
    A

    330元

    B

    910元

    C

    560元

    D

    980元


    正确答案： B
    解析：

相关内容