两个不同的圆最多可以有两个交点，那么三个不同的圆最多可以有几个交点?（ ）A．5B．6C．7D．8

题目

两个不同的圆最多可以有两个交点，那么三个不同的圆最多可以有几个交点?（ ）

A．5

B．6

C．7

D．8

相似考题

1.测设圆曲线的控制主点有()。A、起点(直圆点)、转点(曲中点)、终点(圆直点)B、交点(直圆点)、中点(曲中点)、交点(圆直点)C、交点(直圆点)、转点(曲中点)、交点(圆直点)D、起点(直圆点)、中点(曲中点)、终点(圆直点)

2.若半径不相等的两个圆有公共点，那么这两个圆的公切线最多有（ ）A．1条 B．2条 C．3条 D．4条

3.一对啮合齿廓的开始点是______；终止点是______。A.从动轮齿顶圆与啮合线的交点/主动轮齿顶圆与啮合线的交点B.主动轮齿顶圆与啮合线的交点/从动轮齿顶圆与啮合线的交点C.从动轮齿根圆与啮合线的交点/主动轮齿顶圆与啮合线的交点D.从动轮齿顶圆与啮合线的交点/主动轮齿根圆与啮合线的交点

4.两个不同的圆最多可以有两个交点，那么三个不同的圆最多可以有几个交点?A．5个 B．6个 C．7个 D．8个

参考答案和解析
正确答案：B
分析可知：三个圆两两相交，共交三次；每两个圆相交都有两个交点时，交点最多；最多的交点为3 × 2=6个。
更多“两个不同的圆最多可以有两个交点,那么三个不同的圆最多可以有几个交点?( )A.5B.6C.7 ”相关问题

  • 第1题：

    一个圆能把平面分成两个区域，两个圆可以把平面分成四个区域，问四个圆最多可能把平面分成多少个区域：

    A14
    B13
    C16
    D15


    答案：A
    解析：
    一个圆可以把平面分成两部分，两个圆交点最多有两个，没多一个交点就会多出一个部分，所以此后增加的平面部分数依次是2、4、6、8、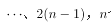个圆最多可以把平面分成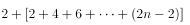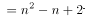个部分。因此4个园可以把平面分成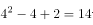部分。

    画图分析如下。

    故正确答案为A。

  • 第2题：

    若半径不相等的两个圆有公共点，那么这两个圆的公切线最多有（ ）。

    A. 1条
    B. 2条
    C. 3条
    D. 4条

    答案：C
    解析：
    半径不相等的两圆有公共点，则两圆相交、内切或外切，此时分别有2，1和3条公切线。故答案为C。

  • 第3题：

    平面上，一个圆把平面分为两个部分，两个圆最多把平面分为4个部分，3个圆最多把平面分为8个部分，那么5个圆最多把平面分为几个部分？

    A．22

    B．24

    C．26

    D．28

    E．30

    F．32

    G．20


    因为几何体为Ω的水平截面的截面积为4 π 1- y 2 +8π，该截面的截面积由两部分组成， 一部分为定值8π，看作是截一个底面积为8π，高为2的长方体得到的，对于4 π 1- y 2 ，看作是把一个半径为1， 高为2π的圆柱平放得到的，如图所示， 这两个几何体与Ω放在一起，根据祖恒原理，每个平行水平面的截面积相等，故它们的体积相等， 即Ω的体积为π?1 2 ?2π+2?8π=2π 2 +16π． 故答案为2π 2 +16π．

  • 第4题：

    两个不同的圆最多可以有两个交点，那么三个不同的圆最多可以有几个交点：
    A5个
    B6个
    C7个
    D8个


    答案：B
    解析：
    解析
    两个圆相交最多有两个交点，第三个圆与这两个圆分别相交最多增加4个交点，所以最多有6个交点。
    故正确答案为B。

  • 第5题：

    6、平面上，一个圆把平面分为两个部分，两个圆最多把平面分为4个部分，3个圆最多把平面分为8个部分，那么5个圆最多把平面分为几个部分？

    A．22

    B．24

    C．26

    D．28

    E．30

    F．32

    G．20


    C

相关内容