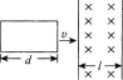
名师备选题库（九）

在恒定的匀强磁场中有一圆形闭合导体线圈,线圈平面垂直于磁场方向,要使线圈在此磁场中能产生感应电流,应使()。

A、线圈沿自身所在平面做匀速运动

B、线圈沿自身所在平面做加速运动

C、线圈绕任意一条直径做匀速转动

D、线圈绕任意一条直径做变速转动


答案：C,D

在沿水平方向的匀强磁场中，有一圆形金属线圈可绕其直径的竖直轴自由转动。开始时线圈静止，线圈平面与磁场方向既不平行也不垂直，所成的锐角为α。在磁场开始增强后

的一个极短时间内，线圈平面（ ）。

A．维持不动

B．将向使α减小的方向转动

C．将向使α增大的方向转动

D．将转动，因不知磁场方向，不能确定口会增大还是会减小


正确答案：B
由楞次定律可知，当磁场开始增强时，线圈平面转动的效果是为了减小线圈磁通量的增加，而线圈平面与磁场间的夹角越小时，通过的磁通量越小，所以将向使口减小的方向转动。

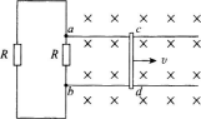
如图，间距ι=10 cm的平行光滑金属直导轨水平放置在磁感应强度B=0．5 T的匀强磁场中，磁场方向竖直向下；在平行导轨的左端a、b两点间接入两个相同电阻，阻值R=0．8Ω；电阻为r=0．1Ω的导体滑杆cd放在导轨上且与其垂直。导轨电阻不计。当cd杆以υ=2 m／s向右匀速运动时，求
（1）通过cd杆的电流；
（2）使cd杆保持匀速运动，应对它施加外力的大小和方向。


答案：
解析：
（1）cd杆匀速运动切割磁场线。设产生的电动势为E，通过cd杆的电流为I，则有

如图2-5所示，在虚线范围内有匀强磁场，磁场方向垂直纸面向里．已知矩形线圈abcd运动到图示位置时，cd边所受磁场力的方向竖直向上，则线圈的运动情形是（　　）

A.向左平动
B.向右平动
C.向上平动
D.向下平动

答案：B
解析：
本题的考点是左手定则和电磁感应． 先用左手定则确定线圈中感应电流的方向，再根据右手定则或楞次定律判断线圈的运动情况．由题意知，cd所受的磁场力方向竖直向上，磁场方向垂直纸面向里，所以根据左手定则可知cd上的感应电流的方向由d到c，线圈中感应电流的流向是dcbad（顺时针指向）．在已知感应电流方向和磁场方向的情形下，再对da用右手定则知da的运动方向是水平向右的，选B．显然，当线圈向上运动或向下运动时，线圈中磁通量不变，无感应电流，导线不受磁场力作用，C、D不正确．当线圈向左运动时，线圈进入磁场，感应电流的

如图3-11所示，一个电阻R=0．2 Ω的矩形线圈abcd．边长分别为l1=0．3 m，l2=0．2 m，沿水平方向以速度ν=5 m／s匀速地通过宽度l=0．1 m的匀强磁场（图中虚线所示范围内）．已知线圈经过磁场后释放的热量Q=0．2 J，求：
（1）磁感应强度的大小；
（2）线圈中感应电流的大小．


答案：
解析：
由图3-11见，当线圈的bc边或ad边通过磁场时，切割磁感线，线圈中有感应电流。 （1）由闭合电路的欧姆定律知感应电流为

bc和ad切割磁感线产生的感应电动势为

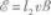
代入式①得

设bc、ad在磁场中运动的时间为t，则线圈中通过感应电流的时间为2t．由焦耳定律知线圈中产生的热量是
Q=2tI2R



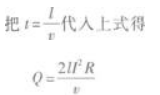
把式②代入上式得

因此，磁感应强度为

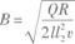
代入题给数值得

（2）线圈中的感应电流为

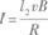
代入已知数值得

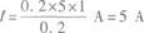
【解题指要】本题是一道电学的综合性计算题，它包含了电磁感应、闭合电路欧姆定律和
焦耳定律等知识点．
显然，当线圈右边bc进入磁场中时，切割磁感线，矩形线圈中有感应电流．同理，当线圈左边ad进入磁场中时，线圈中也有感应电流．两次电流的大小相等，通电时间相等，但在线圈中的绕行方向相反．有些考生在解本题时只考虑bc或ad中一条边进入磁场的感应电流而忽略了另一边进入磁场的感应电流．
因为线圈是电阻性的，所以电流的功全部转变为电阻上散发的热量．
在本题的条件下，解题结果与ab、cd的长度l1无关．
务必指出本题的条件是ab边的长度l1小于磁场的宽度l．如果l＞l1，线圈中感应电流的通电

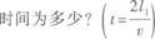
1如图所示，在空中有一水平方向的匀强磁场区域，区域的上下边缘间距为h，磁感应强度为B.有一宽度为b(bh)、长度为L、电阻为R、质量为m的矩形导线圈紧贴磁场区域的上边缘从静止起竖直下落，当线圈的PQ边到达磁场下边缘时，恰好开始做匀速运动设线圈进入磁场过程中，通过导体截面的电荷量为q1，产生的热量为Q1；线圈离开磁场过程中，通过导体截面的电荷量为q2，产生的热量为Q2则() Aq1Q2 DQ1Q2解析：选B.由于qItEt/Rn/R，进入磁场过程和离开过程的是一样的，所以q相同，所以B选项正确线圈出磁场时平均速度大于进磁场时的平均速度，出磁场时克服安培力做的功大于进磁场时克服安培力做的功，故Q1Q2，选项C、D错2.如图所示单匝三角形线圈PMN在直线边界的匀强磁场中，绕固定轴OO转动，转轴与边界重合，转轴把三角形PMN分成面积相等的两部分，t0时线圈的位置如图，规定逆时针方向为电流的正方向则下图中能正确反映线框中电流i与时间t的关系的是()解析：选A.由产生正弦交流电的条件为匀强磁场、匀速转动就可排除C、D选项再由t0时，磁通量最大，是从中性面开始转动，即I0，所以选A.3(2012泉州模拟)如图所示，倾角均为45的固定光滑金属直轨道ce和ce与半径为r的竖直光滑绝缘圆弧轨道abc和abc分别相切于c和c点，两切点与对应圆心的连线和竖直方向夹角均为45，e和e间接有阻值为R的电阻，矩形ccdd区域内存在与该平面垂直的磁场，磁感应强度BB0sineq blc(rc)(avs4alco1(f(2,x0)x)，式中x为沿直轨道向下离开边界dd的距离，且cdx0，ddL，长度也为L、阻值为R的导体棒在外力作用下，从磁场边界dd沿直轨道向下匀速通过磁场，到达边界cc时撤去外力，导体棒恰能沿圆弧轨道通过最高处aa，金属轨道电阻及空气阻力均不计，重力加速度为g，求：(1)导体棒通过aa时速度v的大小；(2)导体棒匀速通过磁场时速度v0的大小；(3)导体棒匀速通过磁场过程中棒上产生的热量Q.解析：(1)设导体棒质量为m，恰好通过圆弧轨道最高处aa满足mgmeq f(v2,r)解得veq r(gr).(2)导体棒从边界cc运动到最高处aa过程中，根据机械能守恒定律得eq f(1,2)mveq oal(2,0)eq f(1,2)mv2mg(rrcos)解得v0eq r(3r(2)gr).(3)导体棒匀速通过磁场区域历时teq f(x0,v0)棒中正弦式交流电的感应电动势eBLv0B0Lv0sineq blc(rc)(avs4alco1(f(2,x0)v0t)棒中电流的最大值Imeq f(B0Lv0,2R)eq f(B0Lr(3r(2)gr),2R)棒中电流的有效值I有eq f(Im,r(2)eq f(B0Lr(3r(2)gr),2r(2)R)导体棒产生的热量QIeq oal(2,有)Rteq f(3r(2)Boal(2,0)L2x0gr,8Rv0).答案：见解析4如图所示，MN和PQ是两根放在竖直面内且足够长的平行金属导轨，相距l50 cm，导轨处在垂直纸面向里的磁感应强度B5 T的匀强磁场中一根电阻为r0.1 的金属棒ab可紧贴导轨左右运动两块平行的、相距d10 cm、长度L20 cm的水平放置的金属板A和C分别与两平行导轨相连接，图中跨接在两导轨间的电阻R0.4 ，其余电阻忽略不计已知当金属棒ab不动时，质量m10 g、带电量q1103 C的小球以某一速度v0沿金属板A和C的中线射入板间，恰能射出金属板(g取10 m/s2)(1)求小球的速度v0；(2)若使小球在金属板间不偏转，求金属棒ab的速度大小和方向；(3)若要使小球能从金属板间射出，则金属棒ab匀速运动的速度应满足什么条件？解析：(1)根据题意，小球在金属板间做平抛运动，水平位移为金属板长L20 cm，竖直位移等于eq f(d,2)5 cm，根据平抛运动规律：eq f(d,2)eq f(1,2)gt2eq f(d,2)eq f(1,2)geq blc(rc)(avs4alco1(f(L,v0)2v0L eq r(f(g,d)2 m/s.(2)欲使小球不偏转，须小球在金属板间受力平衡，根据题意应使金属棒ab切割磁感线应产生感应电动势，从而使金属板A、C带电，在板间产生匀强电扬，小球所受电场力大小等于小球的重力由于小球带负电，电场力向上，所以电场方向向下，A板必须带正电，金属棒ab的a点应为感应电动势的正极，根据右手定则，金属棒ab应向右运动设金属棒ab的的速度为v1，则：EBlv1金属板A、C间的电压：Ueq f(Blv1,Rr)R金属板A、C间的电场E场eq f(U,d)小球受力平衡：qE场mg0联立以上各式解得：v1eq f(mgRrd,qBlR)5 m/s.(3)当金属棒ab的速度增大时，小球所受电场力大于小球的重力，小球将向上做类平抛运动，设金属棒ab的速度达到v2，小球恰沿A金属板右边缘飞出根据小球运动的对称性，小球沿A板右边缘飞出和小球沿C板右边缘飞出，其运动加速度相同，故有：qE场mgmg根据上式中结果得到：v2eq f(2mgRrd,qBlR)10 m/s所以若小球能射出金属板间，则金属棒ab的速度大小：0v10 m/s(0v10 m/s也给分)方向向右答案：见解析5如图所示，两足够长的平行光滑的金属导轨MN、PQ相距为d，导轨平面与水平面的夹角30，导轨电阻不计，磁感应强度为B的匀强磁场垂直于导轨平面向上长为d的金属棒垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量为m、电阻为R.两金属导轨的上端连接右侧电路，灯泡的电阻RL3R，电阻箱电阻调到R6R，重力加速度为g.现闭合开关S，给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为Fmg的恒力，使金属棒由静止开始运动(1)求金属棒达到最大速度一半时的加速度；(2)若金属棒上滑距离为L时速度恰达到最大，求金属棒由静止开始上滑4L的过程中，金属棒上产生的电热；(3)若改变R的阻值，当R为何值时，在金属棒达到最大速度后，R消耗的功率最大？消耗的最大功率为多少？解析：(1)金属棒先做加速度逐渐减小的加速运动，当加速度为零时，金属棒达到最大速度，此后开始做匀速直线运动设最大速度为vm，金属棒达到最大速度的一半时的加速度为a，则速度达到最大时有FIdBmgsinIBdvm/R总R总RRRL/(RRL)3R由以上各式解得vmeq f(3mgR,2B2d2)金属棒达到最大速度的一半时，、由牛顿第二定律有FI半dBmgsinamaI半Bdvm/(2R总)I/2解得ag/4.(2)设整个电路放出的电热为Q，由能量守恒定律有F4LQmgsin4Leq f(1,2)mveq oal(2,m)代入上面的vm值，可得Q2mgLeq f(9m3g2R2,8B4d4)因R/R总1/3故金属棒放出的电热QReq f(1,3)Qeq f(2,3)mgLeq f(3m3g2R2,8B4d4).(3)R上消耗的功率PI2RR并RRL/(RRL)3RR/(R3R)IRIR并Ieq f(3R,3RR) Ieq f(3Rmg,23RRBd)Peq f(m2g2,4B2d2)eq f(9R2R,3RR2)当

如图11—24所示，空间中宽度为b的区域有匀强磁场，把一个正方形导线框用外力以速度ν匀速地拉过磁场区域.已知正方形的边长为1，线圈的总电阻为R，磁感应强度是B，并有1>b，则外力做功为__________.


答案：
解析：

一矩形线圈在匀强磁场中匀速转动，当线圈通过中性面时，下列说法不正确的是（　　）

A.线圈平面与磁感线方向垂直
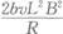
B.通过线圈的磁通量达最大值
C.通过线圈的磁通量的变化率达最大值
D.线圈中的电动势为零

答案：C
解析：

如图2-9所示，匀强磁场的磁感应强度B=0.2 T，正方形线圈每边长为0.1 m，通电流I=0.5 A，线圈所受磁场力大小是（）N，方向是（）.


答案：
解析：
1.41x10－2 水平向右 【解题指要】 本题具有一定的综合性．考查的知识点是磁场力、左手定则和力的合成．
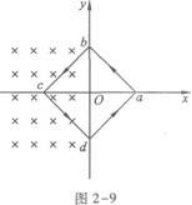
由安培力公式得Fbc=Fcd=IBL=1.0×10－2 N
用左手定则可知Fbc的方向垂直bc指向右下，Fcd的方向垂直cd指向右上，它们相互垂直，如图2-16所示．

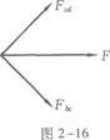
根据力的合成法则知，合力F的大小为

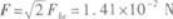
F的方向水平向右．
向考生介绍一个有用的结论：一根通电折导线在匀强磁场中所受的磁
场力等于由这根导线的起点引向终点的直导线所受的磁场力．在本题的情形下，折线bcd所受的磁场力等于直线bd所受的磁场力．由此可见

显然直接用此结论解本题要方便得多，无需分别计算Fbc和Fcd，再用力的合成计算F．

如图所示，匀强磁场区域的宽度为2，使长为d（d>l）的矩形线框以恒定速度υ向右通过磁场区域，则穿过磁场区域过程中有感应电流的时间是（??）



答案：A
解析：

在图10—19中，矩形线圈abcd的bc边悬挂在匀强磁场中．当给矩形线圈通入如图所示的电流I时，调节两盘中的砝码，使天平平衡．然后使电流I反向，这时要在天平的左盘上加质量为△m的砝码，才能使天平重新平衡．试求磁场对bc边作用力的大小．如bc边长为l，求B的大小．


答案：
解析：
当矩形线圈通以图示方向电流时，由左手定则，bc受安培力F向上，设左盘砝码的质量为

更多 “名师备选题库（九）” 相关考题
考题 填空题如图所示，abcd是一个10匝的矩形线圈，它的ab边的长度为10cm，处在一匀强磁场中，磁场方向垂直线圈平面向里，线圈通电前，天平平衡，通电后，若电流为0.1A，向右盘增加2g砝码，可使天平恢复平衡，则磁场内磁感应强度为____．（g＝10m／s）正确答案：0.2T解析：通电导体在磁场中受到安培力作用，根据左手定则可判断出运动方向和大小，F＝BIL，又根据有固定转动轴物体平衡条件得：mg＝nBIL，可得B＝0.2T．
查看答案
考题 阅读案例，并回答问题。 下面为一道物理试题和某学生的解答过程。 题目：如图6所示，水平面(纸面)内间距为2的平行金属导轨间接一电阻，质量为m、长度为l的金属杆置于导轨上。t=0时，金属杆在水平向右、大小为F的恒定拉力作用下由静止开始运动。％时刻，金属杆进入磁感应强度大小为B、方向垂直于纸面向里的匀强磁场区域，且在磁场中恰好能保持匀速运动。杆与导轨的电阻均忽略不计，两者始终保持垂直且接触良好，两者之间的动摩擦因数为μ。重力加速度大小为g。求：(1)金属杆在磁场中运动时产生的电动势的大小： (2)电阻的阻值。问题： (1)指出此道试题检测了学生所学哪些知识点 (2)给出正确解题过程。 (3)针对学生解题过程中存在问题，设计一个教学片段，帮助学生解决此类问题。答案：解析：(1)本题考查受力分析与匀速直线运动、电磁感应、欧姆定律、通电导体在磁场中受力、受力平衡等知识点。 (2)正确解题过程： 解：(1)金属杆进入磁场前做匀加速直线运动，设加速度为a，由牛顿第二定律：(3)教学片段： 师：同学们，我们先来分析一下杆的运动情况，在进入磁场前和进入磁场后，杆分别做什么运动 生：进入磁场前匀加速运动，进入磁场后匀速运动。 师：非常好。那么，匀加速的时候，对杆进行受力分析，在水平方向上杆受到了什么力 生：匀加速运动时．杆受到了拉力F和摩擦力的作用。进入磁场后，拉力和摩擦力以及安培力平衡。 师：好，我们分别来分析一下各阶段的受力。进入磁场前，拉力是固定的F，摩擦力怎么算呢 生：摩擦力等于动摩擦因数乘支持力，支持力大小等于重力大小，摩擦力大小等于μmg。金属杆与铁杆有两部分接触,所以总摩擦力应该是2μmg。 师：摩擦力大小为μ乘以导轨所受的正压力这句话表述是非常准确的，大家想一想，这里两根导轨对金属杆的正压力是多大呢是不是都等于金属杆的重力呢师：非常好，不能看到几个正压力几个接触点就简单地认为摩擦力就是几倍的μmg，考虑摩擦力一定要辨别清楚它所受到的正压力。接下来这个问题能解决了吗 生：能。
查看答案
考题 在恒定的匀强磁场中有一圆形闭合导体线圈，线圈平面垂直于磁场方向，要使线圈在此磁场中能产生感应电流，应使（）。A、线圈沿自身所在平面做匀速运动B、线圈沿自身所在平面做加速运动C、线圈绕任意一条直径做匀速转动D、线圈绕任意一条直径做变速转运正确答案:C,D
查看答案
考题 如图3所示，匝数为2：1的理想变压器、原线圈电阻为零的轨道、可在轨道上滑行的金属杆PQ形成闭合电路。闭合电路内有磁感应强度为1．0 T、方向垂直纸面向里的匀强磁场，副线圈接l0Ω的电阻，金属杆加长为PQ长为0.1m、电阻为0.4Ω。若金属杆在外力作用下以速率v=3.0m/s沿轨道匀速滑行，则下列叙述正确的是()。A.原线圈中电流大小I=0.03AB.原线圈两端电动势大小E=0.15VC.副线圈中电流大小I=0.01AD.副线圈电功率大小P=0W答案：D解析：
查看答案
考题 单选题一闭合线圈在匀强磁场中绕垂直于磁场方向的轴匀速旋转，可以产生交流电．当线圈通过中性面时（　　）．A 线圈的磁通量为零B 线圈的磁通量最大C 线圈的感应电动势最大D 线圈的磁通量变化率最大正确答案：B解析：AB两项，当线圈通过中性面时，磁场方向垂直线圈平面，此时线圈的磁通量最大；CD两项，此时线圈不切割磁感线因此没有感应电动势，线圈的磁通量变化率为零．
查看答案
考题 填空题如图所示，在磁感应强度为B的匀强磁场中，有一通电的矩形线圈，电流为I，矩形边长分别为L1和L2，磁场与线圈平面垂直，ab边受磁场力的大小为____，方向为____，线圈受磁场的合力大小为____．正确答案：BIL1,在纸面内向上,0解析：根据已知条件，ab边受到磁场力F＝BIL1，方向向上，同理cd、ad、bc也受到磁场力作用，4边两两受力大小相等、方向相反，合力大小为0．
查看答案
考题 如图所示，在匀强磁场中匀速转动的矩形线圈的周期为r，转轴0102垂直于磁场方向，线圈电阻为2Ω。从线圈平面与磁场方向平行时开始计时，线圈转过60°时的感应电流为1A。那么（　　）。 答案：A解析：从线圈平面与磁感线方向平行开始计时，正弦交变电流的感应电动势的一般表达式为e=
查看答案
考题 单选题一闭合线圈在匀强磁场中绕垂直于磁场方向的轴匀速旋转，可以产生交流电．当线圈通过中性面时（　　）．A 线圈的磁通量为零B 线圈的磁通量最大C 线圈的感应电动势最大D 线圈的磁通量变化率最大正确答案：A解析：AB两项，当线圈通过中性面时，磁场方向垂直线圈平面，此时线圈的磁通量最大；CD两项，此时线圈不切割磁感线因此没有感应电动势，线圈的磁通量变化率为零．
查看答案
考题 某N匝线圈放在匀强磁场B中，线圈的面积为S，线圈平面的法线与磁场的夹角为θ，当线圈中通入电流为I时，线圈所受的磁场力矩M为（）A、M=BIScosθB、M=NBIScosθC、M=BISsinθD、M=NBISsinθ正确答案:D
查看答案
考题 有一圆形线圈在均匀磁场中做下列几种运动，那种情况在线圈中会产生感应电流（）A、线圈平面法线沿磁场方向平移；B、线圈平面法线沿垂直于磁场方向平移；C、线圈以自身的直径为轴转动，轴与磁场方向平行；D、线圈以自身的直径为轴转动，轴与磁场方向垂直。正确答案:D
查看答案
相关内容
最新试卷
热门试卷