陕西安康旬阳桐木初级中学2016届九年级上学期期中考试数学试题
在平面直角坐标系中,点A(m,6)与点B(2.5,n)关于原点对称,则A、B两点之间的距离为( )。
A.5
B.12
C.13
D.8.5

已知A,B是抛物线y2=4x上的两个动点,且|AB|=3,则当AB的中点M到y轴的距离最短时,点M的横坐标是____.
下列平面图形中,即是轴对称图形又是中心对称图形的是( )

A.A
B.B
C.C
D.D
 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是
, 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是B.关于原点对称
C.关于直线y=x轴对称
D.以上均错

2015-2016九年级数学期中考试试题一、 选择题(共30分)1、已知点A (a, 3)与点B(1, b)关于原点对称,则a+b的值为 ()A、 -4B、-2C、2D、42、下列图形中,是中心对称图形的是() TOC o 1-5 h z 3、抛物线y=x2-mx-m2+1的图像过原点,则m的值为 ()A1B1 C -1D 04、一元二次方程x2+2x+2=0根的情况是()A 无实数根 B只有一个实数根C有两个相等的实数根D 有两个不相等的实数根5、抛物线y=-2x2不具有的性质是()A、开口向下B、对称轴是y轴 C、当x0时,y随x的增大而减小D、y有最小值6、如图,已知。0是4ABD的外接圆,AB是。0的直径,CD是炫,/ABD=58A、58?B、32?C、38?30? TOC o 1-5 h z 7、若一个三角形的两边长分别为 3和6,第三边长满足方程x2-6x+8=0,则此三 角形的周长为()A、11B、11 或 13 C、10D、138、如图,四边形ABCD内接于。0,已知/ ADC=140?,则/ AOC的度数为()A、80?B、100?C、60?D、40?9、某生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠 送一件,全组共互赠了 180件,如果全组有x名学生,则根据题意列出的方程是(A、x(x+1)=182 B、x(x-1)=182 C、x(x-1)=182X2D、x(x+1)=182X2 TOC o 1-5 h z 10、二次函数y=ax2+bx+c的图像如图所示,贝 abc, b2-4ac, 2a+b, a+b+c这四 个式子中,值为正数的有()A、 4个B、3个 C、2个D、1个二、填空题(共12分)11、如图,A、B、C是。0上的三点,/BAC=30?, WJ/BOC的大小是()。12、关于x的一元二次方程(a-2) x2+x+a2-4=0的一个根为0,则方程的另一个 根为()。13、如图,将RtABC绕直角顶点C顺时针旋转90 ,得到AA B C,连接 AA,若/ 1=26 ,则/ B的大小是()14、在函数y=x2+2x+2中,若-5&x&5,那么函数y的最大值是(三、解答题(共11题,78分) 15、(5 分)解方程:(2x-3) 2=x2 16、(5分)已知关于x的一元二次方程 mx2+x+1=0.(1)当该方程有一个根为1时,确定m的值;(2)当该方程有两个不相等的实数根时,确定 m的取值范围17、(5 分)如图,AB 是。0 的直径,/CAB= / DAB。求B证 AC=AD.18、(5分)已知关于x的二次函数的图像的顶点坐标为(-1,2),且图像过点(1,-3)。(1)求该二次函数的关系式;(2)写出它的开口方向、对称轴。19、(7分)如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点, DAE旋转后能与 DCF重合.(1)旋转中心是哪一点?(2)旋转的最小角度为多少?(3)如果连接EF,判断4DEF的形状,并说明理由20、(7)分如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度; ABC的顶点均在格点上。(1)画出 ABC关于坐标原点0成中心对称的 A1B1C1(2)以O为旋转中心将 ABC逆时针旋转90得4A2B2c2,画出AzB2c2并直 接写出C2的坐标。21 (7分)如图,AB是。0的实景,CD是。0的一条炫,且 CDLAB于点E证明:(1)/BCO=/D;若CD= 4J2 , AE=2 ,求。O的半径.22、(7分)已知抛物线y=-2x2+4x

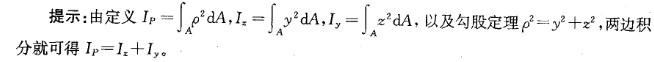
B.12
C.13
D.8.5
(2.5,-6),则 4、B 两点之间的距离就等于
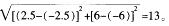
B.12
C.13
D.8.5
(2.5,-6),则 4、B 两点之间的距离就等于
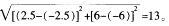
(1)直线ι经过一个定点C,试求出点C的坐标;(2分)
(2)若m=-1,已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合),且△ABP的面积为(3√13)/2,求点P的坐标。(6分)


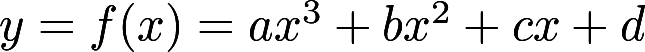 , 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是
, 若两个极值点及其对应的两个极值均为相反数, 则这个函数的图形是B.关于原点对称
C.关于直线y=x轴对称
D.以上均错

更多 “陕西安康旬阳桐木初级中学2016届九年级上学期期中考试数学试题” 相关考题
相关内容
最新试卷
热门试卷
- 2013年武汉市七一中学九年级3月月考语文试题-
- 备考2019年电大《现代汉语专题1》试题资料附答案【备考资料_
- 电大2019年《行政组织学》多套资料题汇编附答案【备考篇】_
- 电大2019年行政法与行政诉讼法选择题及考核测验题五份汇编附答案【备考资料_
- 呕心沥血整理2019年二级建造师考试建设工程施工管理个人学习笔记及试题汇编附答案精编备考可编辑_
- 2019年自考当代中国政治制度试题资料汇编附全答案【电大备考】_
- 2019年自学考试当代中国政治制度复习备考资料汇编附答案汇编【备考资料_
- 2019年自学考试当代中国政治制度自考复习资料试题汇编附答案【考前资料】_
- 2019年最新国家开 放大学电大《 城市管理学 》网络核心课形考网考作业及答案_
- 2019年最新国家开 放大学电大《管理英语3》网络核心课形考网考作业附全答案备考_
