1.矩形的判定(含答案)
在平行四边形ABCD中,∠DAB=60°,AB=15cm.已知⊙O的半径等于3cm,AB,AD分别与⊙O相切于点E,F,⊙O在平行四边形ABCD内沿AB方向滚动,与BC边相切时运动停止,试求⊙O滚过的路程.
解:

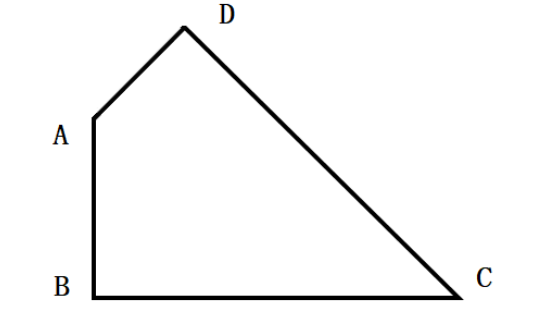
平行四边形中,已知AB、BC及其夹角∠ B(∠ B是锐角),能求出平行四边形ABCD的面积S吗?如果能,写出用AB,BC及其夹角∠ B表示S的式子。
S=BC×AB×sinB

B.矩形
C.对角线相等的四边形
D.菱形

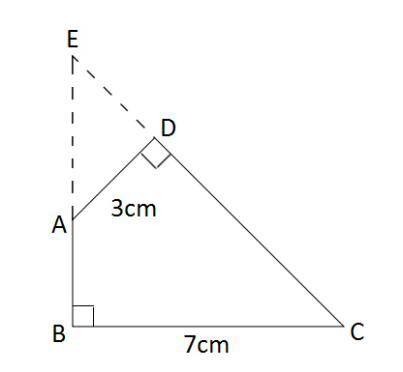
第二步,作BA和CD的延长线交于E,如图所示,得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB=135°,∠ABC=∠ADC=90°,可以求得∠DCB=360°-135°-90°×2=45°,且∠BEC=∠EAD=45°,所以△EBC和△ADE都是等腰直角三角形。
第三步,因为AD长3cm,BC长7cm,则BE=BC=7cm,DE=AD=3cm,所以
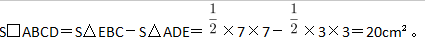
摘要:矩形的判定ABCD1.如图所示,在四边形中,已知AB∥DC,AB=DC,在不添加任何辅助线的前提下,要想该四边形为矩形,只需加上的一个条件是(填上你认为正确的一个答案即可).2.如图,已知四边形中,∠A=∠C=90∘,且ABCDAD=BC,求证:四边形ABCD是矩形.3.如图,在平行四边形∠AOB=¿ABCD中,对角线时,平行四边形AC,BDABCD交于点O,AB=OA,则当是矩形.4.下列命题中,不正确的是()A.有三个角是直角的四边形是矩形B.四个角都相等的四边形是矩形C.有一个角是直角的平行四边形是矩形D.对角线互相平分的四边形是矩形5.已知:如图,在平行四边形ABCD求证:平行四边形ABCD6.如图,在DE交△ABCBC于点中,对角线AC,BDO,∠1=∠2.相交于点是矩形.中,AB=BC,BD平分∠ABC.四边形F,连接CE.求证:四边形BECDABED是矩形.是平行四边形, 7.已知:如图,平行四边形ABCD各角的平分线分别相交于点E、F、G、H.求证:EFGH四边形是矩形.E、F8.如图,已知∘∠AEC=90为平行四边形.求证:四边形ABCDAECF的对角线上的两点,且BE=DF,为矩形.9.如图,将平行四边形ABCD的边AB延长到点E,使BE=AB,DE交边BC于点F. (1)求证:BF=CF;12(2)若∠A=∠EFC,求证:四边形BECD是矩形10.如图,四边形ABCD是平行四边形,AC,BD(1)求证:四边形ABCD是矩形;(2)若∘∠BOC=120,AB=4cm,求四边形11.如图,在△ABC平行四边形ABDE,连接中,AB=AC
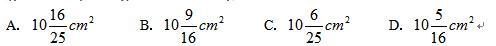


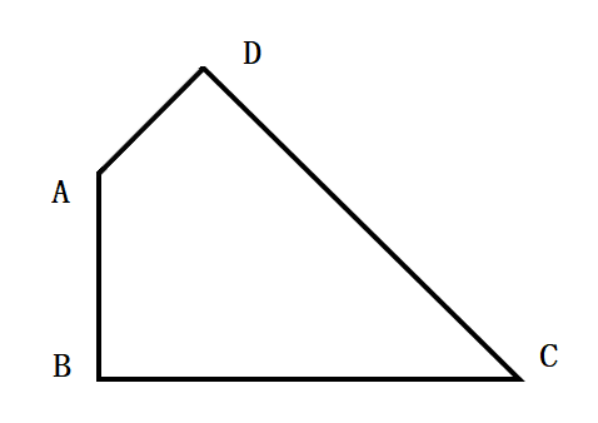
A.49/4
B.21
C.
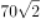
D.20