周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值越（ ）A.大 B.小 C.无法判断

题目
周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值越（ ）

A.大
B.小
C.无法判断
相似考题

1.偶函数的傅里叶级数展开式中包括()和()。

2.傅里叶级数中的系数表示谐波分量的( )。A: 相位B: 周期C: 振幅D: 频率

3.周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值()A越大B越小C不变D不一定

4.非正弦周期信号的分解可用什么方法实现：（）A.傅里叶变化；B.傅里叶变换；C.傅里叶级数展开；D.傅里叶卷积

更多“周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值越（ ）”相关问题

  • 第1题：

    一般周期信号可以利用傅里叶级数展开成()不同频率的谐波信号的线性叠加。

    A、两个

    B、多个乃至无穷多个

    C、偶数个

    D、奇数个


    参考答案：B

  • 第2题：



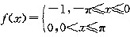
    展开成傅里叶级数时，该级数在x=0处的值为( )。



    答案：B
    解析：
    x=0是f(x)的第一类间断点，根据收敛定理，级数在点x=0处收敛于

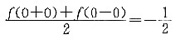
  • 第3题：

    某周期为T的非正弦周期信号分解为傅里叶级数时，其三次谐波的角频率为300πrad/s，则该信号的周期T为( )s。

    A.50
    B.0.06
    C.0.02
    D.0.05

    答案：C
    解析：
    非正弦周期信号的三次谐波的角频率为300πrad/s，则其f=50Hz。

  • 第4题：

    周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值越（ ）

    A.大
    B.小
    C.无法判断

    答案：B
    解析：

  • 第5题：

    周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值（ ）。

    A.越大
    B.越小
    C.无法确定
    D.不变

    答案：B
    解析：
    周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值越小。

  • 第6题：

    谐波含有率（HR)是指（ ）。

    A.对周期性交流量进行傅里叶分解，得到频率为基波频率的整流倍（大于1)的分量
    B从周期性交流量中减去基波分量所得的量；
    C.谐波频率与基波频率的整数比；
    D.周期性交流量中含有的第h次谐波分量的方均根值与基波分量的方均根值之比（用 百分数表示）

    答案：D
    解析：

  • 第7题：

    Acos（√31t）的傅里叶三角函数形式级数中的正弦分量幅值bn=（）


    正确答案:0

  • 第8题：

    一个非正弦周期波可分解为无限多项谐波成分，这个分解的过程称为（），其数学基础是傅里叶级数。


    正确答案:谐波分析

  • 第9题：

    周期性非正弦波的傅里叶级数展开式中，谐波的频率越高，其幅值越（）

    • A、大
    • B、小
    • C、无法判断

    正确答案:B

  • 第10题：

    某周期为0．02s的非正弦周期信号，分解成傅里叶级数时，角频率为300πrad／s的项称为（）。

    • A、三次谐波分量
    • B、六次谐波分量
    • C、基波分量
    • D、高次谐波分量

    正确答案:A

  • 第11题：

    微机保护中，电流信号工频稳定，采样值正常，不管谐波成份多么复杂，傅里叶算法都可准确计算出电流信号的工频幅值。


    正确答案:正确

  • 第12题：

    单选题
    总谐波畸变率（THD）是指（）。
    A

    周期性交流量中的谐波含量的方均根值与其基波分量的方均根值之比（用百分数表示）；

    B

    从周期性交流量t减去基波分量所得的量；

    C

    对周期性交流量进行傅里叶分解，得到频率为基波频率的整数倍（大于1）的分量；

    D

    周期性交流量的方均根值。


    正确答案： A
    解析： 暂无解析

  • 第13题：

    周期信号f(t)=－f(t±T／2),(T—周期),下列哪些不是其傅里叶级数展开式的结构特点()。

    A、只有正弦项

    B、只有余弦项

    C、只含偶次谐波

    D、只含奇次谐波


    参考答案：BCD

  • 第14题：

    某周期为0.02s的非正弦周期信号，分解成傅里叶级数时，角频率为300πrad/s的项被称为( )。

    A.三次谐波分量
    B.六次谐波分量
    C.基波分量
    D.五次谐波分量

    答案：A
    解析：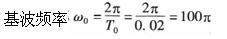

  • 第15题：

    任意给出几种常见的非正弦周期信号波形图，能否确定其傅里叶级数展开式中有无恒定量？（ ）

    A.不能
    B.能
    C.不确定
    D.分情况讨论

    答案：B
    解析：

  • 第16题：

    关于谐波分析，下列说法正确的是（ ）

    A.一个非正弦周期波可分解为无限多项谐波成分，这个分解的过程称为谐波分析
    B.谐波分析的数学基础是傅里叶级数
    C.所谓谐波分析，就是对一个已知波形的非正弦周期信号，找出它所包含的各次谐波分量的振幅和频率，写出其傅里叶级数表达式的过程
    D.方波的谐波成分中只含有正弦成分的各偶次谐波

    答案：A,B,C
    解析：
    谐波分析的数学基础是傅里叶级数，将非正弦周期信号分解为无限多项谐波成分、基波分量和直流分量。方波的谐波成分中有奇、偶次谐波。谐波分析即求解各次谐波分量的振幅和频率。

  • 第17题：

    的傅里叶展开式中，系数a3的值是（）。


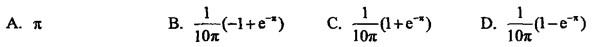    答案：C
    解析：
    提示：利用傅里叶系数公式。

  • 第18题：

    （）是指对周期性非正弦交流量进行傅里叶级数分解所得到的大于基波频率整数倍的各次分量。

    A谐波

    B基波

    C偶次谐波

    D奇次谐波


    A
    略

  • 第19题：

    任意给出几种常见的非正弦周期信号波形图，你能否确定其傅里叶级数展开式中有无恒定分量（）

    • A、不能
    • B、能
    • C、不确定

    正确答案:B

  • 第20题：

    所谓谐波分析，就是对一个已知（）的非正弦周期信号，找出它所包含的各次谐波分量的（）和（），写出其傅里叶级数表达式的过程。


    正确答案:波形；振幅；频率

  • 第21题：

    周期信号的频谱图有何特点？其傅里叶级数三角函数展开式与复指数函数展开式的频谱有何特点？


    正确答案: （1）1.离散性2.谐波性3.收敛性。（2）周期信号的傅里叶级数三角函数展开式频率谱是位于频率右侧的离散谱，谱线间隔为整数个ω。复指函数是展开式的频谱其实频谱总是偶对称的其虚频谱总是奇对称的。

  • 第22题：

    对于一个非正弦的周期量，可利用傅里叶级数展开为各种不同频率的正弦分量与直流分量，其中角频率等于ωt的称为基波分量， 角频率等于或大于2ωt的称为高次谐波。


    正确答案:正确

  • 第23题：

    填空题
    Acos（√31t）的傅里叶三角函数形式级数中的正弦分量幅值bn=（）

    正确答案： 0
    解析： 暂无解析

  • 第24题：

    单选题
    某周期为0．02s的非正弦周期信号，分解成傅里叶级数时，角频率为300πrad／s的项称为（）。
    A

    三次谐波分量

    B

    六次谐波分量

    C

    基波分量

    D

    高次谐波分量


    正确答案： A
    解析： 暂无解析

相关内容