A.为奇函数且在(－∞，0)上是减函数 B.为奇函数且在(－∞，0)上是增函数 C.为偶函数且在(0，＋∞)上是减函数 D.为偶函数且在(0，＋∞)上是增函数

题目

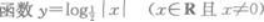
A.为奇函数且在(－∞，0)上是减函数
B.为奇函数且在(－∞，0)上是增函数
C.为偶函数且在(0，＋∞)上是减函数
D.为偶函数且在(0，＋∞)上是增函数
相似考题

1.若f(x)为(－∞,＋∞)上的任意函数,则F(x)=f(x)－f(－x)是()A、偶函数B、奇函数C、非奇非偶函数D、F(x)≡0

2.设定义域在R上的函数f(x)=x|x|，则f(x)是A．奇函数，增函数B．偶函数，增函数C．奇函数，减函数D．偶函数，减函数

3.当X>0时,f(x)=5x²＋2是()A、增函数B、减函数C、周期函数D、奇函数

4.设f(x)为连续函数，F(x)是f(x)的原函数，则（ ）。(A) 当f(x)是奇函数时，F(x)必为偶函数(B) 当f(x)是偶函数时，F(x)必为奇函数(C) 当f(x)是周期函数时，F(x)必为周期函数(D) 当f(x)是单增函数时，F(x)必为单增函数(E) 当f(x)是单减函数时，F(x)必为单减函数

参考答案和解析
答案：C
解析：
更多“A.为奇函数且在(－∞，0)上是减函数 B.为奇函数且在(－∞，0)上是增函数 C.为偶函数且在(0，＋∞)上是减函数 D.为偶函数且在(0，＋∞)上是增函数”相关问题

  • 第1题：

    下列函数中，既是偶函数，又在区间（0，3）上为减函数的是 （ ）

    A.A

    B.B

    C.C

    D.D


    正确答案：A
    本题主要考查的知识点为偶函数和减函数的性质．【应试指导】易知，A、C项为偶函数，B、D项为非奇非偶函数．在区间(0，3)上，C项中的函数为增函数，而A项中y=COSx的减区间为(2kπ，2kπ+π)，故y=COSx在(0，3)上为减函数．

  • 第2题：

    设函数f(x)在(-∞，+∞)上是偶函数，且在(0，+∞)内有f'(x)＞0， f''(x)＞0，则在(-∞，0)内必有：
    A. f'(x)＞0， f''(x)＞0 B.f'(x)＜0， f''(x)＞0
    C. f'(x)＞0， f''(x)＜0 D. f'(x)＜0， f''(x)＜0


    答案：B
    解析：
    提示：已知f(x)在(-∞，+∞)上是偶函数，函数图像关于y轴对称，已知函数在(0，+∞)，f'(x)＞0， f''(x)＞0，表明在(0，+∞)上函数图像为单增且凹向，由对称性可知，f(x)在(-∞，0)单减且凹向，所以f'(x)＜0， f''(x)＞0。

  • 第3题：

    f(χ)为偶函数，在(0，+∞)上为减函数，若，则方程f(χ)=0的根的个数是（ ）

    A.2
    B.2或1
    C.3
    D.2或3

    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为偶函数的性质． 【应试指导】由已知f(χ)为偶函数，f(χ)关于Y轴对称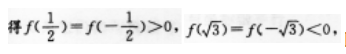，由函数连续性知，函数值由负变为正，χ由1/2变化到√3，函数值由正变为负，故方程f(χ)=0的根的个数是2(用图表示，如下图)．

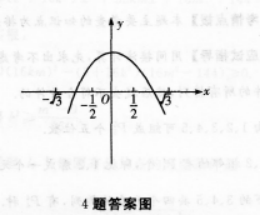
  • 第4题：


    A.连续的奇函数
    B.连续的偶函数
    C.在x=0间断的奇函数
    D.在x=0间断的偶函数

    答案：B
    解析：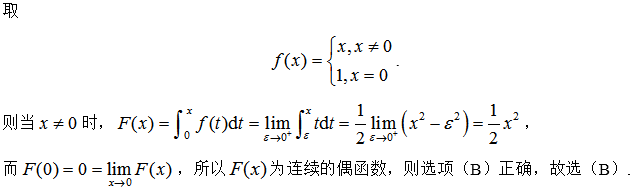

  • 第5题：

    设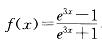，则：

    A.f(x)为偶函数，值域为(-1，1)
    B.f(x)为奇函数，值域为(-∞，0)
    C.f(x)为奇函数，值域为(-1，1)
    D.f(x)为奇函数，值域为(0，+∞)

    答案：C
    解析：

  • 第6题：



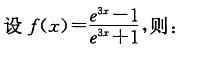    A.f（X）为偶函数，值域为（-1，1）
    B.f（X）为奇函数，值域为（-∞，0）
    C.f（X）为奇函数，值域为（-1，1）
    D.f（X）为奇函数，值域为（0，+∞）

    答案：C
    解析：

  • 第7题：


    A.该信号是奇函数且在一个周期的平均值为零，所以傅立叶系数a0和bn是零
    B.该信号是偶函数且在一个周期的平均值不为零，所以傅立叶系数a0和an不是零
    C.该信号是奇函数且在一个周期的平均值不为零，所以傅立叶系数a0和bn不是零
    D.该信号是偶函数且在一个周期的平均值为零，所以傅立叶系数a0和bn是零

    答案：B
    解析：
    从信号的波形图可以看出信号关于y轴对称，所以是偶函数，信号取值均大于0，所以在一个周期的平均值不为零。傅立叶系数a0和an分别表示信号的平均分量和谐波分量，三角波是高次谐波信号，所以傅立叶系数a0和an不是零。

  • 第8题：


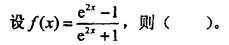
    A. f(x)为偶函数，值域为(-1,1) B. f(x)为奇函数，值域为(-∞，0)
    C.f(x)为奇函数，值域为(-1,1) D. f(x)为奇函数，值域为(0,+∞)


    答案：C
    解析：
    正确答案是C。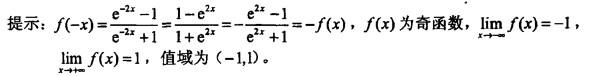

  • 第9题：

    已知定义在实数集R上的偶函数?(x)在区间[0，+∞)上为单调增函数，若?(1)

    答案：
    解析：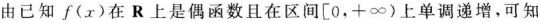

  • 第10题：

    设f（x）在（-a，a）（a＞0）上连续，F（x）是f（x）的一个原函数，则当f（x）是偶函数时，下面结论正确的是（）。

    • A、F（x）是偶函数
    • B、F（x）是奇函数
    • C、F（x）可能是奇函数，也可能是偶函数
    • D、F（x）是否是偶函数不能确定

    正确答案:D

  • 第11题：

    单选题
    如果奇函数f（x）在区间[a，b]（0＜a＜b）上是增函数，且最小值为2，那么f（x）在区间[－b，－a]上是（　　）．
    A

    增函数且最小值为－2

    B

    增函数且最大值为－2

    C

    减函数且最小值为－2

    D

    减函数且最大值为－2


    正确答案： D
    解析：
    由于奇函数的图象关于坐标原点对称，借助图象（可作一草图，略），可知函数在原点两边定义域对称的范围内，其函数增减性一致．因此f（x）在[－b，－a]上也是增函数．而原点右边某一区间上的最大（小）值C，对称过去应为原点左边相应区间的最小（大）值－C．

  • 第12题：

    单选题
    如图所示的周期为T的三角波信号，在用傅氏级数分析周期信号时，对系数a 0、a n和b n正确的判断是（）。
    A

    该信号是奇函数且在一个周期的平均值为零，所以傅立叶系数a 0和b n是零

    B

    该信号是偶函数且在一个周期的平均值不为零，所以傅立叶系数a 0和a n不是零

    C

    该信号是奇函数且在一个周期的平均值不为零，所以傅立叶系数a 0和b n不是零

    D

    该信号是偶函数且在一个周期的平均值为零，所以傅立叶系数a 0和b n是零


    正确答案： C
    解析： 从信号的波形图可以看出信号关于y轴对称，所以是偶函数，信号取值均大于0，所以在一个周期的平均值不为零。傅立叶系数a 0和b n分别表示信号的平均分量和谐波分量，三角波是高次谐波信号，所以傅立叶系数a 0和b n不是零。

  • 第13题：

    设函数 f (x)在（-∞，+∞）上是偶函数，且在（0，+∞）内有 f ' (x) >0， f '' (x) >0，
    则在（- ∞ ，0）内必有：
    （A） f ' > 0, f '' > 0 （B） f ' 0
    （C） f ' > 0, f ''


    答案：B
    解析：
    解：选 B。
    偶函数的导数是奇函数，奇函数的导数是偶函数。
    f (x)是偶函数，则 f '(x)是奇函数，当x > 0时， f '(x) > 0，则x f '(x)是奇函数，则 f ''(x)是奇函数，当x > 0时， f '(x) > 0，则x 0；
    点评：偶函数的导数是奇函数，奇函数的导数是偶函数。

  • 第14题：

    定义在R上的奇函数．f(x)，满足f(x+4)=-f(x)，且在[0，2]为增函数，则有( )。

    A.f(19)＞f(24)＞f(-25)
    B.f(24)＞f(19)＞f(-25)
    C.f(-25)＞f(19)＞f(24)
    D.f(-25)＞f(24)＞f(19)

    答案：A
    解析：
    因为f(x+4)=-f(x),f(x+8)=f(x+4+4)=f(x)，所以f(19)=f(3+2×8)=f(3)=f(-1+4)=-f(-1)=f(1),f(24)=f(3×8)=f(0),f(-25)=f(-1-8×3)=f(-1)，又因为函数是奇函数，且在[0，2]上为增函数，故其在[-2，2] 上为增函数，所以f(-25)＜f(24)＜f(19)，故A正确。

  • 第15题：

    若f(x)为偶函数，且在(0，＋∞)为增函数，则下列不等式成立的是（　　）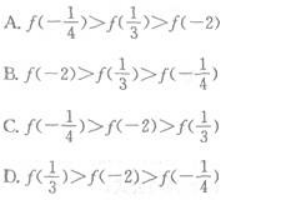


    答案：B
    解析：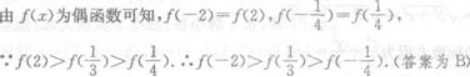

  • 第16题：

    设函数f（x）是连续且单调增加的奇函数，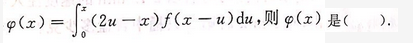

    A.单调增加的奇函数
    B.单调减少的偶函数
    C.单调增加的偶函数
    D.单调减少的偶函数

    答案：B
    解析：

  • 第17题：

    设函数f(x)在(-∞，+∞)上是偶函数，且在(0，+∞)内有f'(x)＞0， f''(x)＞0，则在(-∞，0)内必有：

    A. f'(x)＞0， f''(x)＞0
    B.f'(x)＜0， f''(x)＞0
    C. f'(x)＞0， f''(x)＜0
    D. f'(x)＜0， f''(x)＜0

    答案：B
    解析：
    提示 已知f(x)在(-∞，+∞)上是偶函数，函数图像关于y轴对称，已知函数在(0，+∞)，f'(x)＞0， f''(x)＞0，表明在(0，+∞)上函数图像为单增且凹向，由对称性可知，f(x)在(-∞，0)单减且凹向，所以f'(x)＜0， f''(x)＞0。

  • 第18题：

    如图所示的周期为T的三角波信号，在用傅氏级数分析周期信号时，系数a0、an和bn判断正确的是：


    A.该信号是奇函数且在一个周期的平均值为零，所以傅立叶系数a0和bn是零
    B.该信号是偶函数且在一个周期的平均值不为零，所以傅立叶系数a0和an不是零
    C.该信号是奇函数且在一个周期的平均值不为零，所以傅立叶系数a0和bn不是零
    D.该信号是偶函数且在一个周期的平均值为零，所以傅立叶系数a0和bn是零

    答案：B
    解析：
    提示：周期信号的傅氏级数分析。

  • 第19题：

    设函数f(x)在(-∞,+∞)上是偶函数，且在(0,+∞)内有f'(x)>0,f''(x)>0,则在(-∞,0)内必有（ ）。
    A. f'(x)>0,f''(x)>0 B. f(x) 0
    C. f'(x)>0,f''(x)


    答案：B
    解析：
    提示：f(x)在(-∞,+∞)上是偶函数，f'(x)在(-∞,+∞)在上是奇函数，f''(x)在(-∞,+∞)在上是偶函数，故应选B。

  • 第20题：

    若函数f(x)=(k-1)ax- ax (a＞0且α≠1)在R上既是奇函数，又是减函数，则g(x)=loga (x+k)的图象是( )。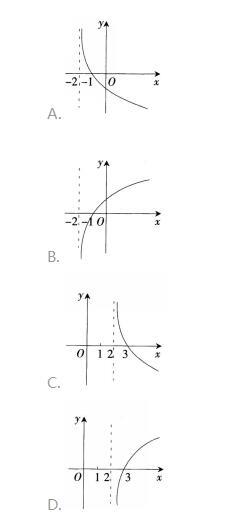


    答案：A
    解析：
    函数f(x)是奇函数，则有f(0)=(k-1)-1=0，得k=2.f(x)=ax-a-x。又f(x)在R上是减函数，则有0

  • 第21题：

    设f（x）在（-a，a）（a＞0）上连续，F（x）是f（x）的一个原函数，则当f（x）是奇函数时，下面结论正确的是（）。

    • A、F（x）是偶函数
    • B、F（x）是奇函数
    • C、F（x）可能是奇函数，也可能是偶函数
    • D、F（x）是否为奇函数不能确定

    正确答案:A

  • 第22题：

    单选题
    若f（x）是在（－l，l）（l＞1）内的不恒为0的可导奇函数，则f′（x）（　　）。
    A

    必为（－l，l）内的奇函数

    B

    必为（－l，l）内的偶函数

    C

    必为（－l，l）内的非奇非偶函数

    D

    可能是奇函数也可能是偶函数


    正确答案： C
    解析：
    f（x）为不恒为0的可导奇函数，则f（－x）＝－f（x），两端对x求导，得f′（－x）（－1）＝－f′（x），即f′（－x）＝f′（x），故f′（x）必为（－l，l）内的偶函数。

  • 第23题：

    单选题
    设在区间（－∞，＋∞）内函数f（x）＞0，且当k为大于0的常数时有f（x＋k）＝1/f（x）则在区间（－∞，＋∞）内函数f（x）是（　　）。
    A

    奇函数

    B

    偶函数

    C

    周期函数

    D

    单调函数


    正确答案： D
    解析：
    对该函数由f（x＋2k）＝1/f（x＋k）＝f（x），故f（x）是周期函数。

相关内容