以χ2-3χ-1=0的两个根的平方为根的一元二次方程是( )A.χ2-11χ+10 B.χ2+χ-11=0 C.χ2-11χ-1=0 D.χ2+χ+1=0

题目
以χ2-3χ-1=0的两个根的平方为根的一元二次方程是( )

A.χ2-11χ+10
B.χ2+χ-11=0
C.χ2-11χ-1=0
D.χ2+χ+1=0
相似考题

1.若两个变量存在负线性相关关系，则建立一元线性回归方程得到的判定系数R2的取值范围是（ ）。A．[0，1]B．[-1，0]C．[-1，1]D．小于0的任意数

2.● 某有限自动机的状态图如下图所示，其特点是 （31） 。（31）A. 仅识别以0开始以1结尾的0、1串B. 仅识别含有3个0的0、1串C. 仅识别含有偶数个1的0、1串D. 仅识别以0开始以1结尾且0与1交错出现的0、1串

3.函数Int(Rnd(0)*10)的取值范围是______。A．(0，10)B．(0，1)C．(1，10)D．(1，2)

4.图8-2为一个DFA的状态转换图，与其等价的正规表达式是(31)，在图中状态(32)是可以合并的状态。A．(0|1)*11(0*1*)*B．(0|1)*110*|1*C．(0*1*)11(0|1)*D．(0*|1*)*11(0*|1*)

参考答案和解析
答案：A
解析：
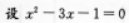【考情点拨】本题主要考查的知识点为根与系数的关系． 【应试指导】的两根分别为χ1，χ2，则由根与系数的关系得χ1+χ2=3，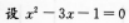
又所求方程的两根为
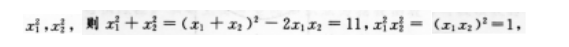
∴所求方程为χ2-11χ+1=0．
更多“以χ2-3χ-1=0的两个根的平方为根的一元二次方程是( )A.χ2-11χ+10 B.χ2+χ-11=0 C.χ2-11χ-1=0 D.χ2+χ+1=0”相关问题

  • 第1题：

    已知命题，则所有使G取真值1的解释是(65)。

    A．(0，0，0)，(0，0，1)，(1，0，0)

    B．(1，0，0)，(1，0，1)，(1，1，0)

    C．(0,1,0),(1,0,1),(0,0,1)

    D．(0,0,1),(1,0,1),(1,l,1)


    正确答案：B
    解析：

  • 第2题：

    中冲穴的定位是

    A.中指尺侧指甲根角旁0. 1寸
    B.中指桡侧指甲根角旁0. 1寸
    C.无名指桡侧指甲根角旁0. 1寸
    D.中指尖端的中央
    E.无名指尖端的中央

    答案：D
    解析：
    中冲
    【定位】在手指，中指末端最高点。

  • 第3题：

    设Ω是由锥面x^2+(y-2)^2=(1-z)^2(0≤x≤1)与平面z=0围成的锥体，求Ω的形心坐标.


    答案：
    解析：

  • 第4题：




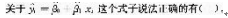
    A.这是Y对X的一元线性回归方程
    B.式中β0、β1是两个未知常数
    C.β1表示直线在Y轴上的截距
    D.β0为直线的斜率
    E.β0、β1一旦确定这条直线也就唯一确定了

    答案：A,B,E
    解析：
    本题考查Y对x的一元线性回归方程。选项CD说法反了，岛表示直线在y轴上的截距，



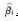
    为直线的斜率。

  • 第5题：

    已知两数的等差中项为10，等比中项为8，则以这两数为根的一元二次方程是（）

    A.x2+10x+8=0
    B.x2-10x+64=0
    C.x2-20x+8=0
    D.x2-20x+64=0

    答案：D
    解析：

  • 第6题：

    如图所示电路中，Q1、Q2的原始状态为“11”当送入两个脉冲后的新状态为: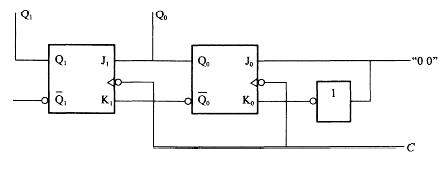


    A. “0 0 ”
    B. “0 1”
    C. “11”
    D. “10”

    答案：A
    解析：
    提示 该电路为时序逻辑电路，具有移位、存贮功能、两个脉冲过后的新状态为Q1Q0=00。

  • 第7题：

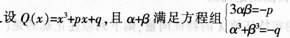    (1)证明α+β是Q（χ）=0的根；(3分)
    (2)写出以α3和β3为根的一元二次方程。(4分)


    答案：
    解析：
    (1)因为α3+β3=-q，所以

  • 第8题：

    χ2值的取值范围为（）

    • A、-∞<χ2<+∞
    • B、0≤χ2≤+∞
    • C、χ2≤1
    • D、-∞≤χ2≤0
    • E、χ2≥1

    正确答案:B

  • 第9题：

    具有两个输入的异或非门（NXOR）是最简单的数字逻辑电路之一。如果两个输入信号组合分别为00、01、10、11，对应的输出信号应为（）

    • A、0、1、1、0
    • B、0、1、1、1
    • C、1、1、0、0
    • D、1、0、0、1

    正确答案:D

  • 第10题：

    [Co（NH3）6]2+、[Co（NH3）6]3+的成单电子数分别是（）

    • A、3和4
    • B、1和4
    • C、3和0
    • D、1和0
    • E、2和0

    正确答案:C

  • 第11题：

    单选题
    已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是（　　）。
    A

    k（0，1，－1，－1）T＋（1，1，0，2）T

    B

    k（0，1，－1，－1）T＋（1，1，0，2）T/2

    C

    k（1，1，0，2）T＋（0，1，－1，－1）T

    D

    k（1，1，0，2）T＋（0，1，－1，－1）T/2


    正确答案： D
    解析：
    由Aα(→)1＝b(→)，Aα(→)2＝b(→)，故A[（α(→)1＋α(→)2）/2]＝b(→)，则（α(→)1＋α(→)2）/2是方程组AX(→)＝b(→)的特解。
    又r（A）＝3，故四元齐次方程组AX(→)＝b(→)的基础解系只含有一个解向量。由α(→)1，α(→)3是AX(→)＝b(→)的解向量，知α(→)1－α(→)3是齐次方程组AX(→)＝0(→)的解，而α(→)1－α(→)3＝（α(→)1＋α(→)2）－（α(→)2＋α(→)3）＝（0，1，－1，－1）T，故AX(→)＝b(→)的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。

  • 第12题：

    单选题
    已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是（　　）。
    A

    k（0，1，1，1）T＋（1，1，0，2）T/2

    B

    k（0，1，－1，－1）T＋（1，1，0，2）T/2

    C

    k（0，1，1，－1）T＋（1，1，0，2）T/2

    D

    k（0，1，－1，1）T＋（1，1，0，2）T/2


    正确答案： C
    解析：
    由Aα(→)1＝b(→)，Aα(→)2＝b(→)，故A[（α(→)1＋α(→)2）/2]＝b(→)，则（α(→)1＋α(→)2）/2是方程组AX(→)＝b(→)的特解。又r（A）＝3，故四元齐次方程组AX(→)＝b(→)的基础解系只含有一个解向量。由α(→)1，α(→)3是AX(→)＝b(→)的解向量，知α(→)1－α(→)3是齐次方程组AX(→)＝0(→)的解，而α(→)1－α(→)3＝（α(→)1＋α(→)2）－（α(→)2＋α(→)3）＝（0，1，－1，－1）T，故AX(→)＝b(→)的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。

  • 第13题：

    一元二次方程x2+x-2=0 的两根之积是（ ）

    A．-1

    B．-2

    C．1

    D．2


    正确答案：B

  • 第14题：

    厉兑穴位于

    A.第2趾内侧趾甲根角旁约0. 1寸
    B.第2趾外侧趾甲根角旁约0. 1寸
    C.第4趾内侧趾甲根角旁约0. 1寸
    D.第4趾外侧趾甲根角旁约0. 1寸
    E.第3趾内侧趾甲根角旁约0. 1寸

    答案：B
    解析：
    厉兑
    【定位】在足趾，第2趾末节外侧，趾甲根角侧后方0.1寸（指寸）。

  • 第15题：

    下列回归模型中，属于一元线性回归模型的是（）。

    A.Y = β0 + β1 X1 + β2X2+ε
    B.Y = β0 + β1 X 1+ β1 X 21+ε
    C.Y = β0X 1β1 X 2β2+ε
    D.Y = β0 + β1 X + ε

    答案：D
    解析：
    回归模型可以用描述因变量Y如何依赖自变量X和误差项ε的方程来表示。只涉及一个自变量的一元线性回归模型可以表示为：
    Y=β0+β1X+ε
    式中β0和β1为模型的参数
    y是x的线性函数(β0+β1X)加上误差项ε。@##

  • 第16题：

    过点A(1,-1)，B(-1,1)且圆心在直线x+y-2=0上的圆的方程是（ ）。

    A.(x-3)2+(y+1)2=4
    B.(x+3)2+(y-1)2=4
    C.(x-1)2+(y-1)2=4
    D.(x+1)2+(y+1)2=4

    答案：C
    解析：

  • 第17题：


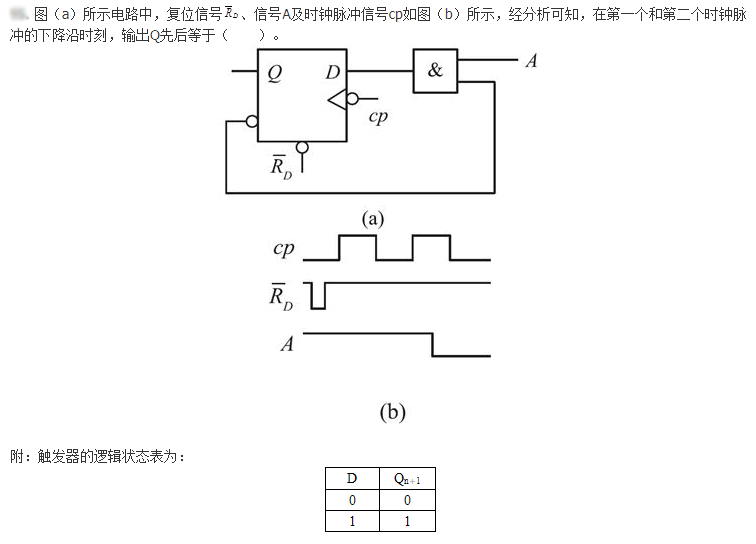    A． 0　0
    B． 0　1
    C． 1　0
    D． 1　1

    答案：C
    解析：

  • 第18题：


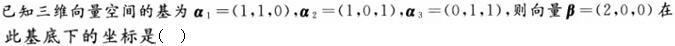    A.（2，0，0）
    B.（1，1，-1）
    C.（1，0，-1）
    D.（0，0，0）

    答案：B
    解析：

  • 第19题：

    方程χ5-1=0的5个根在复平面上是一个正五边形的顶点．
    (1)求方程χ4+χ3+χ2+χ+1=0的四个复根中落在第一象限的那个根，要求用根式表达。(提示：做变量替换z=χ+1/χ)
    (2)利用(1)的结论，计算单位圆的内接正五边形的边长。


    答案：
    解析：

  • 第20题：

    具有两个输入的异或门（XOR）是最简单的数字逻辑电路之一。如果两个输入信号组合分别为00、01、10、11，对应的输出信号应为（）

    • A、1、0、1、0
    • B、0、1、0、1
    • C、0、1、1、1
    • D、0、1、1、0

    正确答案:D

  • 第21题：

    具有两个输入的与门（AND）是最简单的数字逻辑电路之一。如果两个输入信号的组合分别为00、01、10、11，对应的输出信号应为（）

    • A、0、0、0、1
    • B、0、1、1、1
    • C、0、1、0、1
    • D、1、0、1、0

    正确答案:A

  • 第22题：

    单选题
    设α1，α2，α3，α4是4维非零列向量组，A=（α1，α2，α3，α4），A*是A的伴随矩阵，已知方程组AX=0的基础解系为k（1，0，2，0）T，则方程组A*X=0的基础解系为（　　）.
    A

    α1，α2，α3

    B

    α1+α2，α2+α3，3α3

    C

    α2，α3，α4

    D

    α1+α2，α2+α3，α3+α4，α4+α1


    正确答案： D
    解析：
    由AX=0的基础解系仅含有一个解向量，知r（A）=4-1=3，所以r（A*）=1，则AX=0A*X=0的基础解系含三个解向量．
    又（α1，α2，α3，α4）（1，0，2，0）T=0，即α1+2α3=0，知（α1，α3）线性相关，所以方程组A*X=0的基础解系为α2，α3，α4．

  • 第23题：

    单选题
    χ2值的取值范围为（）
    A

    -∞<χ2<+∞

    B

    0≤χ2≤+∞

    C

    χ2≤1

    D

    -∞≤χ2≤0

    E

    χ2≥1


    正确答案： E
    解析： 根据分布的图形或χ2的基本公式可以判断χ2值一定是大于等于零且没有上界的，故应选B。

相关内容