[0402]设甲：四边形ABCD是平行四边形，乙：四边形ABCD是正方形，则（　　）A.甲是乙的充分条件，但不是乙的必要条件 B.甲是乙的必要条件，但不是乙的充分条件 C.甲是乙的充分必要条件 D.甲不是乙的充分条件，也不是乙的必要条件

题目
[0402]设甲：四边形ABCD是平行四边形，乙：四边形ABCD是正方形，则（　　）

A.甲是乙的充分条件，但不是乙的必要条件
B.甲是乙的必要条件，但不是乙的充分条件
C.甲是乙的充分必要条件
D.甲不是乙的充分条件，也不是乙的必要条件
相似考题

1.平行四边形ABCD的周长是28cm，CD－AD＝2cm，则AB的长度是（ ）。A．8cmB．6cmC．7cmD．9cm

2.长方形是特殊的（ ）。A 正方形B 平行四边形C 梯形D 四边形

3.在平行四边形ABCD中，∠DAB＝60°，AB＝15cm．已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F，⊙O在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止，试求⊙O滚过的路程．

4.四个角相等的四边形是（ ）。A 梯形B 长方形C 平行四边形D 正方形

参考答案和解析
答案：B
解析：
更多“[0402]设甲：四边形ABCD是平行四边形，乙：四边形ABCD是正方形，则（　　）”相关问题

  • 第1题：

    如图，甲、乙、丙、丁四个长方形拼成正方形 EFGH，中间阴影为正方形。已知，甲、乙、丙、丁四个长方形面积的和是 32cm2，四边形 ABCD 的面积是 20cm2。问甲、乙、丙、丁四个长方形周长的总和

    是( )。（图略）

    A.32cm

    B.56cm

    C.48cm

    D.68cm


    正确答案：C

  • 第2题：

    喷头组合形式有正方形 （） 、 平行四边形。


    正确答案：矩形

  • 第3题：

    在平行四边形ABCD中，∠DAB=60，AB=15cm，已知圆O的半径等于3cm，AB，AD分别与圆O相切于点E，F.圆0在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止．试求圆O滚过的路程．


    答案：
    解析：

  • 第4题：

    如图，平面四边形ABCD中，AB=2，BC=4，CD=5，DA=3，
    (1)若∠B与∠D互补，求AC2的值；
    (2)求平面四边形ABCD面积的最大值。


    答案：
    解析：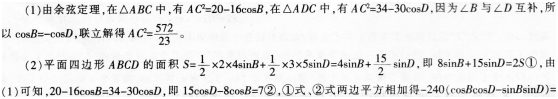

  • 第5题：

    如图，已知图中四边形两条边的长度和三个角的度数，四边形ABCD的面积是______cm2。


    答案：
    解析：
    24。解析：延长AD和BC交于点E，则得到两个等腰直角三角形△ABE和△DCE，四边形ABCD

  • 第6题：

    如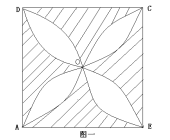，四边形ABCD是边长为1的正方形，弧AOB，BOC，COD，DOA均为半圆，则阴影部分的面积为



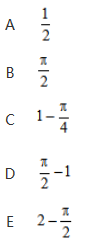    答案：E
    解析：

  • 第7题：

    初中数学《平行四边形的判定》

    一、考题回顾



    二、考题解析
    【教学过程】
    (一)引入新课
    提出问题：平行四边形的定义是什么?平行四边形有什么性质?我们可以说怎么样的一个图形是平行四边形呢?除定义之外还有没有其它的方法来判定一个四边形是平行四边形呢?
    由此引出今天学习的内容是《平行四边形的判定》。
    (二)探索新知
    通过前面的学习，我们知道，平行四边形的对边相等，对角相等，对角线互相平分。那么反过来，对边相等或对角线互相平分的四边形是不是平行四边形呢?下面我们就来验证一下。
    实验一：取两长两短的四根木条用小钉铰在一起，做成一个四边形，如果等长的木条成为对边，那么无论如何转动这个四边形，它的形状都是平行四边形;
    实验二：取两根长短不一的细木条，将它们的中点重叠，并用小钉钉在一起，用橡皮筋连接木条的顶点，做成一个四边形。转动两根木条，这个四边形是平行四边形。
    引导学生归纳得出结论：
    两组对边分别相等的四边形是平行四边形;
    两组对角分别相等的四边形是平行四边形;
    对角线互相平分的四边形是平行四边形。
    提问学生：你能根据平行四边形的定义证明它们吗?
    引导学生以“对角线互相平分的四边形是平行四边形”为例，通过三角形全等进行证明。明确平行四边形的判定定理与相应的性质定理互为逆定理。
    提问学生：求证四边形ABCD是平行四边形，说一说有哪些证明方法?
    预设：可以利用定义，或证明两组对边分别相等，或两组对角分别相等。
    继续提问：思考两组对边分别平行或相等的四边形是平行四边形，如果只考虑四边形的一组对边，它们满足什么条件时这个四边形能成为平行四边形呢?
    学生活动：组织学生前后桌四人一组进行讨论，教师巡视指导。引导学生猜想一组对边平行且相等的四边形是平行四边形，并进行证明。
    通过充分讨论和分享，结合学生的回答，教师明确：平行四边形判定的另一种方法，即一组对边平行且相等的四边形是平行四边形。
    提问学生：现在你有多少种判定一个四边形是平行四边形的方法?
    引导学生回顾平行四边形判定的四种方法。
    (三)课堂练习
    基础题：练习题1，引导学生利用平行四边形判定的四种方法进行证明。
    提升题：练习题2，解决生活实际问题。
    (四)小结作业
    提问：今天有什么收获?
    引导学生回顾：本节课学习了平行四边形判定的四种方法。
    课后梯度作业：必做题和选做题。
    【板书设计】



    1.平行四边形的判定定理都有哪些?
    2.为什么要学习平行四边形的判定?


    答案：
    解析：
    1.
    两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形。
    2.
    平行四边形的判定是对前面所学全等三角形和平行四边形性质的一个回顾和延伸，又是后续学习特殊的平行四边形的基础，同时它还进一步培养学生的简单的推理能力、图形迁移能力、观察能力、合情推理能力，使学生学会将平行四边形的问题转化为三角形的问题，渗透化归思想。

  • 第8题：

    如图8，四边形ABCD内接于⊙O，若∠BCD=130o，则∠BOD=_______°。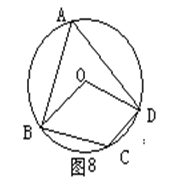


    答案：
    解析：
    100

  • 第9题：

    下列说法中，不正确的是（　　）。

    A.两组对边分别相等的四边形是平行四边形
    B.平行四边形的对角线互相平分
    C.平行四边形的对边相等
    D.对角线相等的四边形是平行四边形

    答案：D
    解析：
    对于A项，两组对边分别相等的四边形是平行四边形，说法正确；对于B项，平行四边形的对角线互相平分，说法正确；对于C项，平行四边形的对边相等，说法正确；对于D项，对角线相等的四边形是平行四边形，说法错误，例如，等腰梯形对角线相等，但不是平行四边形。故选D。

  • 第10题：

    下列关于特殊四边形的表述中，正确的有（）

    • A、一组对边平行且相等的四边形是平行四边形
    • B、四条边都相等的四边形是矩形
    • C、对角线互相垂直的四边形是菱形
    • D、正方形既是矩形又是菱形

    正确答案:A,D

  • 第11题：

    只有一组对边平行的四边形是（）。

    • A、平行四边形
    • B、长方形
    • C、正方形
    • D、梯形

    正确答案:D

  • 第12题：

    单选题
    只有一组对边平行的四边形是（）。
    A

    平行四边形

    B

    长方形

    C

    正方形

    D

    梯形


    正确答案： A
    解析： 暂无解析

  • 第13题：

    平行四边形中，已知AB、BC及其夹角∠ B（∠ B是锐角），能求出平行四边形ABCD的面积S吗？如果能，写出用AB，BC及其夹角∠ B表示S的式子。


     

    S=BC×AB×sinB


  • 第14题：

    如下图，平行四边形ABCD的对角线相交于点O，直线EF经过点O，分别与AB，CD的延长线交于点E，F．求证：四边形AECF是平行四边形．



    答案：
    解析：
    证明：如右图所示，∵四边形ABCD为平行四边形，∴BO=DO，



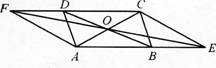
    又∵AB∥CD，∴∠FDO=∠EB0

  • 第15题：

    若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD一定是( )。

    A.对角线相互垂直的四边形
    B.矩形
    C.对角线相等的四边形
    D.菱形

    答案：A
    解析：
    对角线相互垂直的四边形顺次连接各边中点所得四边形是矩形，对角线相等的四边形顺次连接各边中点所得四边形是菱形。

  • 第16题：

    如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E,且AD=14，DC=9，则BE/EC的值为()。

    A.1/3
    B.4/9
    C.5/9
    D.2/3

    答案：C
    解析：
    AD∥BC，则∠ADE=∠DEC，又∠ADE=∠CDE，所以△CDE为等腰三角形，EC=CD=9，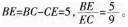

  • 第17题：

    平行四边形ABCD如右图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：

    A.2︰7
    B.3︰13
    C.4︰19
    D.5︰24

    答案：D
    解析：
    第一步，本题考查几何问题，属于平面几何类，用赋值法解题。
    第二步，题干没给出具体数值，可以采用赋值法解题。赋值AB=3，平行四边形ABCD的高为4，则AE=1；由于△AEF相似于△CDF，则两个三角形的高之比为AE：DC=1︰3，可知△AEF的高为
    4*1/4=1。△ABG与△CDG全等，则△ABG的高为4÷2=2。
    第三步，四边形BEFG面积=△ABG面积-△AEF面积=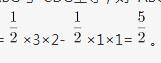

    四边形ABCD面积=3×4=12，两者之比为 ︰12=5︰24。
    因此，选择D选项。

  • 第18题：

    如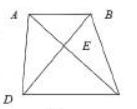，在四边形ABCD中，AB//CD，AB与CD的边长分别为4和8，若ABE的面积为4，则四边形ABCD的面积为（ ）

    A.24
    B.30
    C.32
    D.36
    E.40

    答案：D
    解析：

  • 第19题：

    如图7，在四边形ABCD中，AD∥BC，要使四边形ABCD为平行四边形，则应添加的条件是__________（添加一个条件即可）。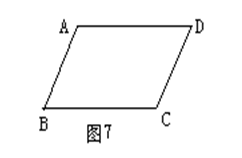


    答案：
    解析：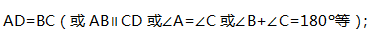

  • 第20题：

    如图，平行四边形ABCD的面积是54平方厘米，点E、F、G分别是平行四边形ABCD边上的中点，H为AD边上的任意一点，则阴影部分的面积为（ ）平方厘米。


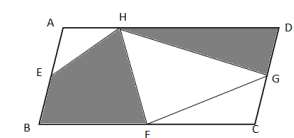    A. 27
    B. 28
    C. 32
    D. 36

    答案：A
    解析：
    方法一：如图所示，由于H为AD边上的任意一点，假设H点与A点重叠，则左边阴影为三角形ABF，其面积为三角形ABC的一半；右边阴影为三角形ADG，其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半，平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。



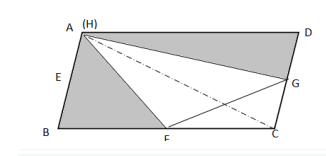
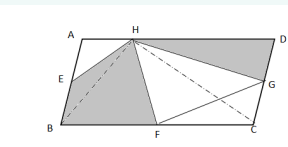
    方法二：如图所示，连接BH和CH，由于点E、F、G分别是平行四边形ABCD边上的中点，则三角形AEH和BEH相等，三角形BFH和CFH相等，三角形CGH和DGH相等，因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米，则阴影部分面积为27平方厘米。因此，本题答案为A选项。

  • 第21题：

    如图，平行四边形ABCD，∠ADC的角平分线DE交BC于E，且AD=14，DC=9，




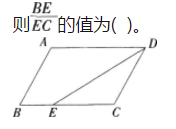
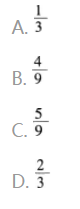    答案：C
    解析：

  • 第22题：

    理论示功图中，在一个冲次中悬点做的（）为平行四边形ABCD的面积。

    • A、负功
    • B、净功
    • C、功
    • D、冲程

    正确答案:B

  • 第23题：

    单选题
    圆内接四边形ABCD中，已知∠A＝70°，则∠C＝（　　）．
    A

    20°

    B

    30°

    C

    70°

    D

    110°


    正确答案： D
    解析：
    圆内接四边形的对角互补，所以∠C＝110°．

相关内容