若A（-3,5），B（-5,-3），则线段AB中点的坐标为（　　）A.（4,-1） B.（-4,1） C.（-2,4） D.（-1,2）

题目

若A（-3,5），B（-5,-3），则线段AB中点的坐标为（　　）

A.（4,-1）
B.（-4,1）
C.（-2,4）
D.（-1,2）

相似考题

1.若直线AB的坐标方位角为123°18′21″，则直线BA的坐标方位角为()。

2.已知直线AB的坐标方向角为185°,则直线BA的坐标方位角为()A、95°B、275°C、5°D、185°

3.若AB方向X坐标增量小于零，Y坐标增量小于零,则直线AB方向在第三象限内。此题为判断题(对，错)。

4.若已知两点的坐标为A(100，100)和B(150，50)，则直线AB的坐标方位角为()。

更多“若A（-3,5），B（-5,-3），则线段AB中点的坐标为（　　）”相关问题

第1题：

已知过点（0，4），斜率为-1的直线l与抛物线C：y2—2px（b>；0）交于A，B两点．
（I）求C的顶点到2的距离；
（Ⅱ）若线段AB中点的横坐标为6，求C的焦点坐标．

正确答案：
第2题：

已知直线 AB 两端点的坐标为 A(2,3),B(5,6).写出使直线 AB 以坐标原点为中心顺时针旋转 90 的变换矩阵，并求出变换后直线 AB 的坐标矩阵。

参考答案：
(1)AB 的齐次坐标矩阵为:
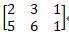
(2)绕原点顺时针旋转 90°的变换矩阵为：
(3)变换后直线 AB 的坐标矩阵为:
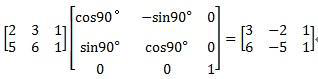
第3题：

建立平面直角坐标系，并描出下列各点：
A（1， 1）， B（5， 1）， C（3， 3）， D（-3， 3）， E（1， -2）， F（1， 4），G（3， 2）， H（3， -2），I（-1， -1）， J（-1， 1）。
连接AB，CD，EF，GH，IJ，找出它们中点的坐标，将上述中点的横坐标和纵坐标分别与对应线段的两个端点的横坐标和纵坐标进行比较，你发现它们之间有什么关系？写出你的发现，并与其他同学进行交流。
第4题：

include<iostream>
include<string>
using namespace std;
template <class T>
T Max(T a,T b)
{return a>b? a:b;}
T Mix(T a,T b)
{return a>b? b:a;}
void main()
{
cout<<"Max(3,5)"<<Max<double>(3,5)<<endl;
cout<<"Mix(3,5)"<<Mix<int>(3,5)<<endl;
}

正确答案：
TMin(Ta,Tb)每个函数模板前面都要进行声明。在TMin(Ta,Tb)前面添加一行：template<classT>。
第5题：

⑵在复平面内，复数6+5i, -2+3i 对应的点分别为A,B.若C为线段AB的中点，则点C对应的复数是
（A）4+8i
（B）8+2i
（C）2+4i
（D）4+i

正确答案：C
第6题：

已知A(-1，-l)，B(3，7)两点，则线段AB的垂直平分线方程为__________.

答案：
解析：
【答案】χ+2y=0 【考情点拨】本题主要考查的知识点为线段的垂直平分线．
【应试指导】设线段的垂直平分线上任一点为P(χ，y)，则
即
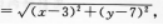
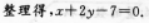
第7题：

在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则( )。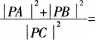

A、2
B、4
C、5
D、10

答案：D
解析：
本题主要考查两点问的距离公式，以及坐标法这一重要的解题方法和数形结合的数学思
第8题：

设抛物线y2=2px(p>0)焦点为F，点A坐标为(0，2)，若线段FA的中点B在抛物线上，则B到该抛物线准线距离为__________。

答案：
解析：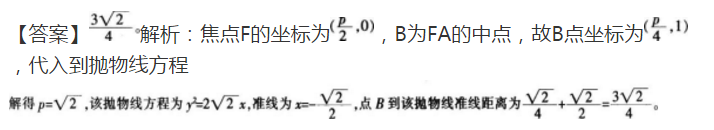
第9题：

线段A（-6，1）、B（8，-3）的中点坐标为（）。
- A、（1，－1）
- B、（-7，-2）
- C、（1，-2）
- D、（-7，-1）
正确答案:A
第10题：

填空题
若已知两点的坐标为A（100，100）和B（150，50），则直线AB的坐标方位角为（）。

正确答案： 315°
解析：暂无解析
第11题：

填空题
若直线AB的坐标方位角为123°18′21″，则直线BA的坐标方位角为（）。

正确答案： 303°18′21″
解析：暂无解析
第12题：

单选题
线段AB平行于y轴，且|AB|＝6，若点A的坐标为（3，2），则点B的坐标是（　　）．
A
（9，2）或（－3，2）
B
（3，8）
C
（3，4）
D
（3，8）或（3，－4）

正确答案： A
解析：
∵AB∥y轴，∴B点坐标可写为（3，y），又∵|AB|＝6, ∴|y－2|＝6，y＝8或y＝－4．故B点坐标是（3，8）或（3，－4）．
第13题：

线段A(-6，1)、B(8，-3)的中点坐标为( )。
A.(-7,-1)
B.(-7,-2)
C.(1,-2)
D.(1,-1)

正确答案：D
第14题：

在直角坐标系中，将坐标是（2，0），（2，2），（0，2），（0，3），（2，5），（3，5），（2，2），（5，3），（5，2），（3，0），（2，0）的点用线段依次连接起来形成一个图案。
（1）每个点的横坐标保持不变，纵坐标变成原来的½，再将所得的各个点用线段依次连接起来，所得的图案与原图案相比有什么变化。
（2）纵坐标保持不变，横坐标分别加3呢？
（3）横坐标保持不变，纵坐标分别加3呢？
（4）纵坐标保持不变，横坐标分别乘-1呢？
（5）纵、横坐标分别变为原来的2倍呢？
（6）横坐标保持不变，纵坐标分别乘以-1呢？
第15题：

已知A,B是抛物线y2=4x上的两个动点,且|AB|=3,则当AB的中点M到y轴的距离最短时,点M的横坐标是____.

参考答案B9/16
第16题：

在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（）。
A．2.5
B．5
C．10
D．15

正确答案：A
分析：由D、E分别是边AB、AC的中点可知，DE是ABC的中位线，根据中位线定理可知，DE＝BC＝2.5。
涉及知识点：中位线
点评：本题考查了中位线的性质，三角形的中位线是指连接三角形两边中点的线段，中位线的特征是平行于第三边且等于第三边的一半。
推荐指数：★★
第17题：

已知点A的坐标为(2,－1),AB=4,AB∥X轴,则B点的坐标为_________

正确答案：
(－2，－1)，（6，－1）
第18题：

C是线段AB上一点，D是线段CB的中点，已知图中所有线段的长度之和为23，线段 AC和线段CB的长度都是正整数,那么线段4C的长度为：

A.2
B.3
C.5
D.7

答案：B
解析：
。解析是Cfl的中点’CD=DB=1/2CB。所有线段长度之和=4C+AD+AB+CD+CB+DB=AC+(AC+
第19题：

如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。

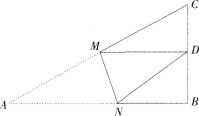答案：
解析：
第20题：

已知一次函数的图像过点（3，5）与（-4，-9），则该函数的图像与y轴交点的坐标为（0，-1）。

正确答案:正确
第21题：

已知线段AB的水平距离为200米，线段AB的方位角为133°10′22″，则线段AB的X轴方向的坐标增量为（）
- A、+145.859
- B、-145.859
- C、+136.840
- D、-136.840
正确答案:D
第22题：

判断题
已知一次函数的图像过点（3，5）与（-4，-9），则该函数的图像与y轴交点的坐标为（0，-1）。
A
对
B
错

正确答案：错
解析：暂无解析
第23题：

填空题
已知点A（－1，1），B（3，5），x轴上一点M到A，B的距离相等，则点M的坐标是____．

正确答案： (4,0)
解析：
设M（x，0），则得方程（x＋1）²＋1²＝（x－3）²＋5²，解此方程，得x＝4．

若A（-3,5），B（-5,-3），则线段AB中点的坐标为（ ）A.（4,-1） B.（-4,1） C.（-2,4） D.（-1,2）

题目

相似考题

更多“若A（-3,5），B（-5,-3），则线段AB中点的坐标为（ ）”相关问题

相关内容

若A（-3,5），B（-5,-3），则线段AB中点的坐标为（　　）A.（4,-1） B.（-4,1） C.（-2,4） D.（-1,2）

更多“若A（-3,5），B（-5,-3），则线段AB中点的坐标为（　　）”相关问题