点（－3，2），（a,a+1）在函数y=kx－1的图像上，则k= ,a=
题目
点（－3，2），（a,a+1）在函数y=kx－1的图像上，则k= ,a=
相似考题
更多“点(－3,2),(a,a＋1)在函数y=kx－1的图像上,则k=,a= ”相关问题
-
第1题：
已知一次函数y-2x+b的图像经过点（-2，1），则该图像也经过点 （ ）
A.（1，7）
B.（1，-3）
C.（1，5）
D.（1，-l）
正确答案：A
本题主要考查的知识点为一次函数．【应试指导】因为一次函数y=2x+b的图像过点(-2，1)，所以，l=2×(-2)+b，b=5，即y=2z+5．结合选项，当x=1时，y=7，故本题选A． -
第2题：
填空: 对于函数y=3／x,当 x>0时,y___0,这部分图像在第_____象限;对于函数y=－3填空： 对于函数y=3/x，当x>0时，y___0,这部分图像在第_____象限；对于函数y=-3/x当x<0,y____0，这部分图像在第______象限
>，一，>，二
-
第3题：
在反比例函数y=(k-1)/x的图像的每一条曲线上，y都随x的增大而减少，求k的取值范围
解：因为图像的每一条曲线上，y都随x的增大而减少
所以k-1>0，即k>1
-
第4题：
根据下列条件，分别确定二次函数的解析式：
（1）抛物线y=ax²+bx+c过点（-3，2），（-1，-1），（1，3）；
-
第5题：
11 、点 A （ 2 ， y 1 ） 、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关
系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ） ．
正确答案：<
考点：二次函数图象上点的坐标特征。
分析：本题需先根据已知条件求出二次函数的图象的对称轴，再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系．
解答：解：∵二次函数y=x2﹣2x+1的图象的对称轴是x=1，
在对称轴的右面y随x的增大而增大，
∵点A（2，y1）、B（3，y2）是二次函数y=x2﹣2x+1的图象上两点，
23，
∴y1y2．
故答案为：．
点评：本题主要考查了二次函数图象上点的坐标特征，在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键．
-
第6题：
若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是：
A.f(x,y)的极值点一定是f(x,y)的驻点
B.如果P0是f(x,y)的极值点，则P0点处B2-AC
C.如果P0是可微函数f(x,y)的极值点，则在P0点处df=0
D.f(x,y)的最大值点一定是f(x,y)的极大值点答案：C解析：提示:在题目中只给出f(x,y)在闭区域D上连续这一条件，并未讲函数f(x,y)在P0点是否具有一阶、二阶偏导，而选项A、B判定中均利用了这个未给的条件，因而选项A、B不成立。选项D中f(x,y)的最大值点可以在D的边界曲线上取得，因而不一定是f(x,y)的极大值点，故选项D不成立。
在选项C中，给出p0是可微函数的极值点这个条件，因而f(x,y)在P0偏导存在，且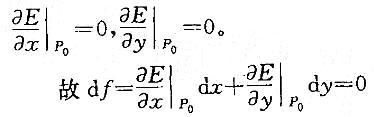
-
第7题：
A.常数k＜-1
B.函数f(x)在定义域范围内，y随着x的增大而减小
C.若点C(-1，m)，点B(2，n)，在函数f(x)的图象上，则m＜n
D.函数f(x)图象对称轴的直线方程是y=x答案：C解析：由图象可知常数k＞0，A项错误；当x＞0时，y随着x的增大而减小，当x＜0时，y随着x的增大而减小，B选项说法不严谨，错误；由反比例函数的公式可得，m=-k＜0，
m＜n，C正确；函数f(x)图象对称轴有两条，y=x和y=-x，D错误。 -
第8题：
如果函数y=kx+b的图像经过A（1,2）和B（0,1），则k=（ ）A.-5
B.1
C.2
D.5答案：B解析： -
第9题：
函数y=cosx在［0，2x］上满足罗尔定理，则ξ= .答案：解析：【答案】π【考情点拨】本题考查了罗尔定理的知识点.
【应试指导】
-
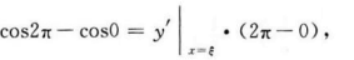
第10题：
若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.
正确答案:错误 -
第11题：
单选题设确定了函数y＝g（x），则（ ）。Ax＝0是函数y＝g（x）的驻点，且是极大值点
Bx＝0是函数y＝g（x）的驻点，且是极小值点
Cx＝0不是函数y＝g（x）的驻点
D存在x＝0的一个小邻域，y＝g（x）是单调的
正确答案： A解析：
g′（x）＝dy/dx＝（dy/dt）·（dt/dx）。dy/dt＝2t/（1＋t2），dx/dt＝1/（1＋t2）。故y′（x）＝2t。又x＝0时，t＝0，g′（x）＝0；t＜0时，x＜0，g′（x）＜0，g（x）单调减少；t＞0时，x＞0，g′（x）＞0，g（x）单调增加。故x＝0是y＝g（x）的驻点，且是极小值点。 -
第12题：
填空题已知集合A＝{a2，a＋1，－3}，B＝{a－3，2a－1，a2＋1}，若A∩B＝{－3}，则实数a的值为____．正确答案： -1解析： ∵A∩B＝{－3}，∴－3∈B
∵ a2＋1＞0
∴集合B中元素有a－3＝－3，或2a－1＝－3．
当a－3＝－3，即a＝0时，A＝{0，1，－3}，B＝{－3，－1，1}，得A∩B＝{1，－3}，与已知A∩B＝{－3}相矛盾，故舍去a＝0；
当2a－1＝－3，即a＝－1时，A＝{1，0，－3}，B＝{－4，－3，2}，A∩B＝{－3}符合题意．
∴a＝－1 -
第13题：
从函数y=f(x)中导出函数x=φ(y),则这两个函数图像在坐标系xOy上是()A、不同的
B、相同的
C、部分相同，部分不同
D、可能相同也可能不同
参考答案：B
-
第14题：
填空： （1） 函数y=10/x的图像在第____象限内，在每一个象限内，y随x的增大而______； （2）函数y=-10/x的图像在第_____象限内，在每一个象限内，y随x的增大而______。
（1）一，三，减少
（2）二，四，增加
-
第15题：
正比例函数ｙ＝ｘ的图像与反比例函数y=k/x图像有一个交点的纵坐标是２，求（１）当ｘ＝－３时，反比例函数ｙ的值；（２）当-3<x<-1时反比例函数ｙ的取值范围？
-
第16题：
下列关于部分函数依赖的叙述中，哪一条是正确的?
A．若X→Y，且存在属性集Z，Z∩Y≠
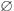，Y→Z，则称Y对X部分函数依赖B．若X→Y，且存在属性集Z，Z∩Y=
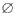，Y→Z，则称Y对X部分函数依赖C．若X→Y，且存在X的真子集X'，
，则称Y对X部分函数依赖D．若K→X，且对于X的任何其子集又X'，都有X'→Y，则称Y对X部分函数依赖
正确答案：C
解析：选项A、B显然是不正确的；按照函数部分依赖的定义，选项C(若X→Y，且存在X的真子集X'，X'→Y，别称Y对X部分数依赖)正确的。而D(若X→Y，且对于X的任何真子集X'，都有，则称Y对X部分函数依赖)是错误的，因为若X→Y，且对于X的任何真子集X'，都有X→Y，则称对Y对X是完全函数依赖。 -
第17题：
若函数y=(a+3)x+a2－9是正比例函数，则a= , 图像过______象限.
正确答案：
3；一，三 -
第18题：
函数y = f (x)在点x = x0,处取得极小值，则必有：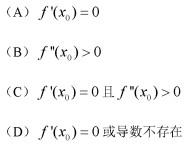
答案：D解析：取得极值，有可能是导数不存在，如函数y = x 在x = 0时取得极小值，但在x = 0处导数不存在。 -
第19题：
若函数f(x)＝log2(5x＋1)，则其反函数y＝f－1(x)的图像过点（ ）A.(2，1)
B.(3，2)
C.(2，3)
D.(4，3)答案：D解析：反函数与原函数的．27与y互换．把x＝3，y＝4代入，f(x)成立。 故反函数过点(4，3)．(答案为D) -
第20题：
若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是（ ）。
A. f(x,y)的极值点一定是f(x,y)的驻点
B.如果P0是f(x,y)的极值点，则P0点处B2-AC)
C.如果P0是可微函数f(x,y)的极值点，则P0点处df=0
D.f(x,y)的最大值点一定是f(x,y)的极大值点答案：C解析：提示：如果P0是可微函数f(x,y)的极值点，由极值存在必要条件，在P0点处有
-
第21题：
已知一次函数的图像过点（3，5）与（-4，-9），则该函数的图像与y轴交点的坐标为（0，-1）。
正确答案:正确 -
第22题：
若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。
- A、f（x，y）的极值点一定是f（x，y）的驻点
- B、如果P0是f（x，y）的极值点，则P0点处B2-AC<0
- C、如果P0是可微函数f（x，y）的极值点，则P0点处df=0
- D、f（x，y）的最大值点一定是f（x，y）的极大值点
正确答案:C -
第23题：
判断题已知一次函数的图像过点（3，5）与（-4，-9），则该函数的图像与y轴交点的坐标为（0，-1）。A对
B错
正确答案： 错解析： 暂无解析