反正切函数y=arctgx的定义域是（）。A、[0，π]B、[-π/2，π/2]C、[-1，1]D、全部实数

题目

反正切函数y=arctgx的定义域是（）。

  • A、[0，π]
  • B、[-π/2，π/2]
  • C、[-1，1]
  • D、全部实数
相似考题

1.设函数f(x)的定义域是(0,1),那么f(x＋1)的定义域是()。A.(0，1)B.(-1，0)C.(1，2)D.(0，2)

2.函数y=arccos(2sinx)的定义域。

3.函数f(x)=x4-24x2+6x在定义域内的凸区间是()A.(-∞，0) B.(-2，2) C.(0，+∞) D.(-∞，+∞)

4.若二次函数y=f（x）的图像过点（0，o），（-1，1）和（-2，o），则f（x）=__________.

参考答案和解析
正确答案:D
更多“反正切函数y=arctgx的定义域是（）。A、[0，π]B、[-π/2，π/2]C、[-1，1]D、全部实数”相关问题

  • 第1题：

    函数f(x)=x4-24x2+6x在定义域内的凸区间是（）

    A.(-，0)
    B.(一2，2)
    C.(0，+)
    D.(-，)

    答案：B
    解析：
    【考情点拨】本题考查了函数的凸区间的知识点．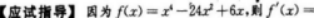

  • 第2题：

    函数f(χ)的定义域为全体实数，且是以5为周期的奇函数( )

    A.1
    B.-1
    C.5
    D.-5

    答案：B
    解析：
    【考情点拨】本题主要考查的知识点为奇函数与周期函数的性质． 【应试指导】∵f(χ)是奇函数，∴f(-2)=-f(2)∴f(2)=-1，

  • 第3题：

    函数y=的定义域是（　　）


    答案：C
    解析：

  • 第4题：

    函数y=的定义域是（　　）

    A.{x｜ z∈R且x≠}
    B.{x｜x≥｝
    C.{x｜x≥2}
    D.{x｜x≥2或x≤1｝

    答案：D
    解析：

  • 第5题：

    过(1，1，-1)，(-2，-2，2)，(1，-1，2)三点的平面方程是( )。

    A.x+3y-2z-6=0
    B.x+3y-2z=0
    C.x-3y-2z-6=0
    D.x-3y-2z=0

    答案：D
    解析：
    设三点依次为A、B、C点，利用三点求两向量，得出所求平面的法向量，再利用平面得点法式方程即可得解

  • 第6题：

    若实值函数f定义域为全体实数，且满足任意x，y:f(x+y)=f(x)f(y)。此时，若f(8)=4，则有f(2)=( )。
    A. 0 D. 2


    答案：C
    解析：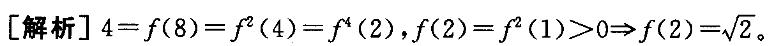

  • 第7题：

    曲线C1：x2+y2-2x=0与曲线C2：y(y-mx-m)=0有4个不同交点，则实数m取值( )。



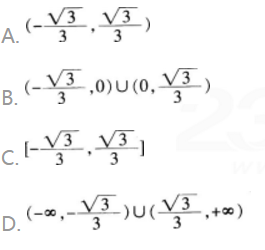    答案：B
    解析：

  • 第8题：

    若二元函数z=arctg（xy），则z（x，y）关于x的偏导数在（1，1）点的值是（）。

    • A、1/2
    • B、1
    • C、2
    • D、0

    正确答案:A

  • 第9题：

    过点（2，-3，1）且平行于向量a=（2，-1，3）和b=（-1，1，-2）的平面方程是（）．

    • A、-x+y+z-4=0
    • B、x-y-z-4=0
    • C、x+y+z=0
    • D、x+y-z+2=0

    正确答案:B

  • 第10题：

    单选题
    若二元函数z=arctg（xy），则z（x，y）关于x的偏导数在（1，1）点的值是（）。
    A

    1/2

    B

    1

    C

    2

    D

    0


    正确答案： B
    解析： 暂无解析

  • 第11题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    －x－y＝0

    B

    x－y－1＝0

    C

    x－y＝0

    D

    x＋y＝0


    正确答案： A
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第12题：

    单选题
    函数的定义域是（　　）．
    A

    （－∞，－1]∪[1，＋∞）

    B

    （－1，1）

    C

    （－∞，－1）∪（1，＋∞）

    D

    [－1，1]


    正确答案： B
    解析：
    对数函数y＝lgx的定义域为{x|x＞0}，所以本题中函数的定义域为{x|x2－1＞0}，即{x|x＞1或x＜－1}．

  • 第13题：

    若实值函数f定义域为全体实数，且满足任意x，y:f(x+y)=f(x)f(y)。此时，若f(8) = 4，则有f(2)=( )。


    答案：C
    解析：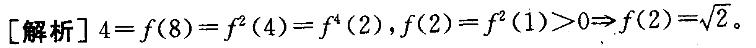

  • 第14题：

    若函数y=f(χ)的定义域是[-1，1)，那么f(2χ-1)的定义域是（ ）

    A.[0，1)
    B.[-3，1)
    C.[-1，1)
    D.[-1，0)

    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为函数的定义域． 【应试指导】由已知，得故求定义域为

  • 第15题：

    下列函数在定义域内，既是奇函数又是增函数的是（）

    A.y=sinx
    B.y=log2x
    C.y=x+8
    D.y=x3

    答案：D
    解析：

  • 第16题：

    曲面z=x2+y2-1在点(1,-1,1)处的切平面方程是( )。

    A.2x-2y-z-3=0
    B.2x-2y+z-5=0
    C.2x+2y-z+1=0
    D.2x+2y+z-1=0

    答案：A
    解析：
    设F(x,y,z)=x2+y2-z-1，则点(1,-1,1)处的切平面法向量为n=(Fx,Fy,Fz)(1,-1,1)={2x,2y,-1)(1,-1,1)={2,-2,-1)，利用平面的点法式方程公式即可得解

  • 第17题：

    点(0，1)是曲线y=ax3+bx+c的拐点，则a、b、c的值分别为:

    A. a=1，b=-3，c=2
    B. a≠0的实数，b为任意实数，c=1
    C. a=1，b=0，c=2
    D.a=0，b 为任意实数，c=1

    答案：B
    解析：
    提示：利用拐点的性质和计算方法计算。如（0，1）是曲线拐点，点在曲线上，代入方程1=c，另外若a=0，曲线：y=bx+c为一条直线，无拐点。所以a≠0。当 a≠0 时，y"=6ax，令y"=0，x=0， 在x=0两侧 y"异号。

  • 第18题：

    过点(2，-3，1)且平行于向量a=(2，-1，3)和b=(-1，1，-2)的平面方程是( ).

    A.-x+y+z-4=0
    B.x-y-z-4=0
    C.x+y+z=0
    D.x+y-z+2=0

    答案：B
    解析：
    A × B =(-1，1，1)，排除 C 、 D ，过点(2，-3，1)=＞ B

  • 第19题：


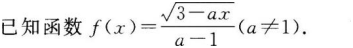
    (1)若a>0，则?(x)的定义域是__________；
    (2)若?(x)在区间(0，1]上是减函数，则实数a的取值范围是__________．


    答案：
    解析：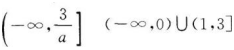


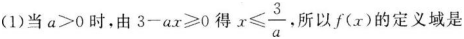
  • 第20题：

    已知实数x，y满足：3(x2+y2+1)=(x-y+1)2，x2013+y2014=（）。

    • A、0
    • B、2
    • C、1
    • D、3

    正确答案:B

  • 第21题：

    问答题
    (X,Y)服从矩形区域D={(x，y)| 0≤X≤2，0≤y≤2}上的均匀分布，则P{0≤X≤1,1≤Y≤2}=_____

    正确答案：
    解析：

  • 第22题：

    单选题
    反正切函数y=arctgx的定义域是（）。
    A

    [0，π]

    B

    [-π/2，π/2]

    C

    [-1，1]

    D

    全部实数


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    x－y＝0

    B

    x＋y＝0

    C

    －x－y＝0

    D

    －x＋y＝0


    正确答案： C
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

相关内容