若（p，q）=1，那么（px-q）就不是一个本原多项式。

题目

相似考题

1.从供选择的答案中选出应填入下列叙述中( )内的正确答案：设关系R和S的元数分别为2和3，那么，RS与(A) 等价。设关系P和Q具有相同的关系模式，所列出的等价式中(B) 是不正确的。设关系模式R(ABC) 上成立的FD集为{A→B) ，pl={AB，BC}为只的一个分解，那么，pl(C) ；若只(ABC) 上成立的 FD集为{A→C，B→C}，p2={AB，AC}为只的一个分解，那么，分解p2(D) ：若R(ABC) 上成立的FD集为{A→B}，p3={AB，BC}为及的一个分解，那么，p3(E)。供选择的答案A：①σ1＞2(RS) ②σ1＞4(RS)③σ1＞2(A×S) ④σ1＞2(A×S)B：①P∩Q=P-(P-Q) ②P∩Q=Q-(Q-P)③P∪Q=P∪(Q-P) ④P∪Q=Q∪(Q-P)C：①不是无损连接分解 ②是无损连接分解③是否无损连接不能确定 ④是否无损连接，由月的具体关系确定D：①保持函数依赖 ②丢失了B→C③丢失了A→C ④是否保持函数依赖，由只的具体关系确定E：①是无损连接，但不保持FD集 ②是无损连接，且保持FD集的分解③是损失连接，且不保持FD集 ④是损失连接，但保持FD集的分解

2.一道数学题为“已知P,Q为两个多项式，请计算2P+Q”，粗心的小明在解题时，将“2P+Q”误看成“P+2Q”，求得的结果为9x2+2x+9，已知Q=x2+3x-2。 (1)求这道数学题的正确答案；(4分) (2)若P=6Q，求x的值。(4分)

3.设p、q是任意命题。P因果蕴涵q指的是：如果p是真的，那么因为p是真的，q也是真的。p反事实蕴涵q指的是：如果p与事实相反，p是真的，那么q也是真的。p严格蕴涵q指的是：必然地，如果p是真的，那么q也是真的。根据上述定义，下列不属于上述三种蕴涵关系的是:A.如果1+1=2，那么0=1 B.如果ab 且 b＜c ，那么ac C.如果甲从台阶上摔断了腿，那么当时他会感觉疼痛 D.如果大气层本就不存在，那么地球上将不会有生命

4.设关系R和s的元数分别为2和3，那么，与(20)等价。设关系 P和Q具有相同的关系模式，所列出的等价式中(21)是不正确的。设关系模式R(ABC)上成立的FD集为{A→B1，p1={AB，B，C)为R的一个分解，那么，p1(22)；若R(ABC)上成立的FD集为{A→C，B→C)，p2={AB，AC}为R的一个分解，那么，分解P2(23)；若R(ABC)上成立的FD集为{B→ C)，p3={AB，BC}为R的一个分解，那么，p3(24)。A．B．C．D．

更多“若（p，q）=1，那么（px-q）就不是一个本原多项式。”相关问题

第1题：

若事件A、B互不相容，且P(A)=p，P(B)=q，则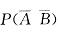等于：

A. 1-p
B. 1-q
C. 1-(p+q)
D.1+p+q

答案：C
解析：
第2题：

下列命题正确的是（）
- A、若p真，q真，则p∨q真
- B、若p真，q假，则p∧q真
- C、若p假，q假，则p→q假
- D、若p假，q假，则p∨q真
正确答案:A
第3题：

系数全为0的多项式，就不是多项式了，是一个实数。

正确答案:错误
第4题：

若p（x）是F（x）中次数大于0的不可约多项式，那么可以得到下列哪些结论？（）
- A、只能有（p（x），f（x））=1
- B、只能有（p（x）
- C、（p（x），f（x））=1或者（p（x）
- D、（p（x），f（x））=1或者（p（x）
正确答案:D
第5题：

每一个次数大于0的本原多项式都可以分解为多少个在Q上不可约的本原多项式的乘积？（）
- A、只有两个
- B、最多四个
- C、无限多个
- D、有限多个
正确答案:D
第6题：

两个本原多项式g（x）和h（x）若在Q[x]中相伴，那么g（x）/h（x）等于多少？（）
- A、±1
- B、任意常数c
- C、任意有理数
- D、任意实数
正确答案:A
第7题：

单选题
若p（x）是F（x）中次数大于0的不可约多项式，那么可以得到下列哪些结论？（）
A
只能有（p（x），f（x））=1
B
只能有（p（x）
C
（p（x），f（x））=1或者（p（x）
D
（p（x），f（x））=1或者（p（x）

正确答案： D
解析：暂无解析
第8题：

判断题
一个次数大于0的本原多项式g（x）在Q上可约，那么g（x）可以分解成两个次数比g（x）次数低的本原多项式的乘积。
A
对
B
错

正确答案：错
解析：暂无解析
第9题：

单选题
f（x）（系数为an…a0）是一个次数n>0的本原多项式，q/p是有理根，那么可以得到f（x）=（px-q）g（x）成立，那么g（x）是什么多项式？（）
A
任意多项式
B
非本原多项式
C
本原多项式
D
无理数多项式

正确答案： D
解析：暂无解析
第10题：

问答题
求出两多项式函数P（x）、Q（x），使得下面等式成立：　　∫[（2x4－1）cosx＋（8x3－x2－1）sinx]dx＝P（x）cosx＋Q（x）sinx＋C

正确答案：
由∫[(2x⁴-1)cosx+(8x³-x²-1)sinx]dx=P(x)cosx+Q(x)sinx+C,两边对x求导,得P′(x)cosx-P(x)sinx+Q′(x)sinx+Q(x)cosx=(2x⁴-1)cosx+(8x³-x²-1)sinx。
等式两边的cosx和sinx项分别相等,则
P′(x)+Q(x)=2x⁴-1①
Q′(x)-P(x)=8x³-x²-1②
将①两边对x求导得P″(x)+Q′(x)=8x³,即
Q′(x)=8x³-P″(x)③
将③代入②整理得
P″(x)+P(x)=x²+1④
假设P(x)=ax²+bx+c,将其代入④得
2a+ax²+bx+c=x²+1
等式两边同次幂的系数应该相等,则a=1,b=0,2a+c=1,解得c=-1。
故P(x)=x²-1,Q(x)=2x⁴-1-P′(x)=2x⁴-1-2x=2x⁴-2x-1。
解析：暂无解析
第11题：

多选题
下列命题不正确的是（）
A
若p真，q真，则p∧q假
B
若p真，q假，则p∨q真
C
若p假，q假，则p→q假
D
若p假，q假，则p∨q真
E
若p假，q真，则p∨q真

正确答案： C,A
解析：暂无解析
第12题：

判断题
若（p，q）=1，那么（px-q）就不是一个本原多项式。
A
对
B
错

正确答案：对
解析：暂无解析
第13题：

下列命题不正确的是（）
- A、若p真，q真，则p∧q假
- B、若p真，q假，则p∨q真
- C、若p假，q假，则p→q假
- D、若p假，q假，则p∨q真
- E、若p假，q真，则p∨q真
正确答案:A,C,D,E
第14题：

两个本原多项式g（x）和f（x），令h（x）=g（x）f（x）记作Cs，若h（x）不是本原多项式，则存在p当满足什么条件时使得p|Cs（s=0，1…）成立？（）
- A、p是奇数
- B、p是偶数
- C、p是合数
- D、p是素数
正确答案:D
第15题：

一个次数大于0的本原多项式g（x）在Q上可约，那么g（x）可以分解成两个次数比g（x）次数低的本原多项式的乘积。

正确答案:正确
第16题：

f（x）（系数为a_n…a₀）是一个次数n>0的本原多项式，q/p是有理根，那么可以得到f（x）=（px-q）g（x）成立，那么g（x）是什么多项式？（）
- A、任意多项式
- B、非本原多项式
- C、本原多项式
- D、无理数多项式
正确答案:C
第17题：

若p/q是f（x）的根，其中（p，q）=1，则f（x）=（px-q）g（x），当x=1时，f（1）/（p-q）是什么？（）
- A、复数
- B、无理数
- C、小数
- D、整数
正确答案:D
第18题：

单选题
每一个次数大于0的本原多项式都可以分解为多少个在Q上不可约的本原多项式的乘积？（）
A
只有两个
B
最多四个
C
无限多个
D
有限多个

正确答案： A
解析：暂无解析
第19题：

单选题
两个本原多项式g（x）和h（x）若在Q[x]中相伴，那么g（x）/h（x）等于多少？（）
A
±1
B
任意常数c
C
任意有理数
D
任意实数

正确答案： C
解析：暂无解析
第20题：

单选题
一个次数大于0的整系数多项式f（x）在Q上可约，那么f（x）可以分解成两个次数比f（x）次数低的什么多项式的乘积。（）
A
整系数多项式
B
本原多项式
C
复数多项式
D
无理数多项式

正确答案： B
解析：暂无解析
第21题：

单选题
若p/q是f（x）的根，其中（p，q）=1，则f（x）=（px-q）g（x），当x=1时，f（1）/（p-q）是什么？（）
A
复数
B
无理数
C
小数
D
整数

正确答案： B
解析：暂无解析
第22题：

单选题
两个本原多项式g（x）和f（x），令h（x）=g（x）f（x）记作Cs，若h（x）不是本原多项式，则存在p当满足什么条件时使得p|Cs（s=0，1…）成立？（）
A
p是奇数
B
p是偶数
C
p是合数
D
p是素数

正确答案： D
解析：暂无解析
第23题：

判断题
系数全为0的多项式，就不是多项式了，是一个实数。
A
对
B
错

正确答案：错
解析：暂无解析

若（p，q）=1，那么（px-q）就不是一个本原多项式。

题目

相似考题

更多“若（p，q）=1，那么（px-q）就不是一个本原多项式。”相关问题

相关内容