单选题通过测量长方形的长L和宽W计算长方形的面积S。已知长方形长和宽的测得值分别为l=10.0cm，w=2.5cm，经评定标准不确定度分别为urel(l)=2%，urel(w)=5%，假设长方形的长L和宽W的测得值彼此独立不相关，计算得到的长方形面积的合成标准不确定度是（）。A 0.24cm2B 0.50cm2C 0.87cm2D 1.35cm2

题目

单选题

通过测量长方形的长L和宽W计算长方形的面积S。已知长方形长和宽的测得值分别为l=10.0cm，w=2.5cm，经评定标准不确定度分别为urel(l)=2%，urel(w)=5%，假设长方形的长L和宽W的测得值彼此独立不相关，计算得到的长方形面积的合成标准不确定度是（）。

0.24cm2

0.50cm2

0.87cm2

1.35cm2

相似考题

1.：一个长方形的长和宽的长度都增加了10%，则新长方形面积比原来的长方形面积增加了（）。A．1%B．20%C．21%D．100%

2.一个长方形的长是宽的2倍，写出这个长方形的面积与宽之间的函数关系式。

3.一个长方形的长减少5cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等。这个长方形的长、宽各是多少

4.求长为20cm，宽为10cm的长方形面积?

参考答案和解析

正确答案： A

解析：

更多“单选题通过测量长方形的长L和宽W计算长方形的面积S。已知长方形长和宽的测得值分别为l=10.0cm，w=2.5cm，经评定标准不确定度分别为urel(l)=2%，urel(w)=5%，假设长方形的长L和宽W的测得值彼此独立不相关，计算得到的长方形面积的合成标准不确定度是（）。A p0.24cmsup2/sup/pB p0.50cmsup2/sup/pC p0.87cmsup2/sup/pD p1.35cmsup2/sup/p”相关问题

第1题：

用长16厘米的铁丝围成各种长方形(长、宽均为整数，且长和宽不相等)，围成最大的一个长方形面积是多少平方厘米?（）
A．16
B．15
C．12
D．9

正确答案：B
设长方形的长为a，宽为b，则这个问题就是求已知a+b=8、且a≠b时，a×b的最大值。为了便于观察，我们分析如下：
8=1+7→1×7=7；8=2+6→2×6=12；
8＝3+5→3×5＝15；8—4+4→4×4＝16；
8＝5+3→5×3＝15；8＝6+2＝6×2＝12；
8＝7+1＝7×1＝7。
我们发现当a从小到大取值，而b从大到小取值时，a与b的积呈现这样一个变化趋势：就是先由小到大，再由大到小，中间是最大的，也就是a与b取的数越接近，它们的乘积就越大。当a—b时，a×b的值最大。由此，得出一条规律：
如果a+b一定，只有当a—b时，a与b的乘积才最大。
由上面的讨论可知，在a十b＝8，且a≠b中，当a＝3，b＝5时，a×b的最大值是：3×5＝15。
所以，所围成的最大的一个长方形面积是l5平方厘米。故本题正确答案为B。
第2题：

：若一个长方形的宽减少了20%，保持长方形的面积不变，长方形的长应增加（）%。
A．45
B．20
C．25
D．30

正确答案：C

长方形的长为a，宽为b，设长方形的长应增加C%，则ab=a(1+C%)b(1-20%)，解得C=25。所以应选择C。
第3题：

用长16厘米的铁丝围成各种长方形（长、宽均为整数，且长和宽不相等），围成的最大的一个长方形的面积是多少平方厘米？（）

A. 16
B. 15
C. 12
D. 9

答案：B
解析：
设长方形的长为a，宽为b，则这个问题就是求已知a+b=8、且a≠b时，axb的最大值。为了便于观察，我们分析如下：
8 = 1 + 7→1X7=7；8 = 2 + 6→2X6 = 12；
8 = 3 + 5→3 X5=15；8 = 4 + 4→4 X 4 = 16；
8 = 5 + 3→5X3=15；8 = 6 + 2 → 6X2 = 12；
8 = 7 + 1→ 7X1=7。
我们发现当a从小到大取值，而b从大到小取值时，a与b的积呈现这样一个变化趋势：就是先由小到大，再由大到小，中间是最大的，也就是a与b取的数越接近，它们的乘积就越大。当a = b时，aXb的值最大。由此，得出一条规律：
如果a+b—定，只有当a =b时，a与b的乘积才最大。
由上面的讨论可知，在a +b=8，且a≠b中，当a=3，b= 5时，aXb的最大值是：3X5 = 15。所以，所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。
第4题：

甲、乙两个长方形的面积相等，甲的长与宽之比是5：4，乙的长与宽之比是6：5，甲、乙两个长方形的周长比是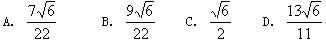

答案：B
解析：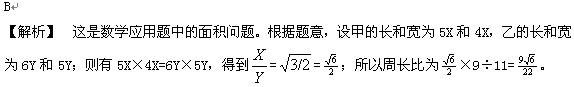
第5题：

如下图，大长方形被分为四个较小长方形，已知四个长方形的面积已标示出来，且这个大长方形的长和宽均为整数，那么图中双向箭头之间的部分是多长？（）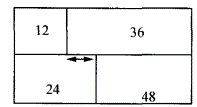

A. 1
B. 2
C. 1 或 2
D. 3

答案：C
解析：
第6题：

某长方形长和宽的比是4:3，如果长减少4米，宽增加6米则变成一个正方形，原长方形的面积为（__）平方米？

A. 900
B. 1200
C. 1500
D. 1800

答案：B
解析：
本题考查基础几何问题。设长为4x，宽为3x，4x-4=3x+6，解得x=10，则长方形长40，宽30，面积为30*40=1200
第7题：

九个边长分别为1，4，7，8，9，10，14，15，18的正方形可以拼成一个长方形，问这个长方形的长和宽是（）。

正确答案:33和32
第8题：

单选题
一个长方形长、宽分别为a、b。该长方形的面积为（）。
A
a+b
B
a﹣b
C
a/b
D
ab

正确答案： B
解析：暂无解析
第9题：

单选题
通过测量长方形的长L和宽W计算长方形的面积S。已知长方形长和宽的测得值分别为l=10.0cm，w=2.5cm，经评定标准不确定度分别为urel(l)=2%，urel(w)=5%，假设长方形的长L和宽W的测得值彼此独立不相关，计算得到的长方形面积的合成标准不确定度是（）。
A
0.24cm2
B
0.50cm2
C
0.87cm2
D
1.35cm2

正确答案： C
解析：
第10题：

给长方形的长增加2，宽增加5恰好可以得到一个面积为100的正方形，则原长方形的周长( )。
A．13
B．26
C．40
B D．46

正确答案：B
第11题：

一个长方形的长与宽的比是14：5，如果长减少l3厘米，宽增加l3厘米，则面积增加182平方厘米，那么原长方形面积是多少平方厘米?

A.448
B.630
C.812
D.1120

答案：B
解析：
设原长方形的长为l4a，宽为5a，由题意可得，(14a一l3)x(5a+13)=14a×5a+182，解得a=3，
原长方形面积是14×3×5×3=630平方厘米，应选择8。
第12题：

如右图甲、乙两个长方形的面积相等，甲的长与宽之比是5：4，乙的长与宽之比是6：5，甲、乙两个长方形的周长比是（）。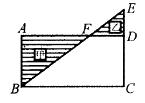

答案：B
解析：
方法一：
因为甲的长与宽之比是5 : 4，所以我们设甲的长与宽分别是5x、4x，则甲的面积为20X2，周长为18x；乙的长与宽之比是6 : 5，所以我们设乙的长与宽分别是6y，5y。则乙的面积为30y2，周长为22y；因
第13题：

若将一个长方形的长缩短1厘米，宽加长8厘米，所得新长方形的周长和面积分别是原长方形的2倍和4倍，则原长方形的长是：

A.4厘米
B.5厘米
C.6厘米
D.7厘米

答案：B
解析：
第14题：

给长方形的长增加2，宽增加5恰好可以得到一个面积为100的正方形，则原长方形的周长( )。

A. 13
B. 26
C. 40
D. 46

答案：B
解析：
故答案为B。
第15题：

X1与X2不相关，对应的标准不确定度分别为w (x1)和W (x2).则，X1-X2的合成标准不确定度为（）。

答案：D
解析：
。
第16题：

一个长方形长、宽分别为a、b。该长方形的面积为（）。
- A、a+b
- B、a﹣b
- C、a/b
- D、ab
正确答案:D
第17题：

单选题
测量某矩形周长时，用两个不同仪器分别量长和宽，宽度测量值L1= 10. 00cm,长度测得值L2= 20. 00cm，L1和L2的相对标准不确定度分别为urel(L1)=2.0%，urel(L2)= 1.2%,该矩形周长测得值的合成标准不确定度是（）。
A
0.31cm
B
0.62cm
C
1. 4cm
D
2.8cm

正确答案： C
解析：

题目

相似考题

参考答案和解析

相关内容