单选题假设一个回避风险的投资者。投资组合1的期望收益率是14%，标准差σ=0.18；投资组合2的标准差σ=0.25，年末现金流为5000和14000美元的概率是相等的，若在投资组合1和投资组合2的选择上没有差别，则投资组合2的价格是（　　）。A 7712.14 B 7734.78C 7756.43 D 7825.13 E 7953.45

题目
单选题
假设一个回避风险的投资者。投资组合1的期望收益率是14%，标准差σ=0.18；投资组合2的标准差σ=0.25，年末现金流为5000和14000美元的概率是相等的，若在投资组合1和投资组合2的选择上没有差别，则投资组合2的价格是（　　）。
A

7712.14  

B

7734.78

C

7756.43  

D

7825.13  

E

7953.45

相似考题

1.以下哪些是资产组合理论的假定()。A、投资者仅以期望收益率和方差来评价资产组合B、投资者是不知足的和风险厌恶的C、投资者选择期望收益率最高的投资组合D、投资者选择风险最小的组合

2.已知债券1 的收益率为10%，标准差为3%， 债券2 的收益率为15%，标准差为5%，债券1和债券2的收益不相关，现将债券1 与债券2组成一个投资组合，如果组合的标准差为4.6%，那么组合的期望收益为：（ ）A．10%B．14%C．16%D．8%

3.若无风险收益率为4.8%,你的客户的投资组合的标准差为11%,该投资组合的期望收益率为9%,那么该投资组合的夏普指标为( )A．0.25B．0.45C．0.20D．0.38

4.投资组合理论的基本假设是（ ）。A．投资者仅以期望收益率和方差(或标准差)评价单个证券和证券组合B．投资者是不知足的和厌恶风险的C．投资者总是希望持有有效资产组合D．投资者的投资为多个投资期

更多“单选题假设一个回避风险的投资者。投资组合1的期望收益率是14%，标准差σ=0.18；投资组合2的标准差σ=0.25，年末现金流为5000和14000美元的概率是相等的，若在投资组合1和投资组合2的选择上没有差别，则投资组合2的价格是（　　）。A 7712.14 B 7734.78C 7756.43 D 7825.13 E 7953.45”相关问题

  • 第1题：

    假定投资者的效用函数为 U=E （r）-0.005Ao*2 ，给定以下投资组合： 投资组合 预期收益 % 标准差 % 1 12 30 2 15 50 3 21 16 4 24 21 如果投资者的风险厌恶系数 A=4 ，投资者会选择哪种投资？

    A.1
    B.2
    C.3
    D.4

    答案：D
    解析：

    由于投资组台4的效用最大,因此应当选择投资组合4

  • 第2题：

    期望收益率为12%的充分分散投资组合，无风险利率是4%，市场组合收益率是8%，标 准差是0.2,若是有效组合，则投资组合收益率标准差是（ ）

    A.0.2
    B.0.3
    C.0.4
    D.0.6
    E.0.8

    答案：C
    解析：
    充分分散化的投资组合，其标准差应该是只包含系统性风险。又根据SML可以 计算出该组合的收益率标准差、

  • 第3题：

    资产组合M的期望收益率为18%，标准差为27.9%，资产组合N的期望收益率为13%，标准差率为1.2，投资者张某和赵某决定将其个人资产投资于资产组合M和N中，张某期望的最低收益率为16%，赵某投资于资产组合M和N的资金比例分别为30%和70%。
    要求：
    （1）计算资产组合M的标准差率；
    （2）判断资产组合M和N哪个风险更大？
    （3）为实现期望的收益率，张某应在资产组合M上投资的最低比例是多少？
    （4）判断投资者张某和赵某谁更厌恶风险，并说明理由。（2017年）


    答案：
    解析：
    （1）资产组合M的标准差率=27.9%/18%=1.55。
    （2）资产组合N的标准差率为1.2，小于资产组合M的标准差率1.55，故资产组合M的风险更大。
    （3）设张某应在资产组合M上投资的最低比例是X，则：18%X+13%×（1-X）=16%，求得：X=60%，为实现期望的收益率，张某应在资产组合M上投资的最低比例是60%。
    （4）张某在资产组合M（高风险）上投资的最低比例是60%，而在资产组合N（低风险）上投资的最高比例是40%；而赵某投资于资产组合M（高风险）和N（低风险）的资金比例分别为30%和70%。由于赵某投资于资产组合M（高风险）的比例低于张某投资于资产组合M（高风险）的比例，所以赵某更厌恶风险。

  • 第4题：

    某企业拟进行股票投资，现有甲、乙两只股票可供选择，具体资料如下：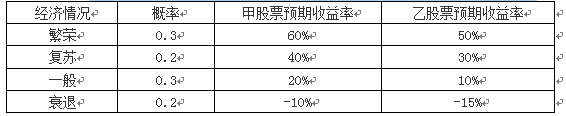

    已知甲、乙股票收益率的标准差分别为25.30%和23.75%。
    要求：
    （1）分别计算甲、乙股票收益率的期望值和标准差率，并比较其风险大小；
    （2）假设投资者将全部资金按照60%和40%的比例分别投资购买甲、乙股票构成投资组合，已知甲、乙股票的β系数分别为1.4和1.8，市场组合的收益率为10%，无风险收益率为4%，请计算投资组合的β系数和组合的风险收益率；
    （3）根据资本资产定价模型计算组合的必要收益率。


    答案：
    解析：
    （1）甲股票收益率的期望值=0.3×60%+0.2×40%+0.3×20%+0.2×（-10%）=30%
    乙股票收益率的期望值=0.3×50%+0.2×30%+0.3×10%+0.2×（-15%）=21%
    甲股票收益率的标准差率=25.30%/30%=0.84
    乙股票收益率的标准差率=23.75%/21%=1.13
    由于甲、乙股票收益率的期望值不同，因此不能根据其收益率的标准差来比较风险，而应根据收益率的标准差率来比较风险。乙股票收益率的标准差率大于甲股票收益率的标准差率，所以，乙股票的风险大于甲股票的风险。
    （2）投资组合的β系数和组合的风险收益率：
    组合的β系数=60%×1.4+40%×1.8=1.56
    组合的风险收益率=1.56×（10%-4%）=9.36%。
    （3）组合的必要收益率=4%+9.36%=13.36%。

  • 第5题：

    某投资者选择证券甲和证券乙进行组合投资，选两种证券的分析数据如下①证券甲的收益率期型值利和标准差分别为0.08和10%;②证券乙的收益率期望值和标准差分别为为0.16 和 14%，③证券甲和证券乙的相关系数为1，④证券甲和证券乙的投资比重分别为0.45利0.55。那么，( )。

    A: 该投瓷者的投资组合的期型收盏率等于 0.124
    B: 该投资者的投资组合的标准差等于 14 2%
    C: 该投资者的投资组合的期型收益率等于0.14
    D: 该投资者的投资组合的标准差等于12.2%

    答案：A,D
    解析：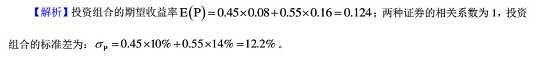

  • 第6题：

    资产组合M的期望收益率为18％，标准差为27．9％，资产组合N的期望收益率为13％，标准差率为1．2，投资者张某和赵某决定将其个人资产投资于资产组合M和N中，张某期望的最低收益率为16％，赵某投资于资产组合M和N的资金比例分别为30％和70％。 计算资产组合M的标准差率。


    正确答案: 资产组合M的标准差率=27．9％／18％=1.55

  • 第7题：

    资产组合M的期望收益率为18％，标准差为27．9％，资产组合N的期望收益率为13％，标准差率为1．2，投资者张某和赵某决定将其个人资产投资于资产组合M和N中，张某期望的最低收益率为16％，赵某投资于资产组合M和N的资金比例分别为30％和70％。 判断投资者张某和赵某谁更厌恶风险，并说明理由。


    正确答案: 张某在资产组合M(高风险)上投资的最低比例是60％，在资产组合N(低风险)上投资的最高比例是40％，而赵某投资于资产组合M和N的资金比例分别为30％和70％；因为资产组合M的风险大于资产组合N的风险，并且赵某投资于资产组合M(高风险)的比例低于张某投资于资产组合M(高风险)的比例，所以赵某更厌恶风险。

  • 第8题：

    下列有关两项资产构成的投资组合的表述中，正确的是（）。

    • A、如果相关系数为+1，则投资组合的标准差等于两项资产标准差的算术平均数
    • B、如果相关系数为-1，则投资组合的标准差最小，甚至可能等于0
    • C、如果相关系数为0，则投资组合不能分散风险
    • D、如果相关系数为-1，则投资组合不能分散风险

    正确答案:B

  • 第9题：

    马柯威茨的“风险厌恶假设”是指（）。

    • A、投资者都依据期望收益率评价证券组合的收益水平、依据方差评价证券组合的风险水平，并采用投资组合理论选择最优证券组合
    • B、如果两种证券组合具有相同的期望收益率和不同的收益率方差，那么投资者选择方差较小的组合
    • C、投资者对证券的收益、风险及证券间的关联性具有完全相同的预期
    • D、如果两种证券组合具有相同的收益率方差和不同的期望收益率，那么投资者选择期望收益率高的组合

    正确答案:B

  • 第10题：

    多选题
    资产组合理论的基本假设包括（）。
    A

    均方准则：投资者仅仅以期望收益率和方差（标准差）来评价资产组合

    B

    投资者理性：投资者是不知足的和风险厌恶的

    C

    瞬时投资：投资者的投资为单一投资期，多期投资是单期投资的不断重复

    D

    有效组合：在资金约束下，投资者希望持有具有最高收益的均方标准的组合


    正确答案： B,A
    解析： 暂无解析

  • 第11题：

    单选题
    股票A的期望收益率是14%，标准差为25%，无风险利率是4%。一个投资者的效用函数： U=E（r）-0.005Aσ2。若该投资者在投资风险组合和无风险资产之间是没有差异的，则A=（　　）。
    A

    310  

    B

    320

    C

    350  

    D

    380  

    E

    390


    正确答案： A
    解析：
    对两个投资无差异，则两个投资的效用必然相同。由于国库券是无风险的，它的效用是4%的收益率，通过效用函数0.04=0.14-0.005A×0.252，解得A=320。

  • 第12题：

    单选题
    现有一投资组合，投资组合的贝塔值为2，投资组合的收益与市场协方差为8，市场收益率标准差为 （）。
    A

    2

    B

    4

    C

    6

    D

    1


    正确答案： B
    解析：

  • 第13题：

    某投资者选择证券甲和证券乙进行组合投资，这两种证券的分析数据如下：①证券甲的收益率期望值和标准差分别为0.08和10%；②证券乙的收益率期望值和标准差分别为0.16和14%；③证券甲和证券乙的相关系数为1；④证券甲和证券乙的投资比重分别为0.45和0.55。那么，()。

    A.该投资者的投资组合的期望收益率等于0.124
    B.该投资者的投资组合的标准差等于14.2%
    C.该投资者的投资组合的期望收益率等于0.14
    D.该投资者的投资组合的标准差等于12.2%

    答案：A,D
    解析：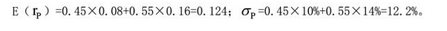

  • 第14题：

    现有一投资组合，投资组合的贝塔值为2，投资组合的收益与市场协方差为8，市场收益率标准差为（ ）。

    A.2
    B.4
    C.6
    D.1

    答案：A
    解析：
    根据贝塔系数的计算式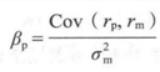，，其中βp表示贝塔系数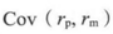，表示投资组合p的收益与市场收益的协方差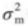；是市场收益的方差。所以市场收益的方差=8/2=4，标准差的平方=方差，标准差=。
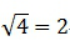    考点
    风险指标

  • 第15题：

    资产组合M的期望收益率为18%，标准差为27.9%，资产组合N的期望收益率为13%，标准差率为1.2，投资者张某和赵某决定将其个人资产投资于资产组合M和N中，张某期望的最低收益率为16%，赵某投资于资产组合M和N的资金比例分别为30%和70%。
    要求：
    （1）计算资产组合M的标准差率；
    （2）判断资产组合M和N哪个风险更大？
    （3）为实现期望的收益率，张某应在资产组合M上投资的最低比例是多少？
    （4）判断投资者张某和赵某谁更厌恶风险，并说明理由。


    答案：
    解析：
    （1）资产组合M的标准差率=27.9%/18%=1.55。
    （2）资产组合N的标准差率为1.2小于资产组合M的标准差率1.55，故资产组合M的风险更大。
    （3）设张某应在资产组合M上投资的最低比例是X，则：18%X+13%×（1-X）=16%，求得：X=60%，为实现期望的收益率，张某应在资产组合M上投资的最低比例是60%。
    （4）张某在资产组合M（高风险）上投资的最低比例是60%，而在资产组合N（低风险）上投资的最高比例是40%；而赵某投资于资产组合M（高风险）和N（低风险）的资金比例分别为30%和70%。由于赵某投资于资产组合M（高风险）的比例低于张某投资于资产组合M（高风险）的比例，因此赵某更厌恶风险。

  • 第16题：

    （2017年）资产组合M的期望收益率为18%，标准差为27.9%；资产组合N的期望收益率为13%，标准差率为1.2。投资者张某决定将其个人资金投资于资产组合M和N中，张某期望的最低收益率为16%。
    　　要求：
    　　（1）计算资产组合M的标准差率。
    　　（2）判断资产组合M和N哪个风险更大。
    　　（3）为实现其期望的收益率，张某应在资产组合M上投资的最低比例是多少？


    答案：
    解析：
    （1）资产组合M的标准差率＝27.9%÷18%＝1.55
    　　（2）资产组合M的标准差率1.55大于资产组合N的标准差率1.2，说明资产组合M的风险更大。
    　　（3）假设投资资产组合M的比例为W，依据资料，有：W×18%＋（1－W）×13%＝16%
    　　解得：W＝60%，即张某应在资产组合M上投资的最低比例是60%。

  • 第17题：

    资产组合M的期望收益率为18％，标准差为27．9％，资产组合N的期望收益率为13％，标准差率为1．2，投资者张某和赵某决定将其个人资产投资于资产组合M和N中，张某期望的最低收益率为16％，赵某投资于资产组合M和N的资金比例分别为30％和70％。 判断资产组合M和N哪个风险更大？


    正确答案: 资产组合N的标准差率为1．2小于资产组合M的标准差率1．55，故资产组合M的风险更大。

  • 第18题：

    贝塔系数和标准差都能衡量投资组合的风险。下列关于投资组合的贝塔系数和标准差的表述中，正确的有（）。

    • A、贝塔系数度量的是投资组合的系统风险
    • B、标准差度量的是投资组合的非系统风险
    • C、投资组合的贝塔系数等于被组合各证券贝塔系数的算术加权平均值
    • D、投资组合的标准差等于被组合各证券标准差的算术加权平均值

    正确答案:A,C

  • 第19题：

    资产组合M的期望收益率为18％，标准差为27．9％，资产组合N的期望收益率为13％，标准差率为1．2，投资者张某和赵某决定将其个人资产投资于资产组合M和N中，张某期望的最低收益率为16％，赵某投资于资产组合M和N的资金比例分别为30％和70％。 为实现期望的收益率，张某应在资产组合M上投资的最低比例是多少？


    正确答案: 设张某应在资产组合M上投资的最低比例是×：18％××+13％×（1-×）=16％，解得：×=60％。
    为实现期望的收益率，张某应在资产组合M上投资的最低比例是60％。

  • 第20题：

    王先生打算投资一风险资产组合，年末来自该资产组合的现金流可能为70000或200000元，概率相等，均为0．5；可供选择的无风险国库券投资年利率为6％。假定王先生可以以上题中的价格购买该资产组合，该投资的期望收益率为（）

    • A、12％
    • B、13％
    • C、14％
    • D、15％

    正确答案:C

  • 第21题：

    多选题
    贝塔系数和标准差都能衡量投资组合的风险。下列关于投资组合的贝塔系数和标准差的表述中，正确的有（  ）。
    A

    标准差度量的是投资组合的非系统风险

    B

    投资组合的贝塔系数等于被投资组合各证券贝塔系数的算术加权平均值

    C

    投资组合的标准差等于被投资组合各证券标准差的算术加权平均值

    D

    贝塔系数度量的是投资组合的系统风险


    正确答案： C,D
    解析：

  • 第22题：

    单选题
    某资产组合，年末来自该资产组合的现金流可能为70000美元或200000美元，概率相等，均为0.5；无风险国库券投资年利率为6％，如果投资者要求8％的风险溢价，则投资者愿意为购买该资产组合支付的价格为（　　）美元。
    A

    118421  

    B

    135000  

    C

    125015  

    D

    123150  

    E

    115612


    正确答案： C
    解析：
    资产组合的预期现金流为：0.5×70000+0.5×200000=135000美元；
    投资者要求的回报率为：8%+6%=14%；
    资产组合的现值为：135000/（1+14%）=118421美元。

  • 第23题：

    单选题
    一个投资组合的预期收益率是14％，标准差是25％，无风险利率是4％。一个投资者的效用函数是：U=E（r）-0.5Aσ2。若投资者对风险投资组合和无风险资产感到无差异，则A=（　　）。
    A

    3.1

    B

    3.2  

    C

    3.5  

    D

    3.8  

    E

    3.9


    正确答案： E
    解析：
    如果无差异，则两种投资的效用就应该一样。对于无风险资产，标准差是零，资产的效用就是预期收益，即U=0.04。因此有风险的投资效用也是0.04。通过效用函数0.04=0.14-0.5A×0.252，解得A=3.2。

相关内容