单选题计算弯矩系数αM=0.450，计算轴力系数ηN=1.450，则托梁跨中截面的弯矩Mb和轴心拉力Nb与下列（　　）组数据最为接近。A 347.7kN·m；238.6kNB 354.27kN·m；239.7kNC 365kN·m；245.6kND 372.35kN·m；318.92kN

题目
单选题
计算弯矩系数αM=0.450，计算轴力系数ηN=1.450，则托梁跨中截面的弯矩Mb和轴心拉力Nb与下列（　　）组数据最为接近。
A

347.7kN·m；238.6kN

B

354.27kN·m；239.7kN

C

365kN·m；245.6kN

D

372.35kN·m；318.92kN

相似考题

1.某单跨简支梁，计算跨度l0=6m，永久荷载标准值gk=16kN/m(含自重)，可变荷载标准值qk=7kN/m(可变荷载的组合值系数是0.7)，则基本组合时梁跨中最大弯矩设计值为()。A、103.5kN.mB、128.07kN.mC、130.5kN.mD、141.3kN.m

2.承重墙梁，各部分尺寸见图及表，托梁混凝土强度等级为C20，纵向受力钢筋采用HRB335，砖强度为MU10，水泥砂浆强度等级采用M5，荷载设计值Q1=23.8kN/m，Q2=116kN/m。2.计算弯矩系数αM与计算轴力系数ηN与下列（　　）组数据最为接近。A. αM=0.406；ηN=1.430B. αM=0.432；ηN=1.430C. αM=0.450；ηN=1.250D. αM=0.485；ηN=1.336

3.计算地下室顶面的地震弯矩设计值M（kN·m），与下列何项数值最为接近？（　　）A、182391 B、237108 C、232090 D、218869

4.某一级公路上的一座预应力混凝土梁桥，其结构安全等级为一级。经计算知：该梁的跨中截面弯矩标准值为：梁自重弯矩2500kN·m；汽车作用弯矩（含冲击力）1800kN·m；人群作用弯矩200kN·m。试问，该梁跨中作用效应基本组合的弯矩设计值（kN·m），与下列何项数值最接近？（　　）A. 6400B. 6300C. 5800D. 5700

更多“单选题计算弯矩系数αM=0.450，计算轴力系数ηN=1.450，则托梁跨中截面的弯矩Mb和轴心拉力Nb与下列（　　）组数据最为接近。A 347.7kN·m；238.6kNB 354.27kN·m；239.7kNC 365kN·m；245.6kND 372.35kN·m；318.92kN”相关问题

  • 第1题：

    承重墙梁，各部分尺寸见图及表，托梁混凝土强度等级为C20，纵向受力钢筋采用HRB335，砖强度为MU10，水泥砂浆强度等级采用M5，荷载设计值Q1=23.8kN/m，Q2=116kN/m。




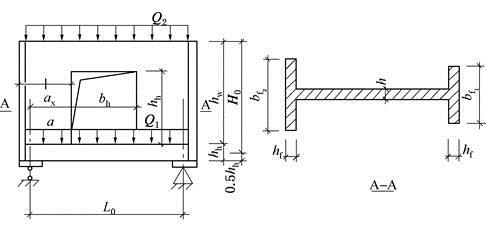
    3.计算弯矩系数αM=0.450，计算轴力系数ηN=1.450，则托梁跨中截面的弯矩Mb和轴心拉力Nb与下列（　　）组数据最为接近。

    A. 347.7kN·m；238.6kN
    B. 354.27kN·m；239.7kN
    C. 365kN·m；245.6kN
    D. 372.35kN·m；318.92kN

    答案：A
    解析：
    M1=Q1l02/8=23.8×6.052/8=108.89kN·m；
    M2=Q2l02/8=116×6.052/8＝530.74kN·m；
    根据《砌体结构设计规范》（GB 50003—2011）第7.3.6条式（7.3.6-1）计算，托梁跨中截面的弯矩为：Mb=M1+αMM2=108.89+0.450×530.74＝347.7kN·m；
    根据第7.3.6条式（7.3.6-2）计算，轴心拉力为：Nb=ηNM2/H0=1.45×530.74/3.225=238.6kN。由此可知，A项数值最为接近。

  • 第2题：


    试问，托梁跨中最大弯矩Mb (kN * m)，与下列何项数值最为接近？
    (A) 106 (B) 174 (C) 191 (D)370


    答案：C
    解析：

  • 第3题：

    对某钢筋混凝土简支T梁桥进行承载能力评定，该桥计算跨径为20.0m，桥面横向布置为0.3m（栏杆）+9.0m（车行道）+0.3m（栏杆）=9.6m，无人行道，设计荷载等级为公路-Ⅱ级。根据前期检测结果得到的跨中截面正弯矩计算结果和各分项检算系数见下表。（3）根据表中数据，跨中截面正弯矩实际抗力效应R的计算结果应为（ ）。

    A：4848.6kN.m
    B：5103.8kN.m
    C：4329.2kN.m
    D：843.0kN.m

    答案：C
    解析：
    实际抗力效应R=4900×0.93×（1-0.05）=4329.2（kN.m）

  • 第4题：

    某后张法预应力混凝土简支T梁,标准跨径25m,计算跨径24.6m,设计跨中弯矩M=3200kN·m,跨中理论计算挠度25.0mm。为检验其承载能力，实施单梁静载试验。静载试验采用砂袋沿梁宽和长度范围均布加载,荷载挠度为44.3kN/m。最大试验荷载下实测跨中挠度22.5mm,残余挠度2.65mm。（资料:该梁汽车荷载下的冲击系数μ=0.268,均布荷载作用下跨中弯矩计算公式M=ql2/8）1、该梁试验跨中弯矩值为（ ）kN·m。

    A.3351
    B.3461
    C.272
    D.277

    答案：A
    解析：
    44.3×24.6×24.6÷8=3351kN·m

  • 第5题：

    某后张法预应力混凝土简支T梁,标准跨径25m,计算跨径24.6m,设计跨中弯矩M=3200kN·m,跨中理论计算挠度25.0mm。为检验其承载能力，实施单梁静载试验。静载试验采用砂袋沿梁宽和长度范围均布加载,荷载挠度为44.3kN/m。最大试验荷载下实测跨中挠度22.5mm,残余挠度2.65mm。（资料:该梁汽车荷载下的冲击系数μ=0.268,均布荷载作用下跨中弯矩计算公式M=ql2/8）1、该梁试验跨中弯矩值为（ ）kN·m。（2018检师真题）

    A.3351
    B.3461
    C.272
    D.277

    答案：A
    解析：
    44.3×24.6×24.6÷8=3351kN·m

  • 第6题：

    某7片主梁预应力混凝土T梁桥，主梁布置如图所示。设计荷载为公路—Ⅰ级。

    假设该桥的计算跨径为29.16m，设计荷载为公路—Ⅰ级荷载，汽车冲击系数μ＝0.212。则2号梁的跨中截面最大弯矩最接近于（　　）kN·m。

    A.4900
    B.3675
    C.2379
    D.1840

    答案：C
    解析：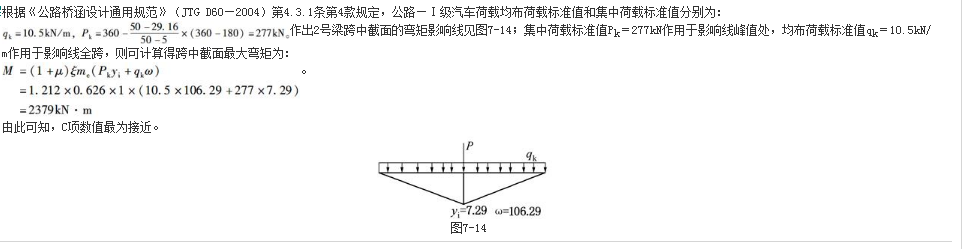

  • 第7题：

    某5片主梁混凝土简支T梁桥，其计算跨径为L＝14.5m，设计荷载为公路—Ⅰ级。已求得单片主梁跨中弯矩汽车荷载横向分布系数为0.412，汽车荷载冲击系数为0.125，试计算单片主梁跨中汽车荷载引起的弯矩值最接近于（　　）kN·m。

    A.364
    B.390
    C.494
    D.994

    答案：C
    解析：

  • 第8题：

    若按弹性理论计算的弯矩Me＝100kN·m，取弯矩调幅系数β为0.2，则调幅后的弯矩Ma为：（）。

    • A、20kN·m
    • B、80kN·m
    • C、83.3kN·m
    • D、120kN·m

    正确答案:B

  • 第9题：

    当主梁抗扭能力小（行车道板厚h1与主梁高h之比大于1／4）时，多跨连续单向板跨中弯矩计算公式为M中＝（）；支点弯矩计算公式为M支＝（）。其中M0是与之跨径相同的简支板跨中弯矩值。


    正确答案:0.7M0；-0.7M0

  • 第10题：

    填空题
    当主梁抗扭能力小（行车道板厚h1与主梁高h之比大于1／4）时，多跨连续单向板跨中弯矩计算公式为M中＝（）；支点弯矩计算公式为M支＝（）。其中M0是与之跨径相同的简支板跨中弯矩值。

    正确答案： 0.7M0,-0.7M0
    解析： 暂无解析

  • 第11题：

    单选题
    若已知梁的短期效应刚度Bs＝29732.14kN·m2，按荷载效应的标准组合计算的跨中弯矩值Mk＝90kN·m，按荷载效应的准永久组合计算的跨中弯矩值Mq＝50kN·m，梁受压区配有218的钢筋，则跨中挠度最接近于（　　）mm。
    A

    10.2

    B

    14.3

    C

    16.3

    D

    17.9


    正确答案： C
    解析：
    根据《混凝土结构设计规范》（GB 50010—2010）（2015年版）第7.2.5条第1款规定，钢筋混凝土受压构件的配筋率为：ρ′＝As′/（bh0）；纵向受拉钢筋配筋率为：ρ＝As/（bh0）。
    则荷载长期效应组合对挠度增大的影响系数为：θ＝2.0－0.4×ρ′/ρ＝2.0－0.4×509/942＝1.78。
    根据第7.2.2条式（7.2.2-1）规定，受弯构件的长期刚度为：
    B＝MkBs/[Mq（θ－1）＋Mk]＝90×29732.14/[50×（1.78－1）＋90]＝20743.35kN·m2。
    跨中挠度为：f＝5×Mkl02/（48B）＝5×90×62/（48×20743.35）＝16.27mm。
    选项中与结果最接近的是16.3，因此答案选C项。

  • 第12题：

    单选题
    计算弯矩系数αM与计算轴力系数ηN与下列（　　）组数据最为接近。
    A

    αM=0.406；ηN=1.430

    B

    αM=0.432；ηN=1.430

    C

    αM=0.450；ηN=1.250

    D

    αM=0.485；ηN=1.336


    正确答案： C
    解析：
    根据《砌体结构设计规范》（GB 50003—2011）第7.3.6条进行计算，由图4-23可知，设墙梁为简支墙梁，则：
    ①计算弯矩系数αM
    Hb/l0=0.75/6.05=0.124＜16＝0.166，取hb/l0＝0.124；
    洞口对托梁弯矩的影响系数为：ψM＝4.5-10a/l0=4.5-10×1.275/6.05＝2.39；
    则弯矩系数为：αM＝ψM（1.7hb/l0-0.03）＝2.39×（1.7×0.124-0.03）=0.432。
    ②计算轴力系数ηN
    hw/l0=2.85/6.05=0.471＜1，取hw/l0=0.471；
    ηN=0.44+2.1hw/l0=0.44+2.1×0.471=1.43。由此可知，B项数值最为接近。

  • 第13题：

    某三层商住楼，底层局部采用两跨连续墙梁结构。局部平面图及剖面如图4-8所示。开间为3.3m，底层层高3.9m，其余两层为3.0m，墙厚为190mm。托梁下均设有壁柱 (每边凸出墙面200mm×590mm)。墙体采用MU10混凝土砌块和Mb10混合浆砌筑(f=2.79MPa)。楼盖及屋盖采用钢筋混凝土现浇板，厚120mm。托梁混凝土采用C30(fc=14.3N/mm2)，纵向钢筋为HRB400(fv=360N/mm2)，箍筋采用HPB235(f=210N/mm2)。屋面恒荷载标准值为4.8kN/m2，屋面活荷载标准值为0.5kN/m2，楼面恒荷载标准值为3.8kN/m2，活荷载标准值为2.0kN/m2，墙体自重标准值(包括双面粉刷)为2.61kN/m2，梁支座下设190mm×190mm上下贯通钢筋混凝土构造柱。托梁的截面尺寸bb×hb=250mm×600mm(石灰水粉刷)。各层墙顶均设截面为190mm×190mm的钢筋混凝土圈梁。



    计算弯矩系数αM与计算轴力系数ηN与下列( )组数据最为接近。

    A.. αM=0.406；ηN=1.430
    B.. αM=0.432；ηN=1.430
    C.. αM=0.450；ηN=1.250
    D.. αM=0.485；ηN=1.336

    答案：B
    解析：

  • 第14题：

    某三层商住楼，底层局部采用两跨连续墙梁结构。局部平面图及剖面如图4-8所示。开间为3.3m，底层层高3.9m，其余两层为3.0m，墙厚为190mm。托梁下均设有壁柱 (每边凸出墙面200mm×590mm)。墙体采用MU10混凝土砌块和Mb10混合浆砌筑(f=2.79MPa)。楼盖及屋盖采用钢筋混凝土现浇板，厚120mm。托梁混凝土采用C30(fc=14.3N/mm2)，纵向钢筋为HRB400(fv=360N/mm2)，箍筋采用HPB235(f=210N/mm2)。屋面恒荷载标准值为4.8kN/m2，屋面活荷载标准值为0.5kN/m2，楼面恒荷载标准值为3.8kN/m2，活荷载标准值为2.0kN/m2，墙体自重标准值(包括双面粉刷)为2.61kN/m2，梁支座下设190mm×190mm上下贯通钢筋混凝土构造柱。托梁的截面尺寸bb×hb=250mm×600mm(石灰水粉刷)。各层墙顶均设截面为190mm×190mm的钢筋混凝土圈梁。



    计算弯矩系数αM=0.450，计算轴力系数ηN=1.450，则托梁跨中截面的弯矩Mb和轴心拉力Nb与下列( )组数据最为接近。

    A..347.7kN·m；238.6kN
    B..354.27kN·m；239.7kN
    C..365kN·m；245.6kN
    D..372.35kN·m；318.92kN

    答案：A
    解析：

  • 第15题：

    对某钢筋混凝土简支T梁桥进行承载能力评定，该桥计算跨径为20.0m，桥面横向布置为0.3m（栏杆）+9.0m（车行道）+0.3m（栏杆）=9.6m，无人行道，设计荷载等级为公路-Ⅱ级。根据前期检测结果得到的跨中截面正弯矩计算结果和各分项检算系数见下表。（3）根据表中数据，跨中截面正弯矩实际抗力效应R的计算结果应为（ ）。

    A.4848.6kN.m
    B.5103.8kN.m
    C.4329.2kN.m
    D.843.0kN.m

    答案：C
    解析：
    实际抗力效应R=4900×0.93×（1-0.05）=4329.2（kN.m）

  • 第16题：

    整体箱梁桥静载试验，某截面的设计活载弯矩为490kN·m（不考虑冲击），计算试验弯矩为540kN·m，冲击系数为0.10，则该截面的静力荷载效率为（ ）。

    A.0.90
    B.1.00
    C.1.05
    D.1.10

    答案：B
    解析：
    静载试验效率ηq按下式计算：ηq=SS/[S×（1+μ）式中：SS-静载试验荷载作用下，某一加载试验项目对应的加载控制截面内力或位移的最大计算效应值；S-控制荷载产生的同一加载控制截面内力或位移的最不利效应计算值；μ-按规范取用的冲击系数值。

  • 第17题：

    二级公路上的一座永久性桥梁，为单孔30m跨径的预应力混凝土T形梁结构，全宽12m，其中行车道净宽9.0m，两侧各附1.5m的人行道。横向由5片梁组成，主梁计算跨径29.16m，中距2.2m。结构安全等级为一级。设计汽车荷载为公路-I级，人群荷载为3.5kN/m2，由计算知，其中一片内主梁跨中截面的弯矩标准值为：总自重弯矩2700kN·m，汽车作用弯矩1670kN·m，人群作用弯矩140kN·m。试问，该片梁的作用效应基本组合的弯矩设计值（kN·m）与下列何项数值最为接近？（　　）

    A.4500
    B.5800
    C.5700
    D.6300

    答案：D
    解析：

  • 第18题：

    某高速公路立交匝道桥为一孔25.8m预应力混凝土现浇简支箱梁，桥梁全宽9m，桥面宽8m，梁计算跨径25m，冲击系数0.222，不计偏载系数，梁自重及桥面铺装等恒载作用按154.3kN/m计，如题图，试问：桥梁跨中弯矩基本组合值（kN·m），与下列何项数值最为接近（　　）



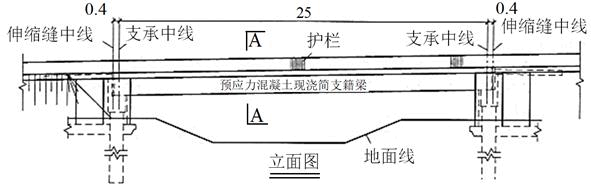
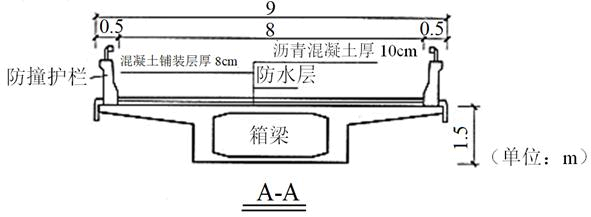    A． 23900
    B． 24400
    C． 25120
    D． 26290

    答案：D
    解析：
    根据《公路桥涵设计通用规范》（JTG D60—2015）第4.3.1条第3款表4.3.1-1，查表4.3.1-1得：高速公路汽车荷载等级采用公路—Ⅰ级。
    根据4.3.1条第4款第1项规定，公路—Ⅰ级车道荷载均布荷载标准值为qk＝10.5kN/m，集中荷载标准值Pk取值见表4.1.3-2。计算剪力效应时，上述集中荷载标准值应乘以系数1.2。
    故车道荷载：qk＝10.5kN/m。
    集中荷载：Pk＝2（L0＋130）＝2×（25＋130）＝310kN。
    根据表4.3.1-4规定，桥涵设计车道数，桥面宽度8m，故桥涵设计车道数取2。
    根据表4.3.1-5规定，横向车道数取2道，故横向车道布载系数取1.0。
    根据表4.3.1-6规定，纵向折减系数不予折减。
    根据第4.1.5条式（4.1.5-1）计算，分别求出永久作用、汽车作用标准值。
    恒载作用跨中弯矩标准值：MGk＝（1/8）×154.3×252＝12055kN·m
    双车道汽车作用跨中弯矩标准值：M1k＝M1kq＋M1kp
    M1kq＝2×（1/8）×10.5×252＝1641kN·m
    M1kp＝2×（1/4）×310×25＝3875kN·m
    M1k＝1641＋3875＝5516kN·m
    根据表4.1.5-1，高速公路设计安全等级为一级，故结构重要性系数取1.1。
    根据表4.1.5-2，永久作用分项系数取1.2。
    根据第4.1.5条第1款，汽车荷载车道荷载计算取分项系数1.4。
    跨中弯矩基本组合为：
    Mud＝1.1×[1.2×MGk＋1.4×（1＋μ）×M1k]＝1.1×[1.2×12055＋1.4×1.222×5516]＝26293kN·m

  • 第19题：

    复杂截面极件静载强度计算中，如果极件同时受弯矩M和轴向力N，且τm和τN方向相同，则合成应力τ合与它们的关系是（）

    • A、τ合=τm-τN
    • B、τ合=τm+τN
    • C、τ合=τm-τN
    • D、τ合=τm×τN

    正确答案:B

  • 第20题：

    若按弹性理论计算的弯矩Me＝100kN·m，取弯矩调幅系数β关为0.2，则调幅后的弯矩Ma为：（）

    • A、20kN·m
    • B、80kN·m
    • C、83.3kN·m
    • D、120kN·m

    正确答案:B

  • 第21题：

    单选题
    托梁按偏心受拉构件进行计算，若已知αM=0.250，ηN=2.032，as=as′=45mm，假设墙梁的跨中计算高度H0=5.450m，由荷载Q2引起的跨中弯矩值M2=315kN·m，则轴心力至纵向钢筋合力点之间的距离e（mm）与（　　）项数值最为接近。
    A

    670

    B

    550

    C

    490

    D

    450


    正确答案： C
    解析：
    由题意可知，跨中最大弯矩设计值为：Mb=αMM2=0.250×315=78.75kN·m，根据《砌体结构设计规范》（GB 50003—2011）第7.3.6条式（7.3.6-2）计算，轴心拉力设计值为：Nbt=ηN M2/H0=2.032×315/5.450=117.45kN；
    e0=Mbt/Nbt=0.67m>0.5（hb-as-a′s）=0.5×（0.45-2×0.045）=0.18m，
    为大偏心受拉构件，轴心力至纵向钢筋合力点之间的距离为：
    e=e0-h/2+as=670-450/2+45=490mm。由此可知，C项数值最为接近。

  • 第22题：

    单选题
    若按弹性理论计算的弯矩Me＝100kN·m，取弯矩调幅系数β关为0.2，则调幅后的弯矩Ma为：（）
    A

    20kN·m

    B

    80kN·m

    C

    83.3kN·m

    D

    120kN·m


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    计算弯矩系数αM＝0.450，计算轴力系数ηN＝1.450，则托梁跨中截面的弯矩Mb和轴心拉力Nb与下列（　　）组数据最为接近。
    A

    347.7kN·m；238.6kN

    B

    354.27kN·m；239.7kN

    C

    365kN·m；245.6kN

    D

    372.35kN·m；318.92kN


    正确答案： B
    解析：
    由题可知，M1＝Q1l02/8＝23.8×6.052/8＝108.89kN·m；M2＝Q2l02/8＝116×6.052/8＝530.74kN·m。
    根据《砌体结构设计规范》（GB 50003—2011）第7.3.6条式（7.3.6-1）规定，托梁跨中截面的弯矩为：
    Mb＝M1＋αMM2＝108.89＋0.450×530.74＝347.72kN·m
    根据第7.3.6条式（7.3.6-2）计算，轴心拉力为：Nb＝ηNM2/H0＝1.45×530.74/3.225＝238.63kN。
    选项中与结果最接近的是347.7；238.6，因此答案选A项。

  • 第24题：

    单选题
    确定使用阶段墙梁在其恒荷载设计值和活荷载设计值最不利布置下托梁跨中弯矩Mb1及轴力Nb1、支座B的负弯矩设计值MbB与下列（　　）组数值最为接近。
    A

    Mb1＝94.55kN·m；Nb1＝94.62kN；MbB＝－193.00kN·m

    B

    Mb1＝105.34kN·m；Nb1＝98.65kN；MbB＝－235.63kN·m

    C

    Mb1＝108.34kN·m；Nb1＝98.65kN；MbB＝－269.85kN·m

    D

    Mb1＝151.89kN·m；Nb1＝94.62kN；MbB＝－269.85kN·m


    正确答案： D
    解析：
    托梁在其顶面恒荷载及活荷载量不利布置作用下跨中弯矩（近似计算）为：
    M1＝α1Q1gl02＋α2Q1pl02＝0.07×19.548×5.302＋0.096×9.24×5.302＝63.35kN·m
    式中，α1、α2为连续梁弯矩系数；近似取恒荷载及活荷载分别作用下的跨中最大弯矩。
    中间支座最大弯矩为：M1B＝－0.125×（19.548＋9.24）×5.302＝－101.08kN·m。
    求墙梁顶面荷载作用下连续梁跨中及支座最大弯矩M2、M2B为：
    M2＝0.07×52.85×5.302＋0.096×12.47×5.302＝137.55kN·m
    M2B＝－0.125Q2l02＝－0.125×（52.85＋12.47）×5.302＝－229.35kN·m
    考虑墙梁组合作用的托梁跨中弯矩系数为：
    αM＝ψM（2.7hb/l0－0.08）＝1.0×（2.7×0.6/5.3－0.08）＝0.226
    考虑墙梁组合作用的托梁跨中轴力系数为：ηN＝0.8＋2.6hw/l0＝0.8＋2.6×3.00/5.30＝2.27。
    托梁跨中截面弯矩Mb1、Mb2和轴力Nb1、Nb2为：Mb1＝Mb2＝M＋αMM2＝63.35＋0.226×137.55＝94.45kN·m；Nb1＝Nb2＝ηNM2/H0＝2.27×137.55/3.3＝94.62kN。
    αM＝0.4（无洞口），托梁中间支座截面弯矩为：MbB＝M1B＋αMM2B＝－101.08－0.4×229.35＝－192.82kN·m。
    选项中与结果最接近的是94.55、94.62、－193.00，因此答案选A项。

相关内容