单选题某保单的理赔次数N服从参数为Λ的泊松分布，已知Λ又服从均值为1/4的指数分布，则该保单组合至少发生一次理赔的概率为（　　）。A 0.10B 0.15C 0.20D 0.55E 0.80

题目
单选题
某保单的理赔次数N服从参数为Λ的泊松分布，已知Λ又服从均值为1/4的指数分布，则该保单组合至少发生一次理赔的概率为（　　）。
A

0.10

B

0.15

C

0.20

D

0.55

E

0.80

相似考题

1.已知随机变量 X 服从参数为 λ 的泊松分布,且 P(X=2)=P(X=4),则 λ=2. ()此题为判断题(对，错)。

2.随机变量X服从参数为λ的泊松分布,且D(X)=2,则P{X=1}=()。

3.随机变量X服从参数为的λ泊松分布,则X的分布列为();若E(X－1)(X－2)=1,则λ=()。

4.设随机变量X1,X2,…,X100相互独立且都服从参数为4的泊松分布,则它们的算术平均值小于等于4.392的概率为()。A、0.975B、0.95C、0.875D、0.825

更多“单选题某保单的理赔次数N服从参数为Λ的泊松分布，已知Λ又服从均值为1/4的指数分布，则该保单组合至少发生一次理赔的概率为（　　）。A 0.10B 0.15C 0.20D 0.55E 0.80”相关问题

  • 第1题：

    关于泊松分布，错误的有

    A、二项分布中，n很大，π根小，则可用泊松分布近似二项分布

    B、泊松分布由均数唯一确定

    C、泊松分布的均数越大，越接近正态分布

    D、泊松分布的均数与标准差相等

    E、如果x1服从均数为μ1的泊松分布，x2服从均数为μ2的泊松分布，则x1＋x2服从均数为μ1＋μ2的泊松分布


    参考答案：C

  • 第2题：

    设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。

    A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布

    B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布

    C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布

    D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布


    正确答案：D
    解析：中心极限定理指出，无论共同的分布是什么，只要随机变量的个数n相当大时，的分布总近似于正态分布。

  • 第3题：

    设总体X服从参数为2的指数分布，X1，X2，…，Xn为来自总体X的简单随机样本，则当n→∞时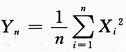，依概率收敛于_______.


    答案：
    解析：
    本题是数三的考题，根据切比雪夫大数定律或者辛钦大数定律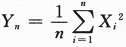，依概率收敛于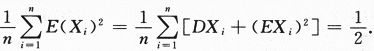答案应填

  • 第4题：

    设随机变量X服从参数为1的泊松分布,则P{X=EX^2}=________.


    答案：
    解析：
    X～P(λ)，则有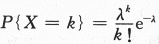，k=0，1，2，…且E(X)=λ，D(X)=λ，现λ=1，直接代入即可.
    【求解】E(X^2)=D(X)+［E(X)］^2=1+1=2，所以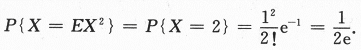

  • 第5题：

    设随机变量X服从参数为λ的泊松（Poisson）分布，且已知E[（X-1）（X-2）]=1＝1，则λ=（）。


    正确答案:1

  • 第6题：

    排队模型M/M/1/C/N指的是顾客到达服从参数为λ的，服务时间服从参数为μ的个服务台，系统容量为（）。

    • A、泊松分布负指数分布CN
    • B、泊松分布泊松分布CN
    • C、负指数分布负指数分布NC
    • D、泊松分布负指数分布NC

    正确答案:A

  • 第7题：

    设X服从0—1分布，P=0.6，Y服从λ=2的泊松分布，且X，Y独立，则X+Y（）.

    • A、服从泊松分布
    • B、仍是离散型随机变量
    • C、为二维随机向量
    • D、取值为0的概率为0

    正确答案:B

  • 第8题：

    填空题
    设离散型随机变量X服从于参数为λ（λ＞0）的泊松分布，已知P{X＝1}＝P{X＝2}，则λ＝____。

    正确答案： 2
    解析：
    根据题意λe－λ/1!＝λ2e－λ/2!，得λ＝2。

  • 第9题：

    单选题
    冰箱门体上的划伤缺陷每100台中，服从均值为10的泊松分布，则每10台冰箱的门体划伤缺陷服从（）
    A

    均值为1的泊松分布

    B

    均值为10的泊松分布

    C

    均值为100的泊松分布

    D

    以上都不正确


    正确答案： D
    解析： 暂无解析

  • 第10题：

    单选题
    排队模型M/M/1/C/N指的是顾客到达服从参数为λ的，服务时间服从参数为μ的个服务台，系统容量为（）。
    A

    泊松分布负指数分布CN

    B

    泊松分布泊松分布CN

    C

    负指数分布负指数分布NC

    D

    泊松分布负指数分布NC


    正确答案： B
    解析： 暂无解析

  • 第11题：

    问答题
    7.一电话交换台每分钟收到的呼唤次数服从参数为4的泊松分布，求 (1)每分钟恰有8次呼唤的概率； (2)每分钟的呼唤次数大于10的概率．

    正确答案：
    解析：

  • 第12题：

    单选题
    已知某风险的总理赔额随机变量服从参数为3的泊松分布，个别理赔额服从均值为1的指数分布，保险人决定购买比例再保险，安全附加系数为0.25，再保险人的附加保费率为0.20，再保险比例为40%，则原保险人在购买再保险后的调节系数为（　　）。
    A

    0.07

    B

    0.35  

    C

    0.61  

    D

    0.79  

    E

    0.87


    正确答案： B
    解析：
    设θ为原保险人安全附加系数，β为再保险人安全附加系数，α为再保险的比例系数，则θ=0.25，β=0.20，α=40%；且λ=3，P1=1。
    由于原保险人购买了再保险，所以原保险人对自己所承担的风险相应的保费为原保费与再保费之差，即：
    Cy=（1＋θ）P1λ－（1＋β）（1－α）P1λ
    =[（1＋θ）－（1＋β）（1－α）]P1λ，
    =[1＋0.25－（1＋0.20）（1－40%）]×3
    =1.59。
    又调节系数方程为：λ+Cyr=λMY（r），
    其中MY（r）为自留风险随机变量的矩母函数，且
    MY（r）=E（e40%Xr）=Mx（0.4r）=（1-0.4r）-1
    故调节系数方程即为：3+1.59r=3×（1－0.4r）-1。
    解得：r=0.61。

  • 第13题：

    在某事件的每次实验中，设成功的概率为P，则失败的概率为Q（＝1-P），在n次实验中，该事件成功k次的概率为Pn（k）＝CnkPk（1-P）n-k，问成功次数k服从什么分布

    A、泊松分布

    B、二项分布

    C、正态分布

    D、F分布

    E、超儿何分布


    参考答案：B

  • 第14题：

    设Xi (i=1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。

    A．若Xi (i=1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布

    B．若Xi (i=1，2，…，n)服从指数分布，且λ相同，则服从正态分布

    C．若Xi(i=1，2，…，n)服从[a，b)上的均匀分布，则服从正态分布

    D．无论Xi (i=1，2，…，n)服从何种分布，其均值都服从正态分布


    正确答案：A
    解析：若总体服从正态分布，无论样本量大小，其样本均值X都服从正态分布。

  • 第15题：

    随机变量X与Y相互独立，X服从参数为1的指数分布，Y的概率分布为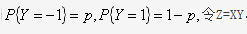。求Z的概率密度


    答案：
    解析：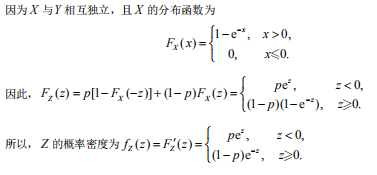

  • 第16题：

    冰箱门体上的划伤缺陷每100台中，服从均值为10的泊松分布，则每10台冰箱的门体划伤缺陷服从（）

    • A、均值为1的泊松分布
    • B、均值为10的泊松分布
    • C、均值为100的泊松分布
    • D、以上都不正确

    正确答案:A

  • 第17题：

    考虑某门诊医疗保险计划，已知每个人每年的门诊理赔次数服从均值为3的泊松分布，现将齿科门诊从该医疗保险计划中去除。根据历史数据，齿科门诊发生概率为15%，则对去除齿科门诊保险以后的保险计划，每人每年门诊理赔2次的概率为（）。

    • A、0.1350
    • B、0.2539
    • C、0.4751
    • D、0.5256
    • E、0.6183

    正确答案:B

  • 第18题：

    某段高速公路每周发生交通事故的次数服从参数为λ=3的泊松分布，则该段高速公路每周发生4次交通事故的概率为（）。（取e-3≈0.0498）


    正确答案:0.168075

  • 第19题：

    问答题
    X服从参数为2的指数分布，Y服从参数为4的指数分布，则E(2X2+3Y)=____ .

    正确答案：
    解析：

  • 第20题：

    单选题
    考虑某门诊医疗保险计划，已知每个人每年的门诊理赔次数服从均值为3的泊松分布，现将齿科门诊从该医疗保险计划中去除。根据历史数据，齿科门诊发生概率为15%，则对去除齿科门诊保险以后的保险计划，每人每年门诊理赔2次的概率为（）。
    A

    0.1350

    B

    0.2539

    C

    0.4751

    D

    0.5256

    E

    0.6183


    正确答案： D
    解析： 暂无解析

  • 第21题：

    单选题
    一组一年期的定期寿险组合，每份保单的保险金额都为B个单位元，索赔次数N服从泊松分布，参数为λ，则下列计算中不正确的是（　　）。
    A

    E（S）=E（N）B=λB

    B

    Var（S）=Var（N）B2=λB2

    C

    S的可能取值为0，B，2B，…

    D

    E（X）=B，Var（X）=B2

    E

    P（S≤BX）=P（N≤X）


    正确答案： B
    解析：
    记X为每份保单的索赔金额，由已知条件得：E（X）=E（B）=B，Var（X）=Var（B）=0；E（N）=Var（N）=λ。
    故由聚合风险模型得：
    ①E（S）=E（N）E（X）=λB；
    ②Var（S）=E2（X）Var（N）+E（N）Var（X）=B2λ；
    ③由于每次理赔额均为常数B，所以在保险期内索赔总额仅取B的倍数，即0，B，2B，…；
    ④依题意有：P（X=B）=1，E（X）=B，Var（X）=0；
    ⑤由于S=BN，所以P（S≤BX）=P（BN≤BX）=P（N≤X）。

  • 第22题：

    单选题
    某保险公司承保工伤医疗保险。已知每月的理赔次数N服从参数为10的泊松分布，且每次发生的理赔都与其他理赔是相互独立的。每次理赔事件中理赔额有5%的可能超过20000元。则半年内至少有2次理赔的理赔额超过20000元的概率等于（　　）。
    A

    1-6e-5

    B

    1-4e-3

    C

    1-3e-2

    D

    1-2e-1

    E

    1-1.5e-0.5


    正确答案： A
    解析：
    设每月理赔额超过20000元的次数为N*，则
    N*＝I1+…+IN，P（I=1）＝1-P（I＝0）=v，v＝P（X＞20000）＝0.05，
    因此，N*是泊松分布与二项分布B（1，v）的复合。
    MN*（z）＝MN［lnMI（z）］
    ＝exp/{λ×［MI（z）-1］/}
    ＝exp/{λ×［（（1-v）+vez）-1］/}
    ＝exp/{10×［（0.95+0.05ez）-1］/}
    ＝exp/{10×（0.05ez-0.05）/}
    ＝exp/{0.5×（ez-1）/}，
    即N*服从参数为0.5的泊松分布。
    由泊松分布的可加性可推知，每半年的理赔额超过20000元的次数服从参数为0.5×6=3的泊松分布。则半年内至少有2次理赔的理赔额超过20000元的概率为
    P（N≥2） =1-P（N＝0）-P（N＝1）
    =1-e-3-3e-3
    =1-4e-3

  • 第23题：

    填空题
    设随机变量X服从参数为λ的泊松分布，且已知E[（X－1）（X－2）]＝1，则λ＝____。

    正确答案： 1
    解析：
    E[（X－1）（X－2）]＝E（X2）－3E（X）＋2＝D（X）＋[E（X）]2－3E（X）＋2＝λ＋λ2－3λ＋2＝1，解得λ＝1。

相关内容