多选题设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（　　）。[2008年真题]AP（X=2）=0.027BP（X=0）=0CP（X≤1）=0.972DP（X＜3）＝1EP（0≤X≤3）=1

题目
多选题
设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（　　）。[2008年真题]
A

P（X=2）=0.027

B

P（X=0）=0

C

P（X≤1）=0.972

D

P（X＜3）＝1

E

P（0≤X≤3）=1

相似考题

1.设a=3,则执行x=Iif(a>5,－1,0)后,x的值为( )A.5B.6C.0D.－－1设a=3，则执行x=Iif(a>5,-1,0)后，x的值为( )A.5B.6C.0D.--1

2.设f(x)=(x-1)(x-2)(x-3)，则方程f′(x)=0在(0，3)内的根的个数为(56)。A．1B．2C．3D．4

3.设一批产品的不合格品率为0.1，从中任取3件，记x为其中的不合格品数，下列概率计算正确的有（ ）。A.P(X=2)=0.027B.P(X=O)=0C.P(X≤1)=0.972D.P(X<3)=1E.P(0≤X≤3)=1

4.设f(x)=x(x＋1)(x＋2)(x＋3),则f'(x)=0的正根的个数为()A、0B、1C、2D、3

更多“多选题设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（　　）。[2008年真题]AP（X=2）=0.027BP（X=0）=0CP（X≤1）=0.972DP（X＜3）＝1EP（0≤X≤3）=1”相关问题

  • 第1题：

    产品上有缺陷就是不合格品,产品上的缺陷数X是随机变量,设产品上有x个缺陷的概率为:P(X=x)=1/2x+1,x=0,1,2,…,则该种产品的合格品率为________。

    A．1/8

    B．1/4

    C．1/2

    D．1


    正确答案：C

  • 第2题：

    盒子中有5个产品，其中恰有3个合格品．从盒子中任取2个，记X为取出的合格品个数．求
    (1)X的概率分布；
    (2)EX．


    答案：
    解析：

    则X的分布律为

  • 第3题：

    设总体X的概率密度为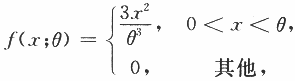其中θ∈(0,+∞)为未知参数，X1，X2，X3为来自总体X的简单随机样本，令T=max(X1，X2，X3).
    　　(Ⅰ)求T的概率密度；
    　　(Ⅱ)确定a，使得aT为θ的无偏估计.


    答案：
    解析：

  • 第4题：

    一批产品的不合格品率为0. 2，现从这批产品中随机取出5个，记X为这5个产品中的不合格品数，则这5个产品中没有不合格品的概率为（ ）。



    答案：B
    解析：

  • 第5题：

    在一个制造过程中，不合格率为0. 05，如今从成品中随机取出10个，记X为10个成品中的不合格品数，恰有一个不合格品的概率P（X = 1）=（）。
    A. -0.05 B. 0. 125 C. 0.315 D. 1.05


    答案：C
    解析：

  • 第6题：

    设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（）。
    A. P(X=2)=0.027 B. P(X=0)=0
    C. P(X≤1)=0. 972 D. P(XE. P(0≤X≤3) = 1


    答案：A,C,E
    解析：

  • 第7题：

    设二维随机变量（X，Y）在区域D上服从均匀分布，其中D://0≤x≤2，0≤y≤2。记（X，Y）的概率密度为f（x，y），则f（1，1）=（）


    正确答案:0.25

  • 第8题：

    多选题
    设X～N（0，1），则下列各式成立的有（　　）。
    A

    P（X＞a）=P（X≥a）=1-Φ（a）

    B

    P（a≤X≤b）=Φ（b）-Φ（a）

    C

    P（｜X｜≤a）=2Φ（a）-1

    D

    Φ（-a）=-Φ（a）

    E

    P（X＜a）=P（X≥a）=1-Φ（a）


    正确答案： A,C
    解析：
    对于标准正态分布有Φ（-a）=1-Φ（a），P（X＜a）=Φ（a），P（X≥a）=1-Φ（a）。

  • 第9题：

    多选题
    设随机变量X的分布列如表所示，下列概率计算中正确的有（　　）。[2008年真题]
    A

    P（4＜X＜5）=0.9

    B

    P（X＜4）=0.1

    C

    P（X＜6）=1

    D

    P（X≥5）=0

    E

    P（4＜X≤5）=0.6


    正确答案： B,A
    解析： P（4＜X＜5）=0；P（X＜4）=P（X=3）=0.1；P（X＜6）=P（X=3）+P（X=4）+P（X=5）=1；P（X≥5）=P（X=5）=0.6；P（4＜X≤5）=P（X=5）=0.6。

  • 第10题：

    多选题
    设x～N(0，1)，则下列各式成立的有(　　)。
    A

    P(X>a)=P(X≥a)=φ(a)

    B

    P(a≤X≤b)=φ(b)-φ(a)

    C

    P(|X|≤a)=2φ(a)-1

    D

    φ(-a)=-φ(a)

    E

    φ(-a)=2φ(a)<br /><span></span>


    正确答案： A,B
    解析： 暂无解析

  • 第11题：

    多选题
    设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（　　）。[2008年真题]
    A

    P（X=2）=0.027

    B

    P（X=0）=0

    C

    P（X≤1）=0.972

    D

    P（X＜3）＝1

    E

    P（0≤X≤3）=1


    正确答案： E,A
    解析： 不合格品数X有四种可能，则其概率分别为:P（X=0）=0.9×0.9×0.9=0.729；P（X=1）=3×0.1×0.9×0.9=0.243；P（X=2）=3×0.1×0.1×0.9=0.027；P（X=3）=0.1×0.1×0.1=0.001。所以，P（X≤1）=P（X=0）+P（X=1）=0.972，P（0≤X≤3）= P（X=0）+P（X=1）+P（X=2）+P（X=3）=1。

  • 第12题：

    单选题
    设X～N（2，22），其概率密度函数为f（x），分布函数F（x），则（　　）。
    A

    P{X≤0}＝P{X≥0}＝0.5

    B

    f（－x）＝1－f（x）

    C

    F（x）＝－F（－x）

    D

    P{X≥2}＝P{X＜2}＝0.5


    正确答案： B
    解析：
    该正态分布的密度函数的图像关于x＝μ＝2对称，故P{X≥2}＝P{X＜2}＝0.5，故应选D。

  • 第13题：

    一批产品的不合格品率为0.2，现从这批产品中随机取出5个，记X为这5个产品中的不合格品数，则这5个产品中没有不合格品的概率为( )。


    正确答案：B
    解析：

  • 第14题：

    设X~U(0，1)，从中取到一个样本量为12的随机样本X1,X2,…,X12,令Y = X1 + X2 +…+X12-6，则下列结论正确的有（ ）。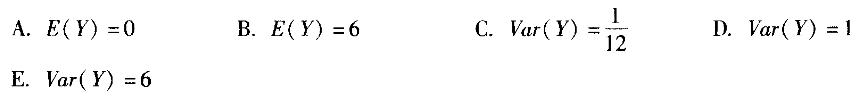


    答案：A,D
    解析：

  • 第15题：

    设随机变量X的概率密度为

    ，则有( )。


    A、E(X)=0，D(X)=1
    B、E(X)=0，D(X)=2
    C、E(X)=0，D(X)=3
    D、E(X)=1，D(X)=2

    答案：B
    解析：

  • 第16题：

    某批产品批量1 000件，不合格品率P=10%，从该批产品中抽取10件，其中不合格品数不超过1件的概率为（）。
    A. 0. 910 B. 1. 9X0. 99

    C. 0. 99 D. 1. 9X0. 910


    答案：B
    解析：
    。记10件产品中的不合格数为X，则P(X≤1) = P(X=1)+P(X=0) = 10X 0. 99 ×0. 1+0. 910 = 1. 9×0. 99。

  • 第17题：

    设一批产品的不合格品率为0.1，从中任取3件，记X为其中的不合格品数，则下列概率计算正确的有（ ）。[2008年真题]
    A. P(X=2) =0.027 B. P(X=0) =0
    C. P(X ≤l) =0.972 D. P(XE. P(0 ≤X ≤3) =1


    答案：A,C,E
    解析：
    不合格品数X有四种可能，则其概率分别为：P(X=0) =0.9×0.9×0.9 =0.729; P(X = l) = 3×0. 1×0. 9×0. 9 = 0. 243 ； P(X = 2) =3×0. 1×0. 1×0.9 =0.027； P(X =3) =0. 1×0. 1×0. 1 =0.001。所以，P(X≤l) =P(X=0) +P(X=1) =0. 972, P(0≤X≤ 3) = P(X = 0) +P(X = 1) +P(X = 2) +P(X=3) =1。

  • 第18题：

    设随机变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2服从正态分布N（0，22），X3服从参数为λ=3的泊松分布，记Y=X1-2X2+3X3。则DY=（）。


    正确答案:46

  • 第19题：

    设随机变量X的概率分布为P{X=k}=θ（1-θ）k-1，k=1，2，L，其中0<θ<1，若P{X≤2}=5/9，则P{X=3}=（）。


    正确答案:4/27

  • 第20题：

    填空题
    设随进变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2～N（0，22），X3服从参数为λ=3的泊松分布，记随机变量Y=X1-2X2+3X3，则D（Y）=____.

    正确答案： 46
    解析：
    ∵X1～U[0，6]　　　X2～N[0，22]　　　X3～P（3）
    ∴D（X1）=62/12=3　　　D（X2）=22=4　　　D（X3）=3
    又X1，X2，X3相互独立，故
    ∴D（Y）=D（X1-2X2+3X3）=D（X1）+4D（X2）+9D（X3）=3+4×4+9×3=46

  • 第21题：

    多选题
    设X服从标准正态分布，且0＜a＜b，则下列各式成立的有（　　）。
    A

    P（X＞a）＝P（X≥a）＝1-Ф（a）

    B

    P（a≤X≤b）＝Ф（b）-Ф（a）

    C

    P（X＝a）＝0

    D

    P（-a＜X＜a）＝Ф（a）-1

    E

    P（X＝b）＝1


    正确答案： E,A
    解析： 若X服从标准正态分布，且0＜a＜b，则P（-a＜X＜a）＝Ф（a）-Ф（-a）＝Ф（a）-[1-Ф（a）]＝2Ф（a）-1；P（X＝b）＝0。

  • 第22题：

    多选题
    设X～N(0，1)，则下列各式成立的有(　　)。
    A

    P(X>a)=P(X≥a)=φ(a)

    B

    P(a≤X≤b)=φ(b)－φ(a)

    C

    P(|X|≤a)=2φ(a)－1

    D

    φ(－a)=－φ(a)

    E

    φ(－a)=2 φ(a)


    正确答案： E,A
    解析： 对于答案D，大家可以知道是错误的φ(－a)=1－φ(a)；对于答案A，表示的是图形a右边的面积应该是P(X>a)=P(X≥a)=1－φ(a)；答案B表示出了a,b与X轴和分布函数所围成曲边梯形的面积；答案C：P(|X|≤a)=1－[2 ×(1－φ(a))]=2φ(a)－1

  • 第23题：

    单选题
    设f（x）＝x（x－1）（x－2），则方程f′（x）＝0的实根个数是（　　）。[2016年真题]
    A

    3

    B

    2

    C

    1

    D

    0


    正确答案： B
    解析：
    先对方程求导，得：f′（x）＝3x2－6x＋2，再根据二元函数的判别式Δ＝b2－4ac＝12＞0，可知方程有两个实根。

  • 第24题：

    单选题
    设随机变量X1，X2，X3相互独立，其中X1在[0，6]上服从均匀分布，X2～N（0，22），X3服从参数为λ＝3的泊松分布，记随机变量Y＝X1－2X2＋3X3，则D（Y）＝（　　）。
    A

    56

    B

    48

    C

    72

    D

    46


    正确答案： B
    解析：
    ∵X1～U[0，6]，X2～N[0，22]，X3～P（3）。
    ∴D（X1）＝62/12＝3，D（X2）＝22＝4，D（X3）＝3。
    又X1，X2，X3相互独立，故D（Y）＝D（X1－2X2＋3X3）＝D（X1）＋4D（X2）＋9D（X3）＝3＋4×4＋9×3＝46。

相关内容