单选题张红是某大学一年级的学生，她参加了微积分的两次考试，第一次考试中，全班的平均成绩是75分，标准差是10分，第二次考试中，全班的平均成绩是70分，标准差是15分，张红每次考试成绩都是85分，假定考试分数近似从正态分布，则张红两次考试的成绩在班里的相对位置（　　）。[2016年中级真题]A 不相同，第一次比第二次好B 不相同，第二次比第一次好C 相同D 因为不知道班里人数而无法判斩

题目
单选题
张红是某大学一年级的学生，她参加了微积分的两次考试，第一次考试中，全班的平均成绩是75分，标准差是10分，第二次考试中，全班的平均成绩是70分，标准差是15分，张红每次考试成绩都是85分，假定考试分数近似从正态分布，则张红两次考试的成绩在班里的相对位置（　　）。[2016年中级真题]
A

不相同，第一次比第二次好

B

不相同，第二次比第一次好

C

相同

D

因为不知道班里人数而无法判斩

相似考题

1.证券从业资格证考试 我是分为两次考的,第一次3月考基础,第二次6月考交易。过了之后成绩是在一张纸上还我是分为两次考的,第一次3月考基础,第二次6月考交易。过了之后成绩是在一张纸上还是两张。

2.为了研究数学考试成绩与统计学考试成绩之间的关系,现从某大学统计系的学生中随机抽取 10 人进行调查,所得结果如下:

3.甲、乙两个班参加同一学科考试，甲班的平均考试成绩为86分，标准差为12分。乙班考试成绩的分布如下：（1）画出乙班考试成绩的直方图。（2）计算乙班考试成绩的平均数及标准差。（3）比较甲乙两个班哪个班考试成绩的离散程度大?

4.张红是某大学一年级的学生，她参加了微积分的两次考试。第一次考试中，全班的平均成绩是75分，标准差是10分；第二次考试中，全班的平均成绩是70分，标准差是15分。张红每次考试成绩都是85分。假定考试分数近似服从正态分布，则张红两次考试的成绩在班里的相对位置（ ）。A.不相同，第一次比第二次好B.不相同，第二次比第一次好C.相同D.因为不知道班里人数而无法判断

更多“张红是某大学一年级的学生，她参加了微积分的两次考试，第一次考试中，全班的平均成绩是75分，标准差是10分，第二次考试中，”相关问题

  • 第1题：

    某班有50个学生，在数学考试中，成绩是在前10名的学生的平均分比全班平均分高12分，那么其余同学的平均分比全班平均分低了多少分？（ ）

    A．3

    B．4

    C．5

    D．6


    正确答案：A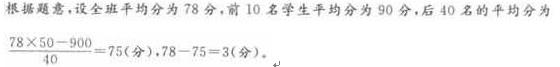

  • 第2题：

    某大学某班学生总数为32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是( )。

    A．22

    B．18

    C．28

    D．26


    正确答案：A
    A  [解析]都没有及格的有4人，则至少有一次考试及格的人数为32-4=28，两次考试及格的总人数次是26+24=50，所以两次考试都及格的人数是50-28=22，故选A。

  • 第3题：

    某班有50个学生，在数学考试中，成绩是在前10名的学生的平均分比全班平均分高12分，那么其余同学的平均分比全班平均分低了多少分？( )


    A. 3
    B. 4
    C. 5
    D. 6

    答案：A
    解析：
    解题指导： 根据题意，设全班平均分为78分，前10名学生平均分为90分，后40名的平均分为（78*50-900）/40=75分，78-75=3分。故答案为A。

  • 第4题：

    某班共有60名学生，在期末的统计学考试中，男生的平均考试成绩为75分，标准差为6分；女生的平均考试成绩为80分，标准差为6分。如果该班的男女学生各占一半，则全班的平均考试成绩为（ ）。

    A.65
    B.75．5
    C.77．5
    D.80

    答案：C
    解析：
    设男生成绩为x，女生成绩为y，男女各30人，故全班的平均考试成绩为：

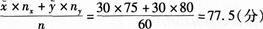
  • 第5题：

    在某次考试中，小明的语文成绩为80。已知全班语文平均成绩为65，语文成绩的标准差为10。小明语文科目的标准分数是

    A.1.5
    B.-1.5
    C.2/3
    D.15%

    答案：A
    解析：
    标准分数，又称基分数或Z分数，是以标准差为单位表示一个原始分数在团体中所处位置的相对位置量数。标准分数的公式是

    ,因此本题中小明的语文科目的标准分数是1.5。

  • 第6题：

    某学校统计学考试成绩服从正态分布，以往经验表明成绩的标准差为10分。从学生中随机抽取25个简单随机样本，他们的平均分数是84.32分。根据这些数据计算该校学生的统计学考试的平均成绩的95%的置信区间是（）

    • A、84.32±39.2
    • B、84.32±1.96
    • C、84.32±3.92
    • D、84.32±19.6

    正确答案:C

  • 第7题：

    某班级学生期末统计学考试平均成绩为82分，标准差为5分。如果已知这个班学生的考试分数服从正态分布，可以判断成绩在77-87之间的学生大约占全班学生的（）


    正确答案:68%

  • 第8题：

    某班共有60名学生，在期末的统计学考试中，男生的平均考试成绩为75分，标准差为6分；女生的平均考试成绩为80分，标准差为6分。如果该班的男女学生各占一半，则全班的平均考试成绩为（）。

    • A、75
    • B、80
    • C、77.5
    • D、无法计算

    正确答案:C

  • 第9题：

    单选题
    某班共有60名学生，在期末的统计学考试中，男生的平均考试成绩为75分，标准差为6分；女生的平均考试成绩为80分，标准差为6分。如果该班的男女学生各占一半，则金班的平均考试成绩为（）分。
    A

    75

    B

    76

    C

    77.5

    D

    78

    E

    80


    正确答案： C
    解析： 暂无解析

  • 第10题：

    单选题
    张红是某大学一年级的学生，她参加了微积分的两次考试，第一次考试中，全班的平均成绩75分，标准差10分，第二次考试中，全班的平均成绩是70分，标准差是15分，张红每次考试成绩都是85分，假定考试分数近似从正态分布，则张红两次考试的成绩在班里的相对位置（　　）。[2016年中级真题]
    A

    不相同，第一次比第二次好

    B

    不相同，第二次比第一次好

    C

    相同

    D

    因为不知道班里人数而无法判斩


    正确答案： C
    解析：
    标准分数也称标准化值或Z分数，它是变量值与其平均数的离差除以标准差后的值，用以测定某一个数据在该组数据中的相对位置。第一次考试的标准分数为（85－75）/10＝1，第二次考试的标准分数为（85－70）/15＝1。因此张红两次考试的成绩在班里的相对位置相同。

  • 第11题：

    填空题
    某班级学生期末英语考试平均成绩为75分，标准差为10分。如果已知这个班学生的考试分数服从正态分布，可以判断成绩在65-85之间的学生大约占全班学生的（）

    正确答案： 68%
    解析： 暂无解析

  • 第12题：

    填空题
    某班级学生期末统计学考试平均成绩为82分，标准差为5分。如果已知这个班学生的考试分数服从正态分布，可以判断成绩在77-87之间的学生大约占全班学生的（）

    正确答案： 68%
    解析： 暂无解析

  • 第13题：

    某大学某班学生总数是32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没及格的有4人，那么两次考试都及格的人数是(  )

    A.22        B.18       C.28      D.26


    设两次考试都及格的人数是X人,则及格人数中仅第一次及格的是26-X人,仅第二次及格的人数是24-X人.
    由题知不及格人数中仅第一次不及格的是32-26-4=2人,仅第二次不及格的是32-24-4=4人.
    仅第一次及格人数+仅第二次及格人数+两次都及格人数+仅第一次不及格人数+仅第二次不及格人数+两次都不及格人数=全班总人数,即(26-X)+(24-X)+X+2+4+4=32,得X=28

  • 第14题：

    ：某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中，都没有及格的有4人，那么两次考试都及格的人数是（ ）。

    A．22 B．18

    C．28 D．26


    正确答案：A

    由题意知第一次不及格的有6人，第二次不及格的有8人，又已知两次都不及格的人有4人，则两次考试刚好及格一次的人数为6＋8－4＝10（人），则两次都及格的人数为32－（6＋8－4）＝22（人），故答案为A。

  • 第15题：

    某班2017年中级经济师考试中，已知公共课考试的全班平均分为110分，标准差为10分，如果学生的考试分数服从正态分布，则依据经验法则，可以判断成绩在100—120分之间的学生大概占全班学生的（ ）。

    A.68％
    B.95％
    C.99％
    D.100％

    答案：A
    解析：
    100—120分与平均分的差为正负1个标准差，根据“168”即约有68％的数据与平均数的距离在1个标准差之内，选择A项。

  • 第16题：

    一位教授计算了全班20名同学考试成绩的平均数、中数和众数，发现大部分同学的考试成绩位于高分段。下面哪句话不可能正确?（　　）

    A.全班65％的同学的考试成绩高于平均数
    B.全班65％的同学的考试成绩高于中数
    C.全班65％的同学的考试成绩高于众数
    D.全班同学的考试成绩是负偏态分布

    答案：B
    解析：
    由于中数是位于最中间的数，中数将所有的数据平分为两组，一组50％的数据比中数大，另一组50％的数据比中数小。故本题的正确答案是B。

  • 第17题：

    某班有学生50人，有26人在第一次考试中得优，有21人在第二次考试中得优，有17人在两次考试中都没有得优，那么两次考试都得优的学生人数是（）

    • A、11.0
    • B、12.0
    • C、13.0
    • D、14.0

    正确答案:D

  • 第18题：

    会计从业资格各考试科目可以分两次通过，但连续两次考试没有通过，则第一次考试成绩无效。


    正确答案:错误

  • 第19题：

    期中考试中，某班级学生统计学平均成绩为80分，标准差为4分。如果学生的成绩是正太分布，可以判断成绩在72分-88分之间的学生大约占总体的（）


    正确答案:95%

  • 第20题：

    单选题
    一位教授计算了全班20个同学考试成绩的均值，中数和众数，发现大部分同学的考试成绩集中于高分段。下面哪句话不可能是正确的？（　　）
    A

    全班65%的同学的考试成绩高于均值

    B

    全班65%的同学的考试成绩高于中数

    C

    全班65%的同学的考试成绩高于众数

    D

    全班同学的考试成绩是负偏态分布


    正确答案： B
    解析：
    中数是按顺序排列在一起的一组数据中居于中间位置的数，即在这组数据中，有一半的数据比它大，有一半的数据比它小。故不可能出现一组数据中65%的数据高于中数。

  • 第21题：

    单选题
    下列事例中属于负强化的是(    )
    A

    综合考虑学生期末考试成绩及日常品德表现，陈老师为品学兼优的学生颁发“三好学生”奖状及小奖品

    B

    倪妈妈为了激励小品提高成绩，提出如果她本学期期末考试进了全班前三名，就给她买她一直想要的手机

    C

    周妈妈为了激励小茹提高成绩，提出如果她本学期期末考试没进全班前十名，就不带她出国旅游

    D

    苏妈妈为了激励小玲提高成绩，提出如果她本学期期末考试进了全班前三名，就免去她每周末洗碗的任务


    正确答案： D
    解析：

  • 第22题：

    单选题
    张红是某大学一年级的学生，她参加了微积分的两次考试，第一次考试中，全班的平均成绩75分，标准差10分，第二次考试中，全班的平均成绩是70分，标准差是15分，张红每次考试成绩都是85分，假定考试分数近似从正态分布，则张红两次考试的成绩在班里的相对位置(    )。
    A

    不相同，第一次成绩比第二次好

    B

    不相同，第二次成绩比第一次好

    C

    相同

    D

    因为不知道班级人数而无法判断


    正确答案： B
    解析：

  • 第23题：

    单选题
    （历年真题仅供参考）张红是某大学一年级的学生，她参加了微积分的两次考试。第一次考试中，全班的平均成绩是75分，标准差是10分；第二次考试中，全班的平均成绩是70分，标准差是15分。张红每次考试成绩都是85分。假定考试分数近似服从正态分布，则张红两次考试的成绩在班里的相对位置（    ）。
    A

    不相同，第一次比第二次好

    B

    不相同，第二次比第一次好

    C

    相同

    D

    因为不知道班里人数而无法判断


    正确答案： B
    解析：

相关内容