填空题设函数f（u）可微，且f′（0）＝1/2，则z＝f（4x2－y2）在点（1，2）处的全微分dz|（1，2）＝____。

题目
填空题
设函数f（u）可微，且f′（0）＝1/2，则z＝f（4x2－y2）在点（1，2）处的全微分dz|（1，2）＝____。
相似考题

1.设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。A、0B、π/2C、锐角D、钝角

2.设函数f（x）在点x=a处可导，则函数｜f（x）｜在点x=a处不可导的充分条件是（ ）A.f（a）=0且f′（a）=0 B.f（a）=0且f′（a）≠0 C.f（a）＞0且f′（a）＞ D.f（a）＜0且f′（a）＜

3.设函数f(x)具有二阶连续导数，且f(x)>0，f'(0)=0，则函数z=f(x)lnf(y)在点(0，0)处取得极小值的一个充分条件是A.Af(0)>1，f"(0)>0 B.f(0)>1，f"(0)C.f(0)0 D.f(0)

4.如果有函数定义functionf(x,y){…},那么以下正确的函数调用是()。A.f1,2B.f(1)C.f(1,2)D.f(,2)

更多“填空题设函数f（u）可微，且f′（0）＝1/2，则z＝f（4x2－y2）在点（1，2）处的全微分dz|（1，2）＝____。”相关问题

  • 第1题：

    设函数z=z(x，y)由方程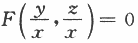确定，其中F为可微函数，且F'2≠0，则=

    A.Ax
    B.z
    C.-x
    D.-z

    答案：B
    解析：

  • 第2题：

    若函数z=f（x，y）在点P0（x0，y0）处可微，则下面结论中错误的是（　　）。



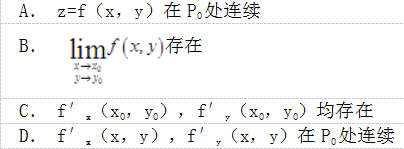    答案：D
    解析：
    二元函数z=f（x，y）在点（x0，y0）处可微，可得到如下结论：①函数在点（x0，y0）处的偏导数一定存在，C项正确；②函数在点（x0，y0）处一定连续，AB两项正确；可微，可推出一阶偏导存在，但一阶偏导存在不一定一阶偏导在P0点连续，也有可能是可去或跳跃间断点，故D项错误。

  • 第3题：

    设函数z=x2ey。则全微分dz= .


    答案：
    解析：
    【答案】dz=2xeydx+x2eydy【考情点拨】本题考查了二元函数的全微分的知识点.
    【应试指导】

  • 第4题：

    设F（X）为区间（0，3）上的单峰函数，且F（1）=2、F（2）=1.5，则可将搜索区间（0，3）缩小为（）

    • A、（0，2）
    • B、（1，2）
    • C、（2，3）
    • D、（1，3）

    正确答案:D

  • 第5题：

    设函数f(x)=丨x丨，则函数在点x=0处（）

    • A、连续且可导
    • B、连续且可微
    • C、连续不可导
    • D、不可连续不可微

    正确答案:C

  • 第6题：

    填空题
    函数f（u，v）由关系式f[xg（y），y]＝x＋g（y）确定，其中函数g（y）可微，且g（y）≠0，则∂2f/∂u∂v＝____。

    正确答案： -g′(v)/g2(v)
    解析：
    要求f（u，v）对自变量的偏导，则需将关系式f[xg（y），y]＝x＋g（y）转化为只含有u、v的关系式，故令u＝xg（y），v＝y，则x＝u/g（v），y＝v，f（u，v）＝u/g（v）＋g（v），故∂f/∂u＝1/g（v），∂2f/∂u∂v＝－g′（v）/g2（v）。

  • 第7题：

    单选题
    设函数f（u）可微，且f′（0）＝1/2，则z＝f（4x2－y2）在点（1，2）处的全微分dz|（1，2）＝（　　）。
    A

    4dx＋2dy

    B

    4dx－2dy

    C

    －4dx＋2dy

    D

    －4dx－2dy


    正确答案： A
    解析：
    求全微分，即需求出函数对各个自变量的偏导。令u＝4x2－y2，则∂z/∂x＝f′（u）·∂u/∂x＝f′（u）·8x，∂z/∂y＝f′（u）·∂u/∂y＝f′（u）·（－2y），将（1，2）代入u＝4x2－y2得u＝0，又f′（0）＝1/2，故dz|（1，2）＝f′（0）·8dx＋f′（0）·（－2·2）dy＝4dx－2dy。

  • 第8题：

    填空题
    设函数f（x）在x＝2的某邻域内可导，且f′（x）＝ef（x），f（2）＝1，则f‴（2）＝____。

    正确答案： 2e3
    解析：
    因f′（x）＝ef（x）方程两边对x求导，得f″（x）＝ef（x）·f′（x）＝ef（x）·ef（x）＝e2f（x），两边再对x求导，得f‴（x）＝e2f（x）·2f′（x）＝2e2f（x）·ef（x）＝2e3f（x）。又f（2）＝1，则f‴（2）＝2e3f（2）＝2e3。

  • 第9题：

    单选题
    设F（X）为区间（0，3）上的单峰函数，且F（1）=2、F（2）=1.5，则可将搜索区间（0，3）缩小为（）
    A

    （0，2）

    B

    （1，2）

    C

    （2，3）

    D

    （1，3）


    正确答案： C
    解析： 暂无解析

  • 第10题：

    填空题
    设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝____。

    正确答案： 2(-yf1′/x+xf2′/y)
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f1′·（－y/x2）＋f2′·（1/y），∂z/∂y＝f1′·（1/x）＋f2′·（－x/y2），x∂z/∂x－y∂z/∂y＝2（－yf1′/x＋xf2′/y）。

  • 第11题：

    单选题
    设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝（　　）。
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： D
    解析：
    根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。

  • 第12题：

    单选题
    设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    4


    正确答案： B
    解析：
    根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。

  • 第13题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第14题：

    设函数z=ln(x+y2)，则全微分dz=_______.


    答案：
    解析：

  • 第15题：

    设函数z=f（x，y）的全微分为dz=xdx+ydy，则点（0，0）（ ）《》（ ）

    A.不是f（x，y）的连续点
    B.不是f（x，y）的极值点
    C.是f（x，y）的极大值点
    D.是f（x，y）的极小值点

    答案：D
    解析：

  • 第16题：

    下列结论不正确的是（）。

    • A、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处连续
    • B、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处可导
    • C、z=f（x，y）在点（x0，y0）处可导，则f（x，y）在点（x0，y0）处可微
    • D、z=f（x，y）在点（x0，y0）处偏导数连续，则f（x，y）在点（x0，y0）处连续

    正确答案:C

  • 第17题：

    下列结论不正确的是（）。

    • A、y=f（x）在点x0处可微，则f（x）在点x0处连续
    • B、y=f（x）在点x0处可微，则f（x）在点x0处可导
    • C、y=f（x）在点x0处连续，则f（x）在点x0处可微
    • D、y=f（x）在点x0处可导，则f（x）在点x0处连续

    正确答案:C

  • 第18题：

    填空题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

    正确答案： -1/7
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第19题：

    单选题
    设函数f(x)=丨x丨，则函数在点x=0处（）
    A

    连续且可导

    B

    连续且可微

    C

    连续不可导

    D

    不可连续不可微


    正确答案： C
    解析： 暂无解析

  • 第20题：

    填空题
    设函数f（u）可微，且f′（0）＝1/2，则z＝f（4x2－y2）在点（1，2）处的全微分dz|（1，2）＝____。

    正确答案： 4dx-2dy
    解析：
    求全微分，即需求出函数对各个自变量的偏导。令u＝4x2－y2，则∂z/∂x＝f′（u）·∂u/∂x＝f′（u）·8x，∂z/∂y＝f′（u）·∂u/∂y＝f′（u）·（－2y），将（1，2）代入u＝4x2－y2得u＝0，又f′（0）＝1/2，故dz|（1，2）＝f′（0）·8dx＋f′（0）·（－2·2）dy＝4dx－2dy。

  • 第21题：

    填空题
    设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝____。

    正确答案： 1
    解析：
    根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。

  • 第22题：

    填空题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。

    正确答案： 1/sin2(sin1)
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

  • 第23题：

    填空题
    设向量u(→)＝3i(→)－4j(→)，v(→)＝4i(→)＋3j(→)，且二元可微函数f（x，y）在点P处有∂f/∂u(→)|P＝－6，∂f/∂v(→)|P＝17，则df|P＝____。

    正确答案： 10dx+15dy
    解析： {e(→)u＝{3/5，－4/5}，e(→)v＝{4/5，3/5}。由∂f/∂u(→)|P＝－6，∂f/∂v(→)|P＝17，得∂f/∂x|P×（3/5）＋∂f/∂y|P×（－4/5）＝－6，∂f/∂x|P×（4/5）＋∂f/∂y|P×（3/5）＝17，所以∂f/∂x|P＝10，∂f/∂y|P＝15。故df|P＝∂f/∂x|Pdx＋∂f/∂y|Pdy＝10dx＋15dy。

  • 第24题：

    填空题
    设单调可微函数f(x)的反函数为g(x),f(1)=3,f′(1)=2,f″(3)=6则g′(3)=（）

    正确答案： 1/2
    解析： 暂无解析

相关内容