单选题已知曲线y＝y（x）经过原点，且在原点的切线平行于直线2x－y－5＝0，而y（x）满足y″－6y′＋9y＝e3x，则y（x）等于（　　）。A sin2xB x2e2x/2＋sin2xC x（x＋4）e3x/2D （x2cosx＋sin2x）e3x

题目
单选题
已知曲线y＝y（x）经过原点，且在原点的切线平行于直线2x－y－5＝0，而y（x）满足y″－6y′＋9y＝e3x，则y（x）等于（　　）。
A

sin2x

B

x2e2x/2＋sin2x

C

x（x＋4）e3x/2

D

（x2cosx＋sin2x）e3x

相似考题

1.设某样品斑点离原点的距离为x,溶剂前沿离原点的距离为y,则Rf值为()。A、x/yB、y/xC、x/(x+y)D、y/(x+y)

2.曲线y=xlnx的平行于直线x－y＋1=0的切线方程为()。A.y=xB.y=-(x+1)C.y=(lnx)(x)D.y=x

3.intx=1,y=6;while(y－－){x＋＋;}System.out.println(x=”＋x＋y=”＋y);Whatistheresult?()A.x=6y=0B.x=7y=0C.x=6y=-1D.x=7y=-1E.Compilationfails.

4.曲线y=xlnx的平行于直线x－y＋1=0的切线方程是()A、y=xB、y=(lnx-1)(x-1)C、y=x-1D、y=-(x-1)

更多“单选题已知曲线y＝y（x）经过原点，且在原点的切线平行于直线2x－y－5＝0，而y（x）满足y″－6y′＋9y＝e3x，则y（x）等于（　　）。A sin2xB x2e2x/2＋sin2xC x（x＋4）e3x/2D （x2cosx＋sin2x）e3x”相关问题

  • 第1题：

    若方程Y=a＋bX中的截距a<0，说明A、随着X的增大，Y增大B、随着X的增大，Y减少C、随着X的减少，Y减少D、回

    若方程Y=a+bX中的截距a<0，说明

    A、随着X的增大，Y增大

    B、随着X的增大，Y减少

    C、随着X的减少，Y减少

    D、回归直线与Y轴的交点在原点下方

    E、回归直线与Y轴的交点在原点上方


    参考答案：B

  • 第2题：

    设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

    A．2x-y+2=0
    B．2x+y+1=0
    C．2x+y-3=0
    D．2x-y+3=0

    答案：D
    解析：


    @##

  • 第3题：

    曲线y=x3-4x+2在点(1，-1)处的切线方程为（　　）

    A.x-y-2-0
    B.x-y=0
    C.x+y=0
    D.x+y-2=0

    答案：C
    解析：

  • 第4题：

    设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。

    A.
    B.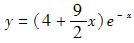
    C.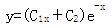
    D.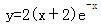

    答案：D
    解析：

  • 第5题：

    若方程Y=a+bX中的截距a<0，说明（）

    • A、随着X的增大，y增大
    • B、随着X的增大，y减少
    • C、随着X的减少，y减少
    • D、回归直线与y轴的交点在原点下方
    • E、回归直线与y轴的交点在原点上方

    正确答案:D

  • 第6题：

    已知直线经过（x1，y1）点，斜率为k（k≠0），则直线方程为（）。

    • A、y-y1=k（x-x1）
    • B、y=5kx+3
    • C、y=9k（x-x1）
    • D、y=4x+b

    正确答案:A

  • 第7题：

    填空题
    曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为____。

    正确答案： y=-exsin2x
    解析：
    所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r2－2r＋5＝0，解得r1，2＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝ex（c1cos2x＋c2sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝ex（c1cos2x＋c2sin2x）得c1＝0，c2＝－1。故所求曲线方程为y＝－exsin2x。

  • 第8题：

    单选题
    微分方程y″-6y′+9y=e3x（x+1）的特解形式应设为：（）
    A

    xe3x（ax+B.

    B

    x2e3x（ax+B.

    C

    C.e3x（ax+

    D

    ae3xx3


    正确答案： C
    解析： 暂无解析

  • 第9题：

    单选题
    已知函数y＝y（x）在任意点x处的增量Δy＝yΔx/（1＋x2）＋a，且当Δx→0时，a是Δx的高阶无穷小，y（0）＝π，则y（1）等于（　　）。
    A

    2π

    B

    π

    C

    eπ/4

    D

    πeπ/4


    正确答案： B
    解析：
    由题意可知，dy＝[y/（1＋x2）]dx，分离变量积分得ln|y|＝arctanx＋c。又y（0）＝π得c＝lnπ，故y＝earctanx＋lnπ＝πearctanx，则y（1）＝πeπ/4。

  • 第10题：

    单选题
    垂直于x轴的动直线与过原点的曲线y=y（x）（x≥0，y≥0）以及x轴围成一个以［0，x］为底边的曲边梯形，其面积为y3（x）．函数y（x）的隐函数形式是（）．
    A

    y2-x=0

    B

    y2+x=0

    C

    3y2-2x=0

    D

    2y-3x2=0


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    I＝∮L（－ydx＋xdy）/（x2＋y2），因为∂Q/∂x＝∂P/∂y＝（y2－x2）/（x2＋y2）2，所以（　　）。
    A

    对任意闭曲线L，I＝0

    B

    在L为不含原点在内的闭区域的边界线时I＝0

    C

    因为∂Q/∂x＝∂P/∂y在原点不存在，故对任意L，I≠0

    D

    在L含原点在内时I＝0，不含原点时I≠0


    正确答案： D
    解析：
    考察对于格林公式的使用条件的应用。在题设中，有∂Q/∂x＝∂P/∂y，但当原点在L内时，由于P、Q不满足在单连通域内有一阶连续偏导数的条件，故只有原点在D外时，曲线积分才与路径无关，此时I＝0。

  • 第12题：

    单选题
    曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（　　）。
    A

    y＝excos2x

    B

    y＝－excos2x

    C

    y＝exsin2x

    D

    y＝－exsin2x


    正确答案： A
    解析：
    所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r2－2r＋5＝0，解得r1，2＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝ex（c1cos2x＋c2sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝ex（c1cos2x＋c2sin2x）得c1＝0，c2＝－1。故所求曲线方程为y＝－exsin2x。

  • 第13题：

    微分方程y"-6y'+ 9y=0，在初始条件y' x=0=2,y x=0=0下的特解为：
    A. (1/2)xe2x+c B. (1/2)xe3x+c
    C. 2x D. 2xe3x


    答案：D
    解析：
    提示:先求出二阶常系数齐次方程的通解，代入初始条件，求出通解中的c1、c2值， 得特解。

  • 第14题：

    已知y=ax3在点x=1处的切线平行于直线y=2x-1，则a=______．


    答案：
    解析：
    填2/3．因为

  • 第15题：

    若方程Y=a+bX中的截距a＜0，说明

    A.随着X的增大，y减少
    B.随着X的减少，y减少
    C.随着X的增大，y增大
    D.回归直线与y轴的交点在原点上方
    E.回归直线与y轴的交点在原点下方

    答案：E
    解析：

  • 第16题：

    过点(4，-1，3)且平行于直线L：(x-3)/2=y=(z-1)/5的直线方程为( ).

    A.(x-4)/2=(y+1)/0=(z-3)/5
    B.(x-4)/2=(y+1)/1=(z-3)/5
    C.(x+4)/2=(y-1)/0=(z+3)/5
    D.(x+4)/2=(y-1)/1=(z+3)/5

    答案：B
    解析：

  • 第17题：

    微分方程y″-6y′+9y=e3x（x+1）的特解形式应设为：（）

    • A、xe3x（ax+B.
    • B、x2e3x（ax+B.
    • C、C.e3x（ax+
    • D、ae3xx3

    正确答案:B

  • 第18题：

    单选题
    已知曲线y＝y（x）经过原点，且在原点的切线平行于直线2x－y－5＝0，而y（x）满足y″－6y′＋9y＝e3x，则y（x）等于（　　）。
    A

    sin2x

    B

    x2e2x/2＋sin2x

    C

    x（x＋4）e3x/2

    D

    （x2cosx＋sin2x）e3x


    正确答案： C
    解析：
    曲线所满足的非齐次微分方程对应齐次方程的特征方程为λ2－6λ＋9＝0，故特征根为λ＝3（二重）。故齐次方程的通解为y0（x）＝（C1＋C2x）e3x设非齐次方程的特解为Ax2e3x，代入微分方程，可得A＝1/2，故非齐次方程的通解为y（x）＝（C1＋C2x）e3x＋x2e3x/2。又因为曲线过原点，故y（0）＝0；曲线在原点的切线平行于直线2x－y－5＝0，故y′（0）＝2。根据初值条件y（0）＝0，y′（0）＝2，可得C1＝0，C2＝2。故非齐次方程的通解为y（x）＝2xe3x＋x2e3x/2＝x（x＋4）e3x/2。故应选（C）。

  • 第19题：

    单选题
    若方程Y=a+bX中的截距a<0，说明（）
    A

    随着X的增大，y增大

    B

    随着X的增大，y减少

    C

    随着X的减少，y减少

    D

    回归直线与y轴的交点在原点下方

    E

    回归直线与y轴的交点在原点上方


    正确答案： A
    解析： 暂无解析

  • 第20题：

    单选题
    悬臂梁长度为l，取自由端为坐标原点，则求梁的挠曲线时确定积分常数的边界条件为（）。
    A

    x=0、y=0；x=0、y¢=0

    B

    x=l、y=0；x=l、y¢=0

    C

    x=0、y=0；x=l、y¢=0

    D

    x=l、y=0；x=0、y¢=0


    正确答案： C
    解析： 暂无解析

  • 第21题：

    单选题
    设平面α平行于两直线x/2＝y/（－2）＝z及2x＝y＝z，且与曲面z＝x2＋y2＋1相切，则α的方程为（　　）。
    A

    4x＋2y－z＝0

    B

    4x－2y＋z＋3＝0

    C

    16x＋8y－16z＋11＝0

    D

    16x－8y＋8z－1＝0


    正确答案： A
    解析：
    由平面α平行于两已知直线可得，平面α的法向量为：n＝（2，－2，1）×（1，2，2）＝－3（2，1，－2）。设切点为（x0，y0，z0），则切点处曲面的法向量为（2x0，2y0，－1），故2/（2x0）＝1/（2y0）＝（－2）/（－1），由此解得x0＝1/2，y0＝1/4，从而z0＝x02＋y02＋1＝21/16，因此α的方程为：2（x－1/2）＋（y－1/4）－2（z－21/16）＝0，即16x＋8y－16z＋11＝0。

  • 第22题：

    单选题
    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.
    A

    （x-4）/2=（y+1）/0=（z-3）/5

    B

    （x-4）/2=（y+1）/1=（z-3）/5

    C

    （x+4）/2=（y-1）/0=（z+3）/5

    D

    （x+4）/2=（y-1）/1=（z+3）/5


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    x－y＝0

    B

    x＋y＝0

    C

    －x－y＝0

    D

    －x＋y＝0


    正确答案： C
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第24题：

    单选题
    曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（　　）。
    A

    y＝exsin2x

    B

    y＝－exsin2x

    C

    y＝exsinx

    D

    y＝－exsinx


    正确答案： B
    解析：
    所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r2－2r＋5＝0，解得r1，2＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝ex（c1cos2x＋c2sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝ex（c1cos2x＋c2sin2x）得c1＝0，c2＝－1。故所求曲线方程为y＝－exsin2x。

相关内容