填空题曲面z－ez＋2xy＝3在点（1，2，0）处的切平面方程为____。

题目
填空题
曲面z－ez＋2xy＝3在点（1，2，0）处的切平面方程为____。
相似考题

1.曲线y=x3—2x在点（1，-1）处的切线方程为 ．

2.曲面z=x2+y2在(-1，2，5)处的切平面方程是： A. 2x+4y+z=11 B. -2x-4y+z=-1 C. 2x-4y-z=-15 D.2x-4y+z=-5

3.方程表示下述哪种曲面？ A.单叶双曲面 B.双曲柱面 C.双曲柱面在平面x=0上投影 D.x=-3平面上双曲线

4.求椭球面x2+2y2+z2=4在点（1，-1，1）处的切平面方程和法线方程.

更多“填空题曲面z－ez＋2xy＝3在点（1，2，0）处的切平面方程为____。”相关问题

  • 第1题：

    曲面xyz=1上平行于x+y+z+3 =0的切平面方程是：
    A.x+y+z =0 B. x+y+z=1C.x+y+z=2 D. x+y+z=3


    答案：D
    解析：
    提示：利用两平面平行、法线向量平行、对应坐标成比例求M0坐标。

  • 第2题：

    设P为椭球面S：x^2+y^2+z^2-yz=1上的动点，若S在点P处的切平面与xOy面垂直，求点P的轨迹C，并计算曲面积分，其中∑是椭球面S位于曲线C上方的部分.


    答案：
    解析：

  • 第3题：

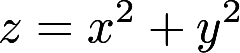    曲面 与平面 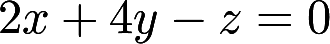平行的切平面的方程是


    答案：
    解析：

  • 第4题：

    曲线 在点 处的切线方程为______ ，法线方程为______


    答案：
    解析：

  • 第5题：

    曲面z=x2+y2-1在点(1,-1,1)处的切平面方程是( )。

    A.2x-2y-z-3=0
    B.2x-2y+z-5=0
    C.2x+2y-z+1=0
    D.2x+2y+z-1=0

    答案：A
    解析：
    设F(x,y,z)=x2+y2-z-1，则点(1,-1,1)处的切平面法向量为n=(Fx,Fy,Fz)(1,-1,1)={2x,2y,-1)(1,-1,1)={2,-2,-1)，利用平面的点法式方程公式即可得解

  • 第6题：

    曲面z=1-x2-y2在点(1/2，1/2，1/2)处的切平面方程是:

    A.x+y+z-3/2=0
    B.x-y-z+3/2=0
    C.x-y+z-3/2=0
    D.x-y+z+3/2=0

    答案：A
    解析：
    提示 F(x,y,z)=x2+y2+z-1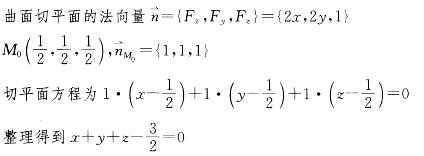

  • 第7题：

    曲面z=x2+y2在（-1，2，5）处的切平面方程是：

    A.2x+4y+z=11
    B.-2x-4y+z=-1
    C.2x-4y-z=-15
    D.2x-4y+z=-5

    答案：D
    解析：
    提示：利用点法式，求切平面方程。曲面方程写成隐函数形式x2+y2-z=0在（-1，2，5）点处，法线的方向向量为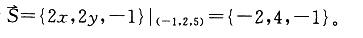

  • 第8题：

    已知曲面方程为χ2+y2+z2-2χ+8y+6z=10，则过点(5，-2，1)的切平面方程为( )。

    A、2χ+y+2z=0
    B、2χ+y+2z=10
    C、χ-2y+6z=15
    D、χ-2y+6z=0

    答案：B
    解析：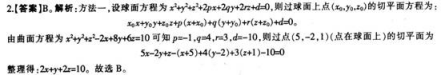

  • 第9题：

    填空题
    过x轴和点（1，－1，2）的平面方程为____。

    正确答案： 2y+z=0
    解析：
    由于所求平面经过x轴，故可设其方程为By＋Cz＝0。又由于所求平面经过点（1，－1，2），故其满足平面方程，得－B＋2C＝0，即B＝2C。故所求平面方程为2Cy＋Cz＝0，即2y＋z＝0。

  • 第10题：

    单选题
    曲面z－ez＋2xy＝3在点（1，2，0）处的切平面方程为（　　）。
    A

    4（x＋1）＋2（y－2）＝0

    B

    4（x－1）＋2（y－2）＝0

    C

    4（x－1）－2（y－2）＝0

    D

    4（x－1）＋2（y＋2）＝0


    正确答案： B
    解析：
    构造函数F（x，y，z）＝z－ez＋2xy－3，则Fx′＝2y，Fy′＝2x，Fz′＝1－ez。故将点（1，2，0）代入上式，即可得此点处切平面的法线向量为n(→)＝（4，2，0），则切平面方程为4（x－1）＋2（y－2）＝0。

  • 第11题：

    单选题
    曲面z－ez＋2xy＝3在点（1，2，0）处的切平面方程为（　　）。
    A

    3（x－1）＋2（y－2）＝0

    B

    4（x－1）＋2（y－2）＝0

    C

    3（x－1）＋（y－2）＝0

    D

    4（x－1）＋（y－2）＝0


    正确答案： A
    解析：
    构造函数F（x，y，z）＝z－ez＋2xy－3，则Fx′＝2y，Fy′＝2x，Fz′＝1－ez。故将点（1，2，0）代入上式，即可得此点处切平面的法线向量为n(→)＝（4，2，0），则切平面方程为4（x－1）＋2（y－2）＝0。

  • 第12题：

    填空题
    曲面z＝x2＋y2与平面2x＋4y－z＝0平行的切平面的方程是____。

    正确答案： 2x+4y-z-5=0
    解析：
    设曲面上有点P0（x0，y0，z0），使得曲面在此点的切平面与平面2x＋4y－z＝0平行，由曲面方程z＝x2＋y2得，曲面在P0处的法向量为（－2x0，－2y0，1），它应该与已知平面2x＋4y－z＝0的法向量n(→)＝（2，4，－1）平行，即－2x0/2＝－2y0/4＝1/（－1），解得x0＝1，y0＝2，z0＝x02＋y02＝5，故所求切平面方程为2（x－1）＋4（y－2）－（z－5）＝0，即2x＋4y－z－5＝0。

  • 第13题：

    曲面x^2+cos(xy)+yz+x=0在点(0，1，-1)处的切平面方程为

    A.Ax-y+z=-2
    B.x+y+z=0
    C.x-2y+z=-3
    D.x-y-z=0

    答案：A
    解析：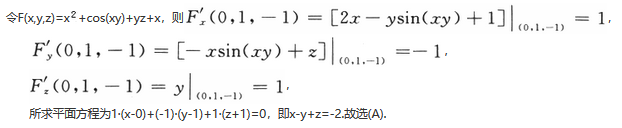

  • 第14题：

    曲面z=x(1-siny)+y^2(1-sinx)在点(1，0，1)处的切平面方程为________.


    答案：1、2x-y-z=1.
    解析：

  • 第15题：

    曲面在点的法线方程为


    答案：
    解析：

  • 第16题：

    求曲面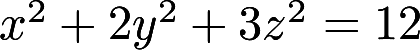 的平行于平面 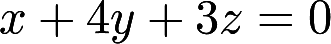的切平面方程


    答案：
    解析：

  • 第17题：

    点(-1，2，0)在平面x+2y-z+1=0上的投影是( )。



    答案：B
    解析：
    先求出过已知点与已知平面垂直的直线方程，再求出所求的直线与已知平面的交点即可

  • 第18题：

    曲面xyz=1上平行于x+y+z+3=0的切平面方程是:

    A.x+y+z=0
    B.x+y+z=1
    C.x+y+z=2
    D.x+y+z=3

    答案：D
    解析：
    提示：利用两平面平行、法线向量平行、对应坐标成比例求M0坐标。

  • 第19题：

    已知曲面方程为x-yZ+z2-2x+8y+6z=10，则过点(5，-2.1)的切平面方程为( )。

    A、2x+3y+2z=0
    B、2x+y+2z=lO
    C、x-2y+6z=15
    D、x-2y+6z=0

    答案：B
    解析：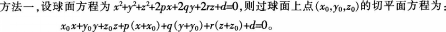

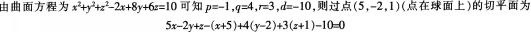
  • 第20题：

    单选题
    曲面x2/3＋y2/3＋z2/3＝4上任一点的切平面在坐标轴上的截距的平方和为（　　）。
    A

    32

    B

    48

    C

    64

    D

    16


    正确答案： A
    解析：
    构造函数F（x，y，z）＝x2/3＋y2/3＋z2/3－4，则Fx′＝2x－1/3/3，Fy′＝2y－1/3/3，Fz′＝2z－1/3/3。所以点M（x，y，z）处的切平面的方程为x－1/3（X－x）＋y－1/3（Y－y）＋z－1/3（Z－z）＝0。
    令X＝Y＝0，得Z＝4z1/3；令X＝Z＝0得Y＝4y1/3；令Y＝Z＝0，得X＝4x1/3。故X2＋Y2＋Z2＝（x2/3＋y2/3＋z2/3）·42＝64。

  • 第21题：

    填空题
    曲面x2＋2y2＋3z2＝21在点（1，－2，2）的法线方程为____。

    正确答案： (x-1)/1=(y+2)/(-4)=(z-2)/6
    解析：
    构造函数F（x，y，z）＝x2＋2y2＋3z2－21。则有Fx′（1，－2，2）＝2，Fy′（1，－2，2）＝－8，Fz′（1，－2，2）＝12，则所求法线的方向向量为（1，－4，6）。又法线过点（1，－2，2），故所求法线方程为（x－1）/1＝（y＋2）/（－4）＝（z－2）/6。

  • 第22题：

    填空题
    压力角是（）上径向直线与齿面在该点处的切平面所夹的锐角。

    正确答案： 分度圆
    解析： 暂无解析

  • 第23题：

    单选题
    曲面z=χ2+y2在(-1，2，5)处的切平面方程是（　）
    A

    2χ+4y+z=11

    B

    -2χ-4y+z=-1

    C

    2χ-4y-z=-15

    D

    2χ-4y+z=-5


    正确答案： B
    解析： 暂无解析

相关内容