问答题设AX(→)＝0(→)与BX(→)＝0(→)均为n元齐次线性方程组，秩r（A）＝r（B），且方程组AX(→)＝0(→)的解均为方程组BX(→)＝0(→)的解，证明方程组AX(→)＝0(→)与BX(→)＝0(→)同解。
题目
问答题
设AX(→)＝0(→)与BX(→)＝0(→)均为n元齐次线性方程组，秩r（A）＝r（B），且方程组AX(→)＝0(→)的解均为方程组BX(→)＝0(→)的解，证明方程组AX(→)＝0(→)与BX(→)＝0(→)同解。
相似考题
参考答案和解析
正确答案：
设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r。
构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r。
由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解。
设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r。
构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r。
由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解。
解析：
暂无解析
更多“设AX(→)＝0(→)与BX(→)＝0(→)均为n元齐次线性方程组，秩r（A）＝r（B），且方程组AX(→)＝0(→)的”相关问题
-
第1题：
设有方程组AX=O与BX=0,其中A,B都是m×N阶矩阵,下列四个命题：
(1)若AX=O的解都是BX=O的解,则r(A)≥r(B)
(2)若r(A)≥r(B),则AX=0的解都是BX=0的解
(3)若AX=0与BX=0同解,则r(A)-r(B)
(4)若r(A)=r（B）,则AX=0与BX=0同解
以上命题正确的是().A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(3)(4)答案：B解析：若方程组AX=0的解都是方程组BX=0的解，则n-r(A)≤n-r(B)，从而 r(A)≥r(B)，(1)为正确的命题；显然(2)不正确；因为同解方程组系数矩阵的秩相等，但
反之不对，所以(3)是正确的，(4)是错误的，选(B). -
第2题：
设有齐次线性方程组Ax=0和Bx=0, 其中A,B均为
矩阵，现有4个命题：① 若Ax=0的解均是Bx=0的解，则秩(A)
秩(B)；② 若秩(A)
秩(B)，则Ax=0的解均是Bx=0的解；③ 若Ax=0与Bx=0同解，则秩(A)=秩(B)；④ 若秩(A)=秩(B)， 则Ax=0与Bx=0同解，以上命题中正确的是A.① ②
B.① ③
C.② ④
D.③ ④答案：B解析：
-
第3题：
非齐次线性方程组Ax=b中未知量个数为n，方程个数为m，系数矩阵A的秩为r，则A.r=m时，方程组A-6有解.
B.r=n时，方程组Ax=b有唯一解.
C.m=n时，方程组Ax=b有唯一解.
D.r答案：A解析：因为A是m×n矩阵，若秩r(A)=m，则m=r(A)≤r(A，b)≤m.于是r(A)=r(A，b).故方程组有解，即应选(A).或，由r(A)=m，知A的行向量组线性无关，那么其延伸必线性无关，故增广矩阵(A，b)的m个行向量也是线性无关的，亦知r(A)=r(A，b).关于(B)、(D)不正确的原因是：由r(A)=n不能推导出r(A，b)=n(注意A是m×n矩阵，m可能大于n)，由r(A)=r亦不能推导出r(A，b)=r，你能否各举一个简单的例子？至于(C)，由克拉默法则，r(A)=n时才有唯一解，而现在的条件是r(A)=r，因此(C)不正确，第4题：
设有齐次线性方程组Ax=0和Bx=0，其中A，B均m×n矩阵，现有4个命题：
①若Ax=0的解均是Bx=0的解，则秩(A)≥秩(B)；
②若秩(A)≥秩(B)，则Ax=0的解均是Bx=0的解；
③若Ax=0与Bx=0同解，则秩(A)=秩(B)；
④若秩(A)=秩(B)则Ax=0与Bx=0同解；
以上命题中正确的是A.①②.
B.①③.
C.②④.
D.③④，答案：B解析：显然命题④错误，因此排除(C)、(D).对于(A)与(B)其中必有一个正确，因此命题①必正确，那么②与③哪一个命题正确呢？由命题①，“若Ax=0的解均是Bx=0的解，则秩(A)≥秩(B)”正确，知“若Bx=0的解均是Ax=0的解，则秩(B)≥秩(A)”正确，可见“若Ax=0与Bx=0同解，则秩(A)=秩(B)”正确.即命题③正确，故应选(B).第5题：
非齐线性方程组AX=b中未知量的个数为n，方程的个数为m，系数矩阵A的秩为r，则( )。A 当r=m时，方程组AX=b有解
B 当r=n时，方程组AX=b有惟一解
C 当m=n时，方程组AX=b有惟一解
D 当r＜n时，方程组AX=b有无穷多解答案：A解析：系数矩阵A是m×n矩阵，增个矩阵B是m×(n+1)矩阵当R(A)=r=m时，由于R(B)≥R(A)=m，而B仅有m行，故有R(B)≤m，从而R(B)=m，即R(A)=R(B)，方程组有解第6题：
设A是m×n阶矩阵,且非齐次线性方程组AX=b满足r(A)=r(A)=r答案：解析：
第7题：
非齐次线性方程组AX=b中未知数个数为n，方程个数为m，系数矩阵A的秩为r，则（ ）.A.r=m时，方程组AX=b有解
B.r=n时，方程组AX=b有唯一解
C.m=m时，方程组AX=b有唯一解
D.r＜n时，方程组AX=b有无穷多解答案：A解析：
第8题：
问答题设AX=0与BX=0均为n元齐次线性方程组，秩r（A）=r（B），且方程组AX=0的解均为方程组BX=0的解，证明方程组AX=0与BX=0同解.正确答案：
设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r.
构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r.
由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解.解析： 暂无解析第9题：
单选题设A为n阶方阵，则n元齐次线性方程组AX(→)＝0(→)仅有零解的充要条件是|A|（ ）。A＝0
B≠0
C＝1
D≠1
正确答案： B解析：
依据齐次线性方程组性质可知，系数行列式|A|≠0时，方程组仅有零解。第10题：
单选题设矩阵Am×n的秩r（A）=mAA的任意m个列向量必线性无关
BA的任一个m阶子式不等于0
C非齐次线性方程组AX=b一定有无穷多组解
DA通过行初等变换可化为（Em，0）
正确答案： A解析：
A项和B项，因r（A）=m，则A有m个列向量线性无关或A有m阶子式不为0，但不是任意的；C项，由r（A）=m<n，知方程组AX=b中有n-m个自由未知数，故其有无穷多解；D项，矩阵A仅仅通过初等行变换是不能变换为矩阵（Em，0）的．第11题：
填空题设n阶矩阵A的各行元素之和均为零，且A的秩为n－1，则线性方程组AX(→)＝0(→)的通解为____。正确答案： X=k(1,1,…,1)T解析：
由r（A）＝n－1，知方程组AX＝0的基础解系只含有n－（n－1）＝1个解向量。又矩阵A的各行元素之和为0，知（1，1，…，1）T，为AX＝0的非零解，则方程组AX＝0的通解为X＝k（1，1，…，1）T。第12题：
设A,B都是N阶矩阵,且存在可逆矩阵P,使得AP=B,则().A.A,B合同
B.A,B相似
C.方程组AX=0与BX=0同解
D.r(A)=r(B)答案：D解析：因为P可逆，所以r(A)=r(B)，选(D).第13题：
设有齐次线性方程组Ax=0和Bx=0, 其中A,B均为 矩阵，现有4个命题： ① 若Ax=0的解均是Bx=0的解，则秩(A) 秩(B)； ② 若秩(A) 秩(B)，则Ax=0的解均是Bx=0的解； ③ 若Ax=0与Bx=0同解，则秩(A)=秩(B)； ④ 若秩(A)=秩(B)， 则Ax=0与Bx=0同解
A.① ②
B.① ③
C.② ④
D.③ ④
答案：B解析：
第14题：
设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。A.若Ax=0仅有零解，则Ax=b有惟一解
B.若Ax=0有非零解，则Ax=b有无穷多个解
C.若Ax=b有无穷多个解，则Ax=0仅有零解
D.若Ax=b有无穷多个解，则Ax=0有非零解答案：D解析：
第15题：
设n元齐次线性方程组Ax=0的系数矩阵A的秩为r，则Ax=0有非零解的充要条件为（ ）。A.r=n
B.r＜n
C.r≥n
D.r＞n答案：B解析：Ax=0有非零解的充要条件为｜A｜=0，即矩阵A不是满秩的，r＜n。第16题：
设A为n阶矩阵,A的各行元素之和为0且r(A)=n-1,则方程组AX=0的通解为_______.答案：解析：
第17题：
设A为矩阵，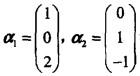
都是齐次线性方程组Ax=0的解，则矩阵A为( )。
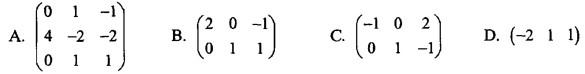答案：D解析：提示：由于
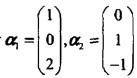线性无关，故R(A)= 1，显然选项A中矩阵秩为3,选项B和C中矩阵秩都为2。第18题：
设有齐次线性方程组Ax=0及Bx=0，其中A、B均为m×n矩阵，现有以下4个命题 ①若Ax=0的解均是Bx=0的解，则rA≥rB； ②若rA≥rB，则Ax=0的解均是Bx=0的解； ③若Ax=0与Bx=0同解，则rA=rB； ④若rA=rB，则Ax=0与Bx=0同解。 以上命题中正确的是（）。
- A、①②
- B、①③
- C、②④
- D、③④
正确答案:B第19题：
填空题设A为n阶方阵，则n元齐次线性方程组AX(→)＝0(→)仅有零解的充要条件是|A|____。正确答案： ≠0解析：
依据齐次线性方程组性质可知，系数行列式|A|≠0时，方程组仅有零解。第20题：
单选题设A为n阶方阵，则n元齐次线性方程组AX(→)＝0(→)仅有零解的充要条件是|A|（ ）。A＜0
B≠0
C＞0
D＝0
正确答案： A解析：
依据齐次线性方程组性质可知，系数行列式|A|≠0时，方程组仅有零解。第21题：
单选题设有齐次线性方程组Ax=0及Bx=0，其中A、B均为m×n矩阵，现有以下4个命题 ①若Ax=0的解均是Bx=0的解，则rA≥rB； ②若rA≥rB，则Ax=0的解均是Bx=0的解； ③若Ax=0与Bx=0同解，则rA=rB； ④若rA=rB，则Ax=0与Bx=0同解。 以上命题中正确的是（）。A①②
B①③
C②④
D③④
正确答案： B解析： 因为①中条件保证了n-r（A）≤n-r（B），所以r（A）≥r（B），而进一步易知③正确，而②、④均不能成立。