填空题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是____。
题目
填空题
已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是____。
相似考题
更多“已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1”相关问题
-
第1题：
设α1，α2是非齐次线性方程组Ax=b的解.则A（5α2-4α1）=_________.
正确答案：
b -
第2题：
设有方程组AX=O与BX=0,其中A,B都是m×N阶矩阵,下列四个命题：
(1)若AX=O的解都是BX=O的解,则r(A)≥r(B)
(2)若r(A)≥r(B),则AX=0的解都是BX=0的解
(3)若AX=0与BX=0同解,则r(A)-r(B)
(4)若r(A)=r（B）,则AX=0与BX=0同解
以上命题正确的是().A.(1)(2)
B.(1)(3)
C.(2)(4)
D.(3)(4)答案：B解析：若方程组AX=0的解都是方程组BX=0的解，则n-r(A)≤n-r(B)，从而 r(A)≥r(B)，(1)为正确的命题；显然(2)不正确；因为同解方程组系数矩阵的秩相等，但
反之不对，所以(3)是正确的，(4)是错误的，选(B). -
第3题：
非齐次线性方程组Ax=b中未知量个数为n，方程个数为m，系数矩阵A的秩为r，则A.r=m时，方程组A-6有解.
B.r=n时，方程组Ax=b有唯一解.
C.m=n时，方程组Ax=b有唯一解.
D.r答案：A解析：因为A是m×n矩阵，若秩r(A)=m，则m=r(A)≤r(A，b)≤m.于是r(A)=r(A，b).故方程组有解，即应选(A).或，由r(A)=m，知A的行向量组线性无关，那么其延伸必线性无关，故增广矩阵(A，b)的m个行向量也是线性无关的，亦知r(A)=r(A，b).关于(B)、(D)不正确的原因是：由r(A)=n不能推导出r(A，b)=n(注意A是m×n矩阵，m可能大于n)，由r(A)=r亦不能推导出r(A，b)=r，你能否各举一个简单的例子？至于(C)，由克拉默法则，r(A)=n时才有唯一解，而现在的条件是r(A)=r，因此(C)不正确，第4题：
已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3，且η1，η2，η3是3个不同的解向量，则通解是( ).A.x=k1(η-η2)+η3
B.x=k1η1+k2η2+η3
C.x=k1η1+k2η2+k3η3
D.x=k1(η+η2)+η3答案：A解析：由n=4，r=3得s=1。ηη2是 Ax=0的基础解系第5题：
设3阶实对称矩阵A的各行元素之和都为3,向量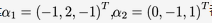
都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵
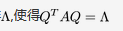答案：解析：
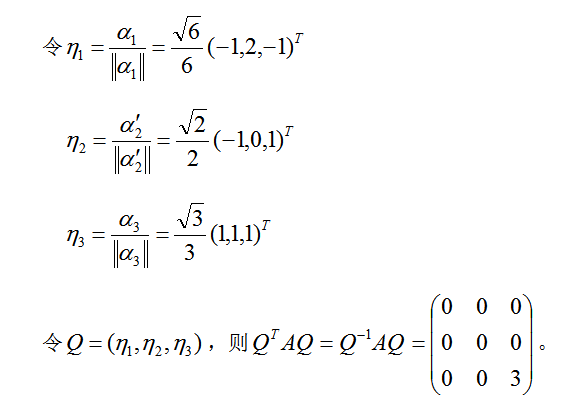
第6题：
设A是m×n阶矩阵,且非齐次线性方程组AX=b满足r(A)=r(A)=r答案：解析：
第7题：
已知齐次线性方程组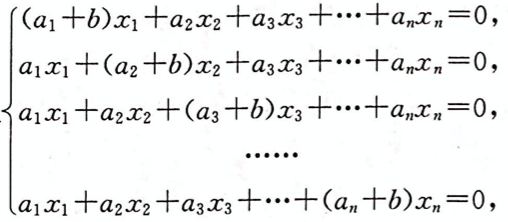
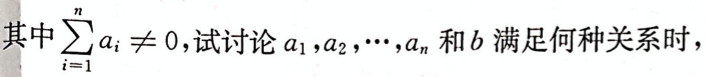（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.答案：解析：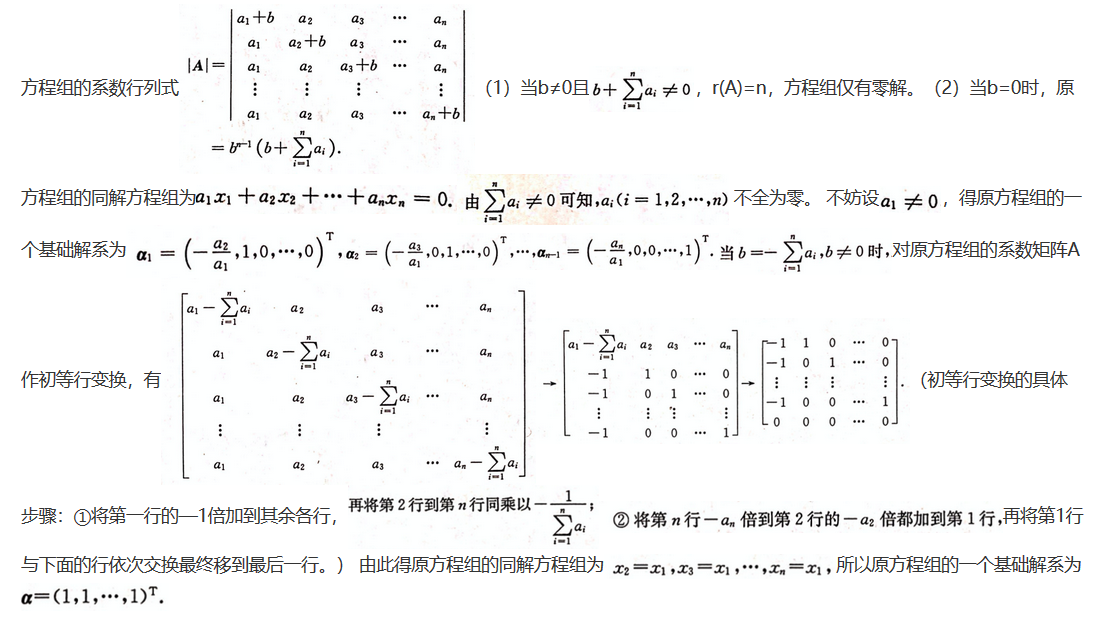
第8题：
非齐次线性方程组AX=b中未知数个数为n，方程个数为m，系数矩阵A的秩为r，则（ ）.A.r=m时，方程组AX=b有解
B.r=n时，方程组AX=b有唯一解
C.m=m时，方程组AX=b有唯一解
D.r＜n时，方程组AX=b有无穷多解答案：A解析：
第9题：
填空题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是____。正确答案： k(0,1,-1,-1)T+(1,1,0,2)T/2解析：
由Aα1＝b，Aα2＝b，故A[（α1＋α2）/2]＝b，则（α1＋α2）/2是方程组AX＝b的特解。又r（A）＝3，故四元齐次方程组AX＝b的基础解系只含有一个解向量。由α1，α3是AX＝b的解向量，知α1－α3是齐次方程组AX＝0的解，而α1－α3＝（α1＋α2）－（α2＋α3）＝（0，1，－1，－1）T，故AX＝b的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。第10题：
问答题设AX=0与BX=0均为n元齐次线性方程组，秩r（A）=r（B），且方程组AX=0的解均为方程组BX=0的解，证明方程组AX=0与BX=0同解.正确答案：
设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r.
构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r.
由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解.解析： 暂无解析第11题：
单选题设A为3阶方阵，α(→)1，α(→)2，α(→)3是互不相同的3维列向量，且都不是方程组Ax(→)＝0(→)的解，若B＝（α(→)1，α(→)2，α(→)3）满足r（AB）＜r（A），r（AB）＜r（B），则r（AB）等于（ ）。A3
B2
C1
D0
正确答案： C解析：
由于α1，α2，α3不是Ax＝0的解，故AB≠0，所以r（AB）＞0。
又因r（AB）＜r（A），故B不可逆，即r（B）≤2，从而r（AB）＜r（B）≤2，即r（AB）＝1。第12题：
单选题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是（ ）。Ak（0，1，－1，－1）T＋（1，1，0，2）T
Bk（0，1，－1，－1）T＋（1，1，0，2）T/2
Ck（1，1，0，2）T＋（0，1，－1，－1）T
Dk（1，1，0，2）T＋（0，1，－1，－1）T/2
正确答案： D解析：
由Aα1＝b，Aα2＝b，故A[（α1＋α2）/2]＝b，则（α1＋α2）/2是方程组AX＝b的特解。
又r（A）＝3，故四元齐次方程组AX＝b的基础解系只含有一个解向量。由α1，α3是AX＝b的解向量，知α1－α3是齐次方程组AX＝0的解，而α1－α3＝（α1＋α2）－（α2＋α3）＝（0，1，－1，－1）T，故AX＝b的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。第13题：
对于有5个变量的齐次线性方程组AX=0,系数矩阵的秩r(A)=3,则其基础解析中向量个数为()。A.2
B.5
C.3
D.1
正确答案：A
第14题：
若A是m×n矩阵，且m≠n，则当R（A）=n时，非齐次线性方程组AX=b，有唯一解答案：错解析：第15题：
设n阶矩阵A的伴随矩阵A^*≠0，若ζ1，ζ2，ζ3，ζ4是非齐次线性方程组Ax=b的互不相等的解，则对应的齐次线性方程组Ax=0的基础解系A.不存在.
B.仅含一个非零解向量.
C.含有两个线性无关的解向量.
D.含有三个线性无关的解向量.答案：B解析：
第16题：
设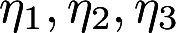
为3个n维向量,已知n元齐次方程组AX=0的每个解都可以用
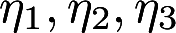线性表示,并且r(A)=n-3,证明{图2为AX=0的一个基础解系.}答案：解析：
第17题：
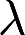取何值时,非齐次线性方程组
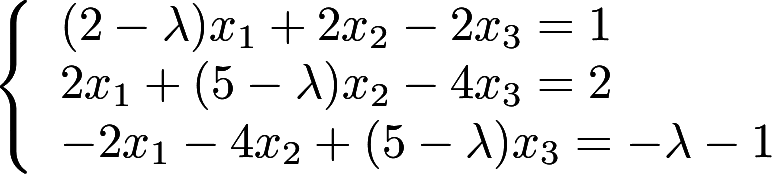(1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时，求方程组的通解。答案：解析：
第18题：
设3阶矩阵A=［α1，α2，α3］有3个不同的特征值，且a3=a1+2a2.
(Ⅰ)证明r(A)=2；
(Ⅱ)若β=α1，α2，α3，求方程组Ax=β的通解.答案：解析：
第19题：
已知al,a2，a3，a4是四维非零列向量，记A=(a1，a2,a3，a4)，A+是A的伴随矩阵，若齐次方程组AX=0的基础解系为(1，0,-2，0)T，则AX=0的基础解系为( )。A、al a2
B、a1 a3
C、al a2 a3
D、a2 a3 a4答案：D解析：AX=0的基础解系只含有一个向量，所以矩阵A的秩为3，所以A存在不为0的3阶子
即a1-2a3=0，所以a1与a3线性相关。而方程组的基本解系必须是线性相关的向量，所以正确答案为D。 第20题：
问答题设η(→)1，η(→)2，η(→)3，η(→)4是五元非齐次线性方程组AX(→)＝b(→)的四个解，且秩r（A）＝3，又设：η(→)1＋η(→)2＋η(→)3＋η(→)4＝（4，－8，－12，12，16）T，η(→)1＋2η(→)2＋2η(→)3＋η(→)4＝（6，18，－18，－30，12）T，2η(→)1＋2η(→)2＋η(→)3＋η(→)4＝（18，－30，－36，30，36）T，求方程组AX(→)＝b(→)的通解。正确答案：
由系数矩阵A的秩r(A)=3,知五元线性方程组的基础解系应含两个解向量。
由线性方程组解的性质知η2-η1,η3-η4,η1-η3,η2-η4都是其导出组的解,且它们的组合也是导出组的解,所以有
ξ1=(η2-η1)+(η3-η4)=2(η1+2η2+2η3+η4)-3(η1+η2+η3+η4)=(0,60,0,-96,-24)T
ξ2=(η1-η3)+(η2-η4)=2(2η1+2η2+η3+η4)-3(η1+η2+η3+η4)=(24,-36,-36,24,24)T
ξ1,ξ2是导出组的两个线性无关的解向量。又有
A[(η1+η2+η3+η4)/4]=(Aη1+Aη2+Aη3+Aη4)/4=(1/4)·4b=b所以η*=(η1+η2+η3+η4)/4=(1,-2,-3,3,4)T是AX=b的特解。故AX=b的通解为η=η*+k1ξ1+k2ξ2,k1,k2为任意常数。解析： 暂无解析第21题：
单选题设α(→)1，α(→)2，α(→)3，α(→)4是4维非零列向量组，A＝（α(→)1，α(→)2，α(→)3，α(→)4），A*是A的伴随矩阵，已知方程组AX(→)＝0(→)的基础解系为k（1，0，2，0）T，则方程组A*X(→)＝0(→)的基础解系为（ ）。Aα1，α2，α3
Bα1＋α2，α2＋α3，3α3
Cα2，α3，α4
Dα1＋α2，α2＋α3，α3＋α4，α4＋α1
正确答案： A解析：
由AX＝0的基础解系仅含有一个解向量，知r（A）＝4－1＝3，所以r（A*）＝1，则A*X＝0的基础解系含三个解向量。
又（α1，α2，α3，α4）（1，0，2，0）T＝0，即α1＋2α3＝0，知（α1，α3）线性相关，所以方程组A*X＝0的基础解系为α2，α3，α4。第22题：
单选题已知四元非齐次方程组AX(→)＝b(→)，r（A）＝3，α(→)1，α(→)2，α(→)3是它的三个解向量，且α(→)1＋α(→)2＝（1，1，0，2）T，α(→)2＋α(→)3＝（l，0，1，3）T，则AX(→)＝b(→)的通解是（ ）。Ak（0，1，1，1）T＋（1，1，0，2）T/2
Bk（0，1，－1，－1）T＋（1，1，0，2）T/2
Ck（0，1，1，－1）T＋（1，1，0，2）T/2
Dk（0，1，－1，1）T＋（1，1，0，2）T/2
正确答案： C解析：
由Aα1＝b，Aα2＝b，故A[（α1＋α2）/2]＝b，则（α1＋α2）/2是方程组AX＝b的特解。又r（A）＝3，故四元齐次方程组AX＝b的基础解系只含有一个解向量。由α1，α3是AX＝b的解向量，知α1－α3是齐次方程组AX＝0的解，而α1－α3＝（α1＋α2）－（α2＋α3）＝（0，1，－1，－1）T，故AX＝b的通解为k（0，1，－1，－1）T＋（1，1，0，2）T/2。第23题：
单选题已知n元非齐次线性方程组Ax＝B，秩r（A）＝n－2，α1，α2，α3为其线性无关的解向量，k1，k2为任意常数，则Ax＝B的通解为（ ）。[2014年真题]Ax＝k1（α1－α2）＋k2（α1＋α3）＋α1
Bx＝k1（α1－α3）＋k2（α2＋α3）＋α1
Cx＝k1（α2－α1）＋k2（α2－α3）＋α1
Dx＝k1（α2－α3）＋k2（α1＋α2）＋α1
正确答案： D解析：
n元非齐次线性方程组Ax＝B的通解为Ax＝0的通解加上Ax＝B的一个特解。因为r（A）＝n－2，Ax＝0的解由两个线性无关的向量组成，所以α2－α1，α2－α3是Ax＝0的两个线性无关解。所以Ax＝B的通解为：x＝k1（α2－α1）＋k2（α2－α3）＋α1。第24题：
单选题设n元齐次线性方程组AX(→)＝0(→)，秩（A）＝n－3，且α(→)1，α(→)2，α(→)3为其3个线性无关的解，则（ ）为其基础解系。Aα1＋α2，α2＋α3，α1＋α3
Bα1－α2，α2－α3，α3－α1
Cα1＋α2＋α3，α3－α2，α1＋2α3
Dα1－α2，2α2－3α3，3α3－2α1
正确答案： C解析：
B项，因（α1－α2）＋（α2－α3）＋（α3－α1）＝0，故其线性相关，不能构成AX＝0的基础解系。同理由（α1＋α2＋α3）＋（α3－α2）－（α1＋2α3）＝0，2（α1－α2）＋（2α2－3α3）＋（3α3－2α1）＝0知C、D项的向量组都线性相关。