单选题设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．A 2B 1/2C 1/3D 1/4

题目
单选题
设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．
A

2

B

1/2

C

1/3

D

1/4

相似考题

1.A.点(0，0)不是f(x，y)的极值点 B.点(0，0)是f(x，y)的极大值点 C.点(0，0)是f(x，y)的极小值点 D.根据所给条件无法判断点(0，0)是否为f(x，y)的极值点

2.的值为( )，其中L是抛物线y2=x 上从点A(1,-1)N点B(1,1)之间的一段弧。

3.设L是抛物线y=x2上从点A（1，1）到点O（0，0）的有向弧线，则对坐标的曲线积分等于（　　）。A、 0 B、 1 C、 -1 D、 2

4.已知函数f(x,y)在点(0,0)的某个邻域内连续，且 ，则A.点(0,0)不是f(x,y)的极值 B.点(0,0)是f(x,y)的极大值点 C.点(0,0)是f(x,y)的极小值点 D.根据所给条件无法判断点(0,0)是否为f(x,y)的极值点

更多“设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．”相关问题

  • 第1题：

    设L是连接点A（1，0）及点B（0，1）的直线段，则对弧长的曲线积分∫L（y-x）ds等于：


    答案：D
    解析：


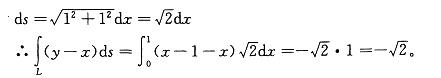
  • 第2题：

    曲线y=x3的拐点是( )。

    A、(0，0)
    B、x=0
    C、(1，1)
    D、y=0

    答案：A
    解析：
    由y'=3x2，y"=6x，当x=0，y"=0
    在(-∞，0)，y"＜0，曲线y=x3在(-∞，0)上向下凹
    在(0，+∞)，y"＞0，曲线y=x3在(0，+∞)上向上凹
    因此(0，0)为曲线y=x3的拐点

  • 第3题：

    已知函数f（x，y）在点（0，0）的某个邻域内连续，且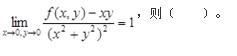

    A．点（0，0）不是f（x，y）的极值点
    B．点（0，0）是f（x，y）的极大值点
    C．点（0，0）是f（x，y）的极小值点
    D．根据所给条件无法判断点（0，0）是否为f（x，y）的极值点

    答案：A
    解析：
    由题设，容易推知f（0，0）=0，因此点（0，0）是否为f（x，y）的极值，关键看在点（0，0）的充分小的邻域内f（x，y）是恒大于零、恒小于零还是变号。

  • 第4题：

    设L是从点(0,0)沿:y=1- x-1 至点(2,0)的折线段，则曲线积分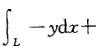xdy等于：
    A. 0 B. -1 C. 2 D. -2


    答案：D
    解析：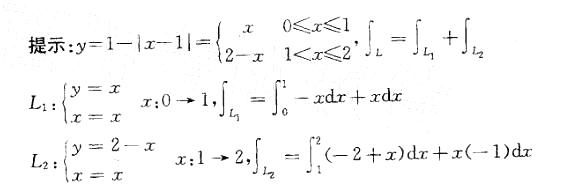

  • 第5题：

    已知曲线L的方程为y=1-｜x｜(x∈［-1，1］)，起点是(-1，0)，终点为(1，0)，则曲线积分________.


    答案：1、0.
    解析：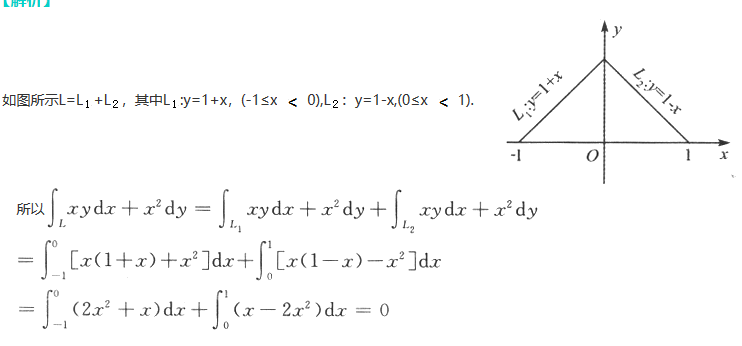

  • 第6题：

    设直线y=2x+m与抛物线y2=4x没有公共点，则m的取值范围是。


    答案：
    解析：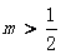

  • 第7题：

    设L为从点A（0，-2）到点B（2，0）的有向直线段，则对坐标的曲线积分



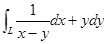
    等于（　　）。

    A.1
    B.-1
    C.3
    D.-3

    答案：B
    解析：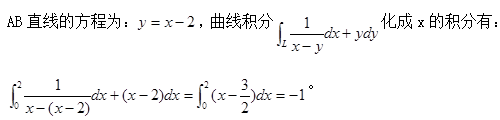


    @##

  • 第8题：

    设f（x）=|x（1-x）｜，则（ ）.《》（ ）

    A.x=0是f（x）的极值点，但（0，0）不是曲线y=f（x）的拐点
    B.x=0不是f（x）的极值点，但（0，0）是曲线y=f（x）的拐点
    C.x=0是f（x）的极值点，且（0，0）是曲线y=f（x）的拐点
    D.x=0不是f（x）的极值点，（0，0）也不是曲线y=f（x）的拐点

    答案：C
    解析：

  • 第9题：

    设抛物线y2=2px(p>0)焦点为F，点A坐标为(0，2)，若线段FA的中点B在抛物线上，则B到该抛物线准线距离为__________。


    答案：
    解析：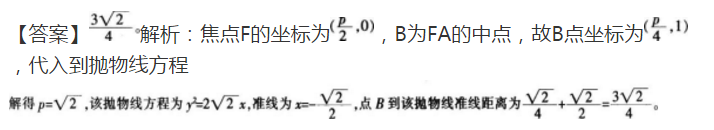

  • 第10题：

    设L是曲线y=lnx上从点（1，0）到点（e，1）的一段弧，则曲线积分=（）。

    • A、e
    • B、e-1
    • C、e+1
    • D、0

    正确答案:A

  • 第11题：

    单选题
    设L为抛物线y=x2上从0（0，0）到P（1，1）的一段弧，则曲线积分的值是（）．
    A

    1

    B

    0

    C

    1/2

    D

    -1


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    设L是曲线y=lnx上从点（1，0）到点（e，1）的一段弧，则曲线积分=（）。
    A

    e

    B

    e-1

    C

    e+1

    D

    0


    正确答案： A
    解析： 暂无解析

  • 第13题：

    设方程y´´-4y´+3y=0的某一积分曲线，它在点(0，2)处与直线x-y+2=0相切，则该积分曲线的方程是( ).

    A.
    B.
    C.
    D.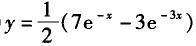

    答案：B
    解析：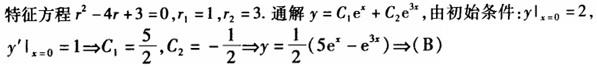

  • 第14题：

    设L为从点A（0，-2）到点B（2，0）的有向直线段，则对坐标的曲线积分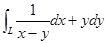

    等于（　　）。

    A、 1
    B、 -1
    C、 3
    D、 -3

    答案：D
    解析：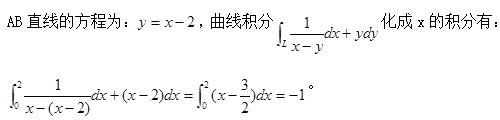

  • 第15题：

    设L为连接(0,0)点与(1,1)点的抛物线y =x2 ，则对弧长的曲线积分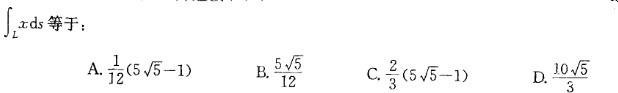


    答案：A
    解析：
    提示:利用对弧长的曲线积分方法计算。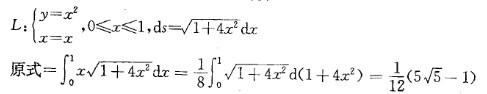

  • 第16题：

    计算曲线积分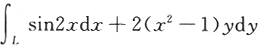，其中L是曲线y=sinx上从点(0，0)到点(π，0)的一段.


    答案：
    解析：
    【分析】利用曲线的参数方程直接转化为定积分计算或添加线段使之形成封闭曲线，再用格林公式，而添加线段上用参数法.

  • 第17题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第18题：

    设曲线y=y（x）过（0，0）点，M是曲线上任意一点，MP是法线段，P点在x轴上，已知MP的中点在抛物线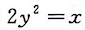，求此曲线的方程。


    答案：
    解析：

  • 第19题：

    设L是曲线y=lnx上从点(1，0)到点(e，1)的一段弧，则曲线积分（）。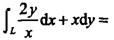
    A. e B. e-1 C. e+1 D. 0


    答案：A
    解析：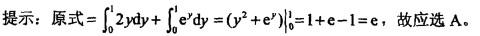

  • 第20题：

    已知P为抛物线y2=x的焦点，点M，N在该抛物线上且位于x轴的两侧，

    (其中O为坐标原点)，则ΔMPO与ΔNPO面积之和的最小值是( )。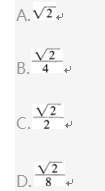


    答案：B
    解析：
    设直线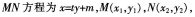

    直线方程与抛物线方程联立，可得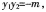


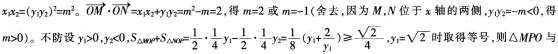
    △NPO面积之和的最小值是

  • 第21题：

    设函数f（x，y）＝x3+y3-3xy，则（）。

    • A、f（0，0）为极大值
    • B、f（0，0）为极小值
    • C、f（1，1）为极大值
    • D、f（1，1）为极小值

    正确答案:D

  • 第22题：

    设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．

    • A、2
    • B、1/2
    • C、1/3
    • D、1/4

    正确答案:C

  • 第23题：

    单选题
    使用Line控件在窗体上画一条从（0，0）到（600，700）的直线，则其相应属性的值应是（　　）。
    A

    X1＝0，X2＝600，Y1＝0，Y2＝700

    B

    Y1＝0，Y2＝600，X1＝0，X2＝700

    C

    X1＝0，X2＝0，Y1＝600，Y2＝700

    D

    Y1＝0，Y2＝0，X1＝600，X2＝700


    正确答案： A
    解析：
    X1，Y1，X2，Y2属性是直线的起点、终点坐标。

相关内容