设L是抛物线y=x2上从点A(1,1)到点O(0,0)的有向弧线,则对坐标的曲线积分等于( )。A、 0 B、 1 C、 -1 D、 2
题目
设L是抛物线y=x2上从点A(1,1)到点O(0,0)的有向弧线,则对坐标的曲线积分
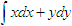
等于( )。
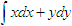
等于( )。
A、 0
B、 1
C、 -1
D、 2
B、 1
C、 -1
D、 2
相似考题
更多“设L是抛物线y=x2上从点A(1,1)到点O(0,0)的有向弧线,则对坐标的曲线积分 ”相关问题
-
第1题:
设方程y´´-4y´+3y=0的某一积分曲线,它在点(0,2)处与直线x-y+2=0相切,则该积分曲线的方程是( ).A.
B.
C.
D.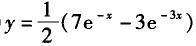 答案:B解析:
答案:B解析: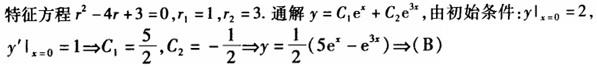
-
第2题:
曲线y=x3的拐点是( )。A、(0,0)
B、x=0
C、(1,1)
D、y=0答案:A解析:由y'=3x2,y"=6x,当x=0,y"=0
在(-∞,0),y"<0,曲线y=x3在(-∞,0)上向下凹
在(0,+∞),y">0,曲线y=x3在(0,+∞)上向上凹
因此(0,0)为曲线y=x3的拐点 -
第3题:
设L为连接(0,0)点与(1,1)点的抛物线y =x2 ,则对弧长的曲线积分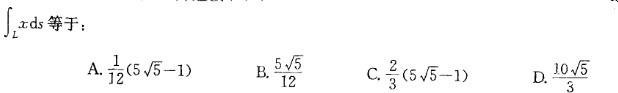 答案:A解析:提示:利用对弧长的曲线积分方法计算。
答案:A解析:提示:利用对弧长的曲线积分方法计算。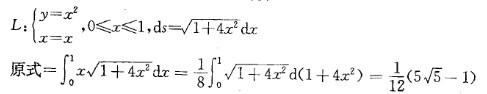
-
第4题:
曲线y=x3的拐点坐标是().A.(-1,-l)
B.(0,0)
C.(1,1)
D.(2.8)答案:B解析: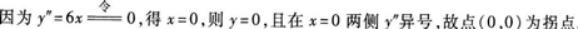
-
第5题:
设L是柱面x^2+y^2=1与平面z=x+y的交线,从z轴正向往z轴负向看去为逆时针方向,则曲线积分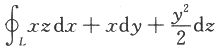 =________.答案:1、π.解析:用斯托克斯公式直接计算
=________.答案:1、π.解析:用斯托克斯公式直接计算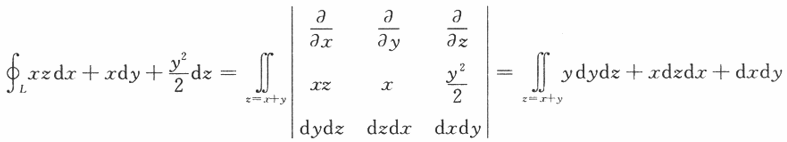
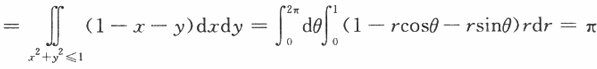
故应填π -
第6题:
设函数f(x)具有2阶连续导数,若曲线y=f(x)过点(0,0)且与曲线y=^x在点(1,2)处相切,则 =________.答案:1、2(ln2-1)解析:
=________.答案:1、2(ln2-1)解析:
-
第7题:
设曲线y=y(x)过(0,0)点,M是曲线上任意一点,MP是法线段,P点在x轴上,已知MP的中点在抛物线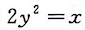 ,求此曲线的方程。答案:解析:
,求此曲线的方程。答案:解析:
-
第8题:
设L为从点A(0,-2)到点B(2,0)的有向直线段,则对坐标的曲线积分
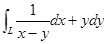
等于( )。A.1
B.-1
C.3
D.-3答案:B解析: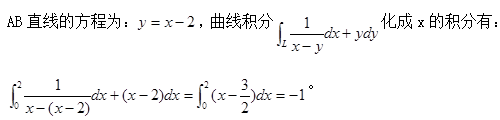
@## -
第9题:
设f(x)=|x(1-x)|,则( ).《》( )A.x=0是f(x)的极值点,但(0,0)不是曲线y=f(x)的拐点
B.x=0不是f(x)的极值点,但(0,0)是曲线y=f(x)的拐点
C.x=0是f(x)的极值点,且(0,0)是曲线y=f(x)的拐点
D.x=0不是f(x)的极值点,(0,0)也不是曲线y=f(x)的拐点答案:C解析: -
第10题:
设C为抛物线y2=x上从点0(0,0)到点P(1,1)的一段弧,则曲线积分的值是().
- A、2
- B、1/2
- C、1/3
- D、1/4
正确答案:C -
第11题:
单选题设抛物线x2=8y上任一点到点A(0,2)的距离为d1,到直线y=-2的距离为d2,则d1,d2的大小关系是( ).Ad1=d2
Bd1<d2
Cd1>d2
D无法确定
正确答案: B解析:
由题意可知,点A为此抛物线的焦点,y=-2为抛物线的准线,所以有d1=d2. -
第12题:
单选题设C为抛物线y2=x上从点0(0,0)到点P(1,1)的一段弧,则曲线积分的值是().A2
B1/2
C1/3
D1/4
正确答案: C解析: 暂无解析 -
第13题:
设圆周曲线L:x2+y2=1取逆时针方向,则对坐标的曲线积分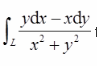
值等于( )。A.2π
B.-2π
C.π
D.0答案:B解析:采用三角函数代换法,令x=cosx,y=sinx。则: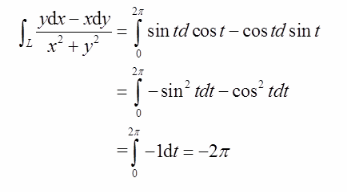
-
第14题:
设L为从点A(0,-2)到点B(2,0)的有向直线段,则对坐标的曲线积分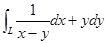
等于( )。A、 1
B、 -1
C、 3
D、 -3答案:D解析: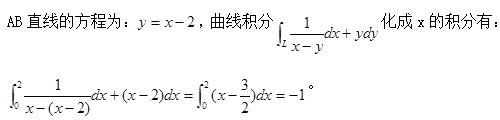
-
第15题:
设L是从点(0,0)沿:y=1- x-1 至点(2,0)的折线段,则曲线积分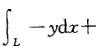 xdy等于:
xdy等于:
A. 0 B. -1 C. 2 D. -2答案:D解析: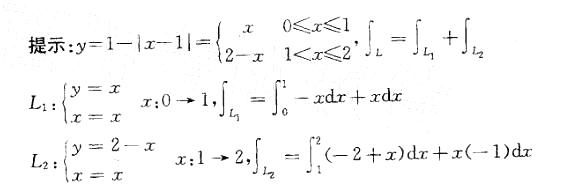
-
第16题:
计算曲线积分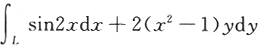 ,其中L是曲线y=sinx上从点(0,0)到点(π,0)的一段.答案:解析:【分析】利用曲线的参数方程直接转化为定积分计算或添加线段使之形成封闭曲线,再用格林公式,而添加线段上用参数法.
,其中L是曲线y=sinx上从点(0,0)到点(π,0)的一段.答案:解析:【分析】利用曲线的参数方程直接转化为定积分计算或添加线段使之形成封闭曲线,再用格林公式,而添加线段上用参数法.
-
第17题:
已知曲线L的方程为y=1-|x|(x∈[-1,1]),起点是(-1,0),终点为(1,0),则曲线积分________.答案:1、0.解析: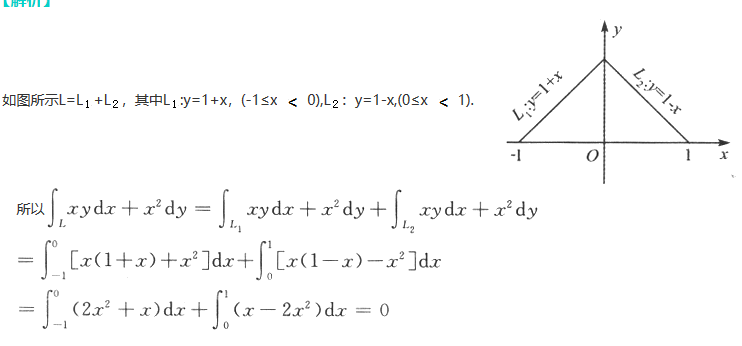
-
第18题:
抛物线x2=-16y上一点P到焦点的距离是6,则点P的坐标是( )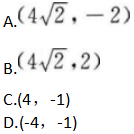 答案:A解析:【考情点拨】本题主要考查的知识点为抛物线的定义. 【应试指导】本题应从抛物线的定义去考虑.
答案:A解析:【考情点拨】本题主要考查的知识点为抛物线的定义. 【应试指导】本题应从抛物线的定义去考虑.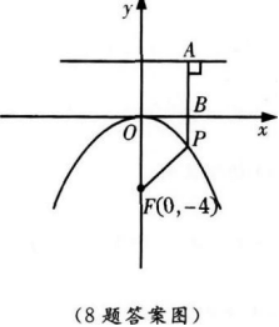

∴F(0,-4),
∴准线方程y=4,由题意得|PF|=6,
∴|PA|=6,
∵|AB|=4,
∴|PB|=2,
∴P点的坐标为(x,-2),
∵P(x,-2)点在抛物线上,
∴x2=-16×(-2)=32.
-
第19题:
设L是从A(1,0)到B(-1,2)的直线段,则曲线积分∫L(x+y)ds=( )。 答案:B解析:
答案:B解析: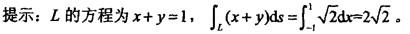
-
第20题:
设L是曲线y=lnx上从点(1,0)到点(e,1)的一段弧,则曲线积分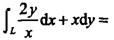 ()。
()。
A. e B. e-1 C. e+1 D. 0答案:A解析: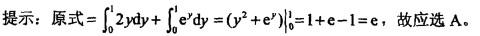
-
第21题:
设函数f(x,y)=x3+y3-3xy,则()。
- A、f(0,0)为极大值
- B、f(0,0)为极小值
- C、f(1,1)为极大值
- D、f(1,1)为极小值
正确答案:D -
第22题:
单选题设L为抛物线y=x2上从0(0,0)到P(1,1)的一段弧,则曲线积分的值是().A1
B0
C1/2
D-1
正确答案: A解析: 暂无解析 -
第23题:
单选题设L是曲线y=lnx上从点(1,0)到点(e,1)的一段弧,则曲线积分=()。Ae
Be-1
Ce+1
D0
正确答案: A解析: 暂无解析
