单选题度相同但格式不同的2种浮点数，假定前者阶段长、尾数短，后者阶段短、尾数长，其他规定均相同，则它们可表示的数的范围和精度为（）。A 两者可表示的数的范围和精度相同B 前者可表示的数的范围大但精度低C 后者可表示的数的范围大且精度高D 前者可表示的数的范围大且精度高

题目
单选题
度相同但格式不同的2种浮点数，假定前者阶段长、尾数短，后者阶段短、尾数长，其他规定均相同，则它们可表示的数的范围和精度为（）。
A

两者可表示的数的范围和精度相同

B

前者可表示的数的范围大但精度低

C

后者可表示的数的范围大且精度高

D

前者可表示的数的范围大且精度高

相似考题

1.浮点数的表示范围和精度取决于()A、阶码的位数和尾数的位数B、阶码采用的编码和尾数的位数C、阶码采用的编码和尾数采用的编码D、阶码的位数和尾数采用的编码

2.若浮点数用补码表示，则判断运算结果是否为规格化数的方法是A.阶符与数符相同B.阶符与数符相异C.数符与尾数小数点后第一位数字相异D.数符与尾数小数点后第一位数字相同

3.浮点数的一般表示形式为N=2E×F，其中E为阶码，F为尾数。以下关于浮点表示的叙述中，错误的是( )。两个浮点数进行相加运算，应首先( )。A．阶码的长度决定浮点表示的范围，尾数的长度决定浮点表示的精度B．工业标准IEEE754浮点数格式中阶码采用移码、尾数采用原码表示C．规格化指的是阶码采用移码、尾数采用补码D．规格化表示要求将尾数的绝对值限定在区间[O．5，1)

4.长度相同但格式不同的2种浮点数,前者尾数长、阶码短,后者尾数短、阶码长,其他规定均相同,则前者可表示的数的范围大但精度低。()此题为判断题(对，错)。

参考答案和解析
正确答案： A
解析： 暂无解析
更多“度相同但格式不同的2种浮点数，假定前者阶段长、尾数短，后者阶段短、尾数长，其他规定均相同，则它们可表示的数的范围和精度为”相关问题

  • 第1题：

    在相同的机器字长和尾数位数的情况下,浮点数尾数基值取小,可使浮点数( )。

    A.运算过程中数的精度损失降低

    B.数在数轴上的分布变密

    C.可表示数的范围增大

    D.可表示数的个数增多


    参考答案：B

  • 第2题：

    长度相同但格式不同的两个浮点数，假设前者阶码长，尾数短，后者相反，其他规定均相同，则它们可以表示的数的范围和精度是( )。

    A．两者可以表示的数的范围和精度相同

    B．前者可以表示的数的范围大但精度底

    C．后者可以表示的数的范围大且精度高

    D．前者可以表示的数的范围大且精度高


    正确答案：B

  • 第3题：

    长度相同但格式不同的两种浮点数，假设前者阶码长、尾数短；后者阶码短、尾数长，其他规定均相同，则它们可表示的数的范围和精度相比为( )。

    A．两者可表示的数的范围和精度相同

    B．前者可表示的数的范围大但精度低

    C．后者可表示的数的范围大且精度高

    D．前者可表示的数的范围大且精度高


    正确答案：B

  • 第4题：

    长度相同但格式不同的两种浮点数，假设前者阶码长、尾数短，后者阶码短、尾数长，其他规定均相同，则它们可以表示的数的范围和精度是______。

    A．两者可以表示的数的范围和精度相同

    B．前者可以表示的数的范围大但精度低

    C．后者可以表示的数的范围大但精度高

    D．前者可以表示的数的范围大但精度高


    正确答案：B
    解析：浮点数其实就是实数。一个实数可以表示成一个纯小数(尾数)和一个乘幂(指数)之积，其中指数部分用来指出实数中小数点的位置。任何一个实数，在计算机内部都可以用指数(整数形式)和尾数(小数形式)来表示。指数的位数多少决定了数值的范围，指数位数越多可表示的数的范围越大。尾数的位数决定了数的精度，尾数的位数越多可以表示的数的精度越高。

  • 第5题：

    有两种采用同时进制的长度相同但格式不同的浮点数，其中，前者的阶码短、尾数长，后者的阶码长、尾数短，则它们可表示的数的范围和精度的情况是(36)。

    A．前者可表示的数的范围较小、精度较低

    B．前者可表示的数的范围较大但精度较低

    C．后者可表示的数的范围较小、精度较低

    D．后者可表示的数的范围较大但精度较低


    正确答案：D
    解析：阶码越长表示的数的范围越大，尾数越长表示数的精度也越高。

  • 第6题：

    设16位浮点数，其中阶符1位、阶码值6位、数符1位、尾数8位。若阶码用移码表示，尾数用补码表示，则该浮点数所能表示的数值范围是（ ）。



    答案：B
    解析：

  • 第7题：

    字长相同的两种浮点数，第一种阶码位数多，尾数位数少，第二种阶码位数少，尾数位数多，阶的底数都是2，则有()。

    A.它们表示的数的范围与精度相同
    B.第一种数的范围大，但精度低
    C.第一种数的范围大，精度高
    D.第一种数的范围小，精度高

    答案：C
    解析：
    字长相同的两种浮点数，阶码位数较多表示的数范围越大，尾数越多表示的精度越高。

  • 第8题：

    在相同机器字长和尾数位数的情况下，浮点数尾数基值取小，可使浮点数()。

    A.可表示数的范围增大
    B.可表示数的个数增多
    C.运算过程中数的精度损失降低
    D.数在数轴上的分布变密

    答案：D
    解析：
    浮点数中尾数决定了数据的精度，尾数越小，指数相同，则两个数值越接近。

  • 第9题：

    设浮点数的格式为：阶码 5 位，尾数 6 位，均用补码表示，请计算 X+Y 和 X-Y。（阶码和尾数均用补码计算）。【＊＊，★，包捷 4.8，编号 2.3】 X=-1.625，Y=5.25


    正确答案:1）方法一：（双符号法）
    X.-1.625=-1.101B=-0.1101*21
    [X]浮=00，000111.00110
    Y.5.25=101.01B=0.10101*211
    [Y]浮=00，001100.10101
    计算X+Y：
    对阶
    [X]阶<[Y]阶，X向Y对齐。X尾数右移2位，X阶码+2
    [X]浮=00，001111.11001（10）
    尾数相加
    [X]尾+[Y]尾=11.11001（10）+00.10101=00.01110（10）（mod4）
    结果规格化：双符号00，无溢出。但有一个前导0，需要左规1位：尾数左移1位，阶码-1
    [X+Y]尾=00.11101（0）
    [X+Y]阶=00，0011-1=00，0011+（100，0000-1）=00，0011+11，1111=00，0010（无溢出）
    舍入
    [X+Y]浮=0，00100.11101//舍去0
    计算X-Y：
    对阶
    [X]阶<[Y]阶，X向Y对齐。X尾数右移2位，X阶码+2
    [X]浮=00，001111.11001（10）
    尾数相减
    [X]尾-[Y]尾=11.11001（10）+（100.00000-00.10101）=11.11001+11.01011=11.00100（10）
    结果规格化：双符号11，无溢出。结果已规格化
    舍入：入1
    [X-Y]浮=0，00111.00101

  • 第10题：

    度相同但格式不同的2种浮点数，假定前者阶段长、尾数短，后者阶段短、尾数长，其他规定均相同，则它们可表示的数的范围和精度为（）。

    • A、两者可表示的数的范围和精度相同
    • B、前者可表示的数的范围大但精度低
    • C、后者可表示的数的范围大且精度高
    • D、前者可表示的数的范围大且精度高

    正确答案:B

  • 第11题：

    单选题
    浮点数的表示范围和精度取决于（）
    A

    阶码的位数和尾数的位数

    B

    阶码采用的编码和尾数的位数

    C

    阶码采用的编码和尾数采用的编码

    D

    阶码的位数和尾数采用的编码


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    度相同但格式不同的2种浮点数，假定前者阶段长、尾数短，后者阶段短、尾数长，其他规定均相同，则它们可表示的数的范围和精度为（）。
    A

    两者可表示的数的范围和精度相同

    B

    前者可表示的数的范围大但精度低

    C

    后者可表示的数的范围大且精度高

    D

    前者可表示的数的范围大且精度高


    正确答案： C
    解析： 暂无解析

  • 第13题：

    长度相同但格式不同的2种浮点数，假定前者阶段长、尾数短，后者阶段短、尾数长，其他规定均相同,则它们可表示的数的范围和精度______。

    A.两者可表示的数的范围和精度相同

    B.前者可表示的数的范围大但精度低

    C.后者可表示的数的范围大且精度高

    D.前者可表示的数的范围大且精度高


    正确答案：B

  • 第14题：

    下面是机器中浮点数的表示格式：

    设浮点数的基为2。若阶码用补码表示、尾数用原码表示，十进制数-51.875采用上述格式可表示为(7)；若阶码用移码表示、尾数用补码表示，该数可表示为(8)。

    A．0110 111001111100

    B．0110 011001111100

    C．0110 001110011111

    D．0101 011001111100


    正确答案：A
    解析：首先将-51.875转换为二进制表示：(-51.875)10=-110011.111=-0.110011111×2110，其中110是阶码，-0.110011111是尾数(绝对值大于0.5)。由于规格化表示格式中阶符和阶码共计4位，本题中阶码大于0，故采用补码时，这4位应该是[110]补=[110]原=0110。而采用原码表示尾数时，向[-0.110011111]原=1110011111后面添零补足12位，得111001111100。

  • 第15题：

    若浮点数用补码表示，判断结果是否为规格化数的方法是(10)。

    A．阶符与数符相同

    B．阶符与数符相异

    C．数符与尾数最高有效位相异

    D．数符与尾数最高有效位相同


    正确答案：C
    解析：本题考查浮点数的规格化。规格化的浮点数形式分为尾数和阶码两部分。将数表示成规格化的浮点数形式时，需要事先规定尾数和阶码的位数及采用的编码方式，题目中说明是用补码表示，在用补码表示时，判定结果是否为规格化数的方法是判断数符与尾数最高有效位是否相同，如果相同，则不是规格化数；如果不同，则是规格化数。

  • 第16题：

    设32位浮点数格式如下。以下关于浮点数表示的叙述中，正确的是（ ）。若阶码采用补码表示，为8位（含1位阶符），尾数采用原码表示，为24位（含1位数符），不考虑规格化，阶码的最大值为（ ）。

    A.浮点数的精度取决于尾数M的位数，范围取决于阶码E的位数B.浮点数的精度取决于阶码E的位数，范围取决于尾数M的位数C.浮点数的精度和范围都取决于尾数M的位数，与阶码E的位数无关D.浮点数的精度和范围都取决于阶码E的位数，与尾数M的位数无关A.255 B.256 C.127 D.128


    正确答案：A,C

  • 第17题：

    长度相同但格式不同的两种浮点数，假设前者阶码长、尾数短、后者阶码短、尾数长，其他规定均相同，则它们可以表示的数的精度和范围是( )

    A．两者可以表示的数的精度和范围相同

    B．前者可以表示的数的范围大但精度低

    C．后者可以表示的数的范围大且精度高

    D．前者可表示的数的范围大且精度高


    正确答案：B
    解析：“浮点数”由两部分组成，即尾数和阶码。在浮点表示方法中，小数点的位置是浮动的，阶码可取不同的数值。为了便于计算机中小数点的表示，规定将浮点数写成规格化的形式，即尾数的绝对值大于等于0.1并且小于1，从而唯一规定了小数点的位置。尾数的长度将影响数的精度，其符号将决定数的符号。浮点数的阶码相当于数学中的指数，其大小将决定数的表示范围。一个浮点数在计算机中的表现形式如下：尾数符号阶码尾数有效值。当长度相同的两种浮点数，阶码长、尾数短的当然表示数的范围大，精度低。而尾数长、阶码短的表示数的范围小，精度高。所以选项B是正确的。

  • 第18题：

    若浮点数用原码表示，则判断运算结果为规格化数的方法是()。

    A.阶符与数符相同
    B.阶符与数符相异
    C.尾数最高数值位为1
    D.尾数符号与尾数最高数值位不相同

    答案：C
    解析：
    为了提高浮点数的精度，其尾数必须为规格化数，当基数为2时，尾数最高位为l的数为规格化数。题干中浮点数用原码表示与真值的二进制表示之间只是符号位表示上的不同。

  • 第19题：

    长度相同但格式不同的2种浮点数，假定前者阶码长、尾数短，后者阶码短、尾数长，其他规定均相同，则它们可表示的数的范围和精度为()。

    A.两者可表示的数的范围和精度相同
    B.前者可表示的数的范围大且精度高
    C.后者可表示的数的范围大且精度高
    D.前者可表示的数的范围大但精度低

    答案：D
    解析：
    在浮点数表示法中，阶码影响表示的范围，阶码越长表示的范围越大，尾数影响精度，尾数越长，表示的精度越高。

  • 第20题：

    某浮点数格式如下：7 位阶码（包含一个符号位），9 位尾数（包含一个符号位）。若阶码用移码、尾数用规格化的补码表示，则浮点数所能表示数的范围是（）。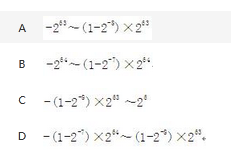


    答案：A
    解析：
    浮点数所能表示的数值范围如下：最大的正数

  • 第21题：

    若浮点数的阶码和尾数都用补码表示，则判断运算结果是否为规格化数的方法是（）。

    • A、阶符与数符相同为规格化数
    • B、阶符与数符相异为规格化数
    • C、数符与尾数小数点后第一位数字相异为规格化数
    • D、数符与尾数小数点后第一位数字相同为规格化数

    正确答案:C

  • 第22题：

    设浮点数的格式为：阶码 5 位，尾数 6 位，均用补码表示，请计算 X+Y 和 X-Y。（阶码和尾数均用补码计算）。【＊＊，★，包捷 4.8，编号 2.3】 X=15/64，Y=-25/256


    正确答案:方法一（双符号法）
    X.1111X2-6=0.1111X2-10
    [X]浮=11，111000.11110
    Y.-11101X2-8=-0.11101X2-11
    [Y]浮=11，110111.00011
    计算X+Y：
    1.对阶
    Y.向X对齐，Y的尾数右移1位。
    [Y]浮=11，111011.10001（1）
    2.尾数相加
    [X]尾+[Y]尾=00.11110+11.10001（1）=00.01111（1）
    3.结果规格化：双符号00，无溢出。一个前导0，左规一位。
    [Z]尾=00.11111
    [Z]阶=11，1110-1=11，1101
    4. 舍入：
    [X+Y]浮=1,1101 0.11111
    计算 X-Y：
    5. 对阶
    Y 向 X 对齐，Y 的尾数右移 1 位。
    [Y]浮=11,1110 11.10001(1)
    6. 尾数相减
    [X]尾-[Y]尾=00.11110-11.10001(1)=00.11110+(100.00000-11.10001(1))=01.01100(1)
    7. 结果规格化：双符号 01，有溢出。右规一位，阶码+1
    [X-Y]尾=00.10110(01)
    [X-Y]阶=11,1110+1=11,1111
    8. 舍入
    [X-Y]浮=1,1111 0.10110

  • 第23题：

    单选题
    长度相同但格式不同的2种浮点数，假设前者阶码长、尾数短，后者阶码短、尾数长，其他规定均相同，则它们可表示的数的范围和精度为（）。
    A

    两者可表示的数的范围和精度相同

    B

    前者可表示的数的范围大但精度低

    C

    后者可表示的数的范围大且精度高

    D

    前者可表示的数的范围大且精度高


    正确答案： C
    解析： 暂无解析

  • 第24题：

    单选题
    在相同机器字长和尾数位数的情况下，浮点数尾数基值取小，可使浮点数(  )。
    A

    可表示数的范围增大

    B

    可表示数的个数增多

    C

    运算过程中数的精度损失降低

    D

    在数轴上的分布变密


    正确答案： B
    解析：

相关内容