问答题设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。

题目
问答题
设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。
相似考题

1.n阶对称矩阵A正定的充分必要条件是()。A、|A|0B、存在n阶方阵C使A=CTCC、负惯性指标为零D、各阶顺序主子式均为正数

2.若把A分解成一个下三角阵L和一个单位上三角阵U的乘积，称为克洛特(Crout)分解。()

3.将非奇异阵A分解成一个下三角阵L和一个上三角阵U的乘积：A=LU称为对矩阵A的三角分解。()

4.设A为m*n矩阵,则有()。A、若mn，则有ax=b无穷多解B、若mn，则有ax=0非零解，且基础解系含有n-m个线性无关解向量;C、若A有n阶子式不为零，则Ax=b有唯一解;D、若A有n阶子式不为零，则Ax=0仅有零解。

更多“设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。”相关问题

  • 第1题：

    设A为n阶实对称矩阵,下列结论不正确的是().

    A.矩阵A与单位矩阵E合同
    B.矩阵A的特征值都是实数
    C.存在可逆矩阵P,使P^-1AP为对角阵
    D.存在正交阵Q,使Q^TAQ为对角阵

    答案：A
    解析：
    根据实对称矩阵的性质，显然(B)、(C)、(D)都是正确的，但实对称矩阵不一定是正定矩阵，所以A不一定与单位矩阵合同，选(A).

  • 第2题：

    设A为n阶矩阵，则A以零为其特征值是A为奇异矩阵(即 A =0)的:
    A.充分非必要条件
    B.必要非充分条件
    C.既非充分也非必要条件
    D.充分必要条件


    答案：D
    解析：
    提示:可通过下面证明说明。充分性:若矩阵A有特征值0→矩阵A奇异(即 A =0)，若λ=0为矩阵A的特征值，则存在非零向量a，使Aa=0a，Aa=0，即齐次线性方程组Ax =0有非零解，故 A =0，故矩阵A为奇异矩阵。
    必要性:若矩阵A是奇异矩阵，即 A =0→λ=0是矩阵A的特征值，已知A是奇异矩阵， A =0，取λ=0，有 A-λE = A-0E= A =0，λ=0，满足特征方程 A-λE =0，故λ=0 是矩阵A的特征值。

  • 第3题：

    设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.


    答案：
    解析：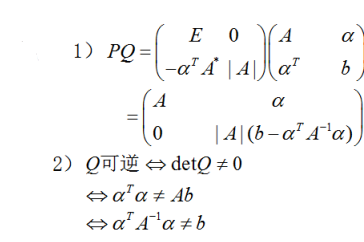

  • 第4题：

    设A为三阶方阵，A*为矩阵A的伴随矩阵，，请计算


    答案：
    解析：

  • 第5题：

    设A是m×n矩阵，秩（A）=r＜min（m，n），则A中必（ ）

    A.至少有-r阶子式不为零，没有不等于0的r+1阶子式
    B.有等于0的r阶子式，所有r+l阶子式全为0
    C.有等于0的r阶子式，没有不等于0的r+1阶子式
    D.有等于0的r-1阶子式，有不等于0的r阶子式

    答案：A
    解析：
    由矩阵A的秩（A）=r＜min（m，n），知所有r+1阶子式全为0，r阶子式至少有一个不为0.

  • 第6题：

    由高斯消去法说明当Δi≠0（i=1，2，...，n-1）时，则A=LU，其中L为单位下三角阵，U为上三角阵。


    正确答案: 高斯消去法第k步等价于左乘单位下三角矩阵Lk，而顺序主子式均不为零保证所得矩阵对角元不为零，可进行第k+1步消元，U=A（n）=Ln...L1A，A=L1-1...Ln-1U=LU。

  • 第7题：

    X为3阶随机矩阵，分别对X进行如下操作： 求X的三角分解；求X的正交分解；求X的特征值分解；求X的奇异值分解；


    正确答案: >>X=rand（3）
    >>[L，U]=lu（X）
    >>[Q，R]=qr（X）
    >>[V，D]=eig（X）
    >>[U，S，V]=svd（X）

  • 第8题：

    当满足（）条件时，矩阵A为负定矩阵。

    • A、各阶顺序主子式均大于零
    • B、各阶顺序主子式均小于零
    • C、所有参数阶主子式小于零
    • D、所有参数阶主子式大于零

    正确答案:C

  • 第9题：

    设A，B是n阶对称阵，Λ是对角阵，下列矩阵中不是对称阵的是（）．

    • A、A+2E
    • B、A+Λ
    • C、AB
    • D、A-B

    正确答案:C

  • 第10题：

    问答题
    设A是n阶矩阵，且满足Am＝E，其中m为整数，E为n阶单位矩阵。令将A中的元素aij换成它的代数余子式Aij而成的矩阵为A(～)，证明：（A(～)）m＝E。

    正确答案：
    因为Am=E,所以,Am,=,A,m=1,,A,=1≠0,即矩阵A可逆。
    由题知A(~)=(A*)T,其中A*为A的伴随矩阵。所以有(A(~))m=[(A*)T]m=[(,A,A-1)T]m=[(A-1)T]m=[(Am)-1]T=E。
    解析： 暂无解析

  • 第11题：

    填空题
    设A为4阶方阵，且r（A）＝3，A*为A的伴随矩阵，则r（A*）＝____。

    正确答案： 1
    解析：
    由A是4阶方阵且r（A）＝3，知|A|＝0，又AA*＝|A|E＝0为A的齐次方程组，则A*的列向量是齐次方程组Ax(→)＝0(→)的解，故r（A）＋r（A*）≤4，则r（A*）≤1。由r（A）＝3知，A至少有一个代数余子式不为0，故A*≠0，所以r（A*）＝1。

  • 第12题：

    单选题
    下列结论中正确的是（    ）
    A

    矩阵A的行秩与列秩可以不等

    B

    秩为r的矩阵中，所有r阶子式均不为零

    C

    若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零

    D

    秩为r的矩阵中，不存在等于零的r-1阶子式


    正确答案： D
    解析：

  • 第13题：

    下列结论中正确的是（　　）。

    A、 矩阵A的行秩与列秩可以不等
    B、 秩为r的矩阵中，所有r阶子式均不为零
    C、 若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零
    D、 秩为r的矩阵中，不存在等于零的r-1阶子式

    答案：C
    解析：
    A项，矩阵A的行秩与列秩一定相等。B项，由矩阵秩的定义可知，若矩阵A（m×n）中至少有一个r阶子式不等于零，且r＜min（m，n）时，A中所有的r+1阶子式全为零，则A的秩为r。即秩为r的矩阵中，至少有一个r阶子式不等于零，不必满足所有r阶子式均不为零。C项，矩阵A的行列式不等于零意味着矩阵A不满秩，n阶矩阵的秩为n时，所对应的行列式的值大于零；当n阶矩阵的秩＜n时，所对应的行列式的值等于零。D项，秩为r的矩阵中，有可能存在等于零的r-1阶子式，如秩为2的矩阵



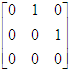
    中存在等于0的1阶子式。

  • 第14题：

    设A是nxm矩阵，B是mxn矩阵，E是n阶单位阵，若AB=E，证明B的列向量组线性无关。


    答案：
    解析：

  • 第15题：

    设A、B、C为同阶矩阵，且C为非奇异矩阵，满足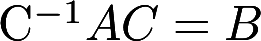，求证：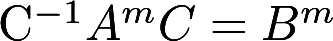


    答案：
    解析：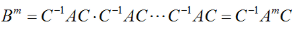

  • 第16题：

    设n阶方阵是一个上三角矩阵，则需存储的元素个数为()。

    A.n
    B.n×n
    C.n×n/2
    D.n(n+1)/2

    答案：D
    解析：
    在上三角矩阵中，第一行有1个元素，第二行有2个元素，…，第n行有n个元素，则共n(n+1)/2个。

  • 第17题：

    矩阵的LU分解就是将一个矩阵表示为一个交换下三角矩阵和一个上三角矩阵的乘积的形式。


    正确答案:正确

  • 第18题：

    设A为n阶非奇异矩阵且有分解式A=LU，其中L为单位下三角阵，U为上三角阵，求证A的所有顺序主子式均不为零。


    正确答案: 因为A非奇异，U的对角元uii不为零，又LU分解等价于高斯消去法，aii（i）=uii≠0由引理可知，矩阵A的顺序主子式均不为零。

  • 第19题：

    当满足（）条件时，矩阵A为正定矩阵。

    • A、各阶顺序主子式均大于零
    • B、各阶顺序主子式均小于零
    • C、所有偶数阶主子式大于零
    • D、所有奇数阶主子式小于零

    正确答案:A

  • 第20题：

    n阶实对称矩阵A为正定矩阵，则下列不成立的是（）。

    • A、所有k级子式为正（k=1，2，…，n）
    • B、A的所有特征值非负
    • C、秩（A）=n

    正确答案:A

  • 第21题：

    判断题
    矩阵的LU分解就是将一个矩阵表示为一个交换下三角矩阵和一个上三角矩阵的乘积的形式。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第22题：

    问答题
    由高斯消去法说明当Δi≠0（i=1，2，...，n-1）时，则A=LU，其中L为单位下三角阵，U为上三角阵。

    正确答案： 高斯消去法第k步等价于左乘单位下三角矩阵Lk，而顺序主子式均不为零保证所得矩阵对角元不为零，可进行第k+1步消元，U=A（n）=Ln...L1A，A=L1-1...Ln-1U=LU。
    解析： 暂无解析

  • 第23题：

    单选题
    当满足（）条件时，矩阵A为正定矩阵。
    A

    各阶顺序主子式均大于零

    B

    各阶顺序主子式均小于零

    C

    所有偶数阶主子式大于零

    D

    所有奇数阶主子式小于零


    正确答案： B
    解析： 暂无解析

相关内容