如果用二分法求方程x3+x-4=0在区间[1，2]内的根精确到三位小数，需对分（）次。

题目

如果用二分法求方程x3+x-4=0在区间[1，2]内的根精确到三位小数，需对分（）次。

相似考题

1.用迭代法求方程f(x)=x^3－x－1=0的根,取x0=1.5。()A、1.5B、1.35721C、1.32494D、1.32588

2.设求方程f(x)=0的根的牛顿法收敛,则它具有()收敛。A、超线性B、平方C、线性D、三次

3.设有方程f(x)=0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分法求该方程在区间[a，b]上的一个实根，采用的算法设计技术为（ ）

4.用变端点弦截法求方程f(x)=x^3－x－1=0在区间[a,b]的根。()A、1.324718B、1.315962C、1.266667D、1.5

参考答案和解析
正确答案:10
更多“如果用二分法求方程x3+x-4=0在区间[1，2]内的根精确到三位小数，需对分（）次。”相关问题

  • 第1题：

    为了用二分法求函数f(x)＝x3-2x2-0.1的根(方程f(x)＝0的解)，可以选择初始区间(64)。也就是说，通过对该区间逐次分半可以逐步求出该函数的一个根的近似值。

    A．[-2，-1]

    B．[-1，1]

    C．[1，2]

    D．[2，3]


    正确答案：D
    解析：为了用二分法求函数Rx)的根(方程f(x)＝0的解)，首先需要确定初始区间[x1，x2]，使f(x1)f(x2)≤0。其原理是：只要连续函数f(x)在某区间的两端点上符号相反，则在该区间内必存在一个根。也就是说，从负值连续变到正值必然会经过零值；从正值连续变到负值也必然要经过0值。
      f(-2)=-8-8-0.10  f(-1)＝-1-2-0.10  f(1)＝1-2-0.10
      f(2)=8-8-0.10  f(3)=27-18-0.1＞0
      所以，在区间[2，3]中必然存在f(x)的一个根，[2，3]可以作为二分法求f(x)之根的初始区间。

  • 第2题：

    设有方程f(x)一0在区间[a，b]上有实根，且f(a)与f(b)异号，利用二分化法求该方程在区间[a’b]上的一个实根，采用的算法设计技术为


    正确答案：A
    减半递推技术中所谓减半是指将问题的规模减半，而问题的性质不变；所谓“递推”，是指重复“减半’’的过程。i亥题的解题思路正是基于减半递推的思想。

  • 第3题：

    黄金分割比例精确到小数点后三位是（）。


    正确答案:0.618

  • 第4题：

    用二分法和牛顿法求x-tgx=0的最小正根。


    正确答案:求得最小正根为4.4934。

  • 第5题：

    已知两圆的方程，需联立两圆的方程求两圆交点，如果判别式＞0，则说明两圆弧有一个交点。


    正确答案:错误

  • 第6题：

    用二分法求解方程f（x）=x3-x-1=0在[1，2]的近似根，准确到10-3，要达到此精度至少迭代（）次。


    正确答案:9

  • 第7题：

    已知两圆的方程，需联立两圆的方程求两圆交点，如果判别式（），则说明两圆弧没有交点。

    • A、△=0
    • B、△＜0
    • C、△＞0
    • D、不能判断

    正确答案:A

  • 第8题：

    标准操作卡中的时间应精确到（）。

    • A、小数点后一位
    • B、小数点后两位
    • C、小数点后三位
    • D、小数点后忽略不计

    正确答案:A

  • 第9题：

    填空题
    如果用二分法求方程x3+x-4=0在区间[1，2]内的根精确到三位小数，需对分（）次。

    正确答案： 10
    解析： 暂无解析

  • 第10题：

    单选题
    二分法求f(x)=0在[α,B.]内的根,二分次数n满足（　）。
    A

    只与函数f(x)有关

    B

    只与根的分离区间以及误差限有关

    C

    与根的分离区间、误差限及函数f(x)有关

    D

    只与误差限有关


    正确答案： D
    解析： 暂无解析

  • 第11题：

    填空题
    黄金分割比例精确到小数点后三位是（）。

    正确答案： 0.618
    解析： 暂无解析

  • 第12题：

    单选题
    求方程f(x)=0在区间[0,1]内的根,要求误差不超过10-4,那么二分次数n十1≥（　）。
    A

    12

    B

    13

    C

    14

    D

    15


    正确答案： A
    解析： 暂无解析

  • 第13题：

    补充程序Ccon031.C,使其用牛顿迭代法求方程2x3－4x2＋3x－6=0在1.5附近的根。


    /**/main（）/**/
    }/**/while/**/（fabs（x-x0）>=1e-6）；

  • 第14题：

    设函数y(x)是微分方程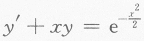满足条件y(0)=0的特解.
    　　(Ⅰ)求y(x)；
    　　(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.


    答案：
    解析：

  • 第15题：

    用二分法求方程f（x）=x3+x-1=0在区间[0，1]内的根，进行一步后根的所在区间为（），进行两步后根的所在区间为（）。


    正确答案:0.5，1；0.5，0.75

  • 第16题：

    若用二分法求方程f（x）=0区间[1，2]内的根，要求精确到第3位小数，则需要对分（）次。


    正确答案:10

  • 第17题：

    比较求ex+10x-2=0的根到三位小数所需的计算量；1）在区间[0，1]内用二分法；2）用迭代法xk+1=（2-exk）/10，取初值x0=0。


    正确答案: 1）二分14次得0.0905456；
    2）迭代5次得0.0905246。

  • 第18题：

    求S=1/1+1/2+1/3+？？+1/100（精确到小数点后三位）。


    正确答案:#include<；stdio.h>；
    M.ain（）
    {
    I.nti；
    F.loatsum=0；
    F.or（i=1；i<；=100；i++）
    {sum=sum+1.0/i；}
    P.rintf（"1/1+1/2+...+1/100=%7.3f/n"，sum）；
    }

  • 第19题：

    用天平测定宝玉石密度值时，称重值应精确到小数点后（）。

    • A、第二位
    • B、第三位
    • C、第四位

    正确答案:A

  • 第20题：

    填空题
    用二分法求方程f（x）=x3+x-1=0在区间[0，1]内的根，进行一步后根的所在区间为（），进行两步后根的所在区间为（）。

    正确答案： 0.5，1,0.5，0.75
    解析： 暂无解析

  • 第21题：

    填空题
    用二分法求解方程f（x）=x3-x-1=0在[1，2]的近似根，准确到10-3，要达到此精度至少迭代（）次。

    正确答案： 9
    解析： 暂无解析

  • 第22题：

    填空题
    若用二分法求方程f（x）=0区间[1，2]内的根，要求精确到第3位小数，则需要对分（）次。

    正确答案： 10
    解析： 暂无解析

  • 第23题：

    问答题
    比较求ex+10x-2=0的根到三位小数所需的计算量；1）在区间[0，1]内用二分法；2）用迭代法xk+1=（2-exk）/10，取初值x0=0。

    正确答案： 1）二分14次得0.0905456；
    2）迭代5次得0.0905246。
    解析： 暂无解析

相关内容