某厂准备生产一种新的电子仪器。可采用晶体管分立元件电路,也可采用集成电路。采用分立元件电路有经验,肯定成功,可获利25万元。采用集成电路没有经验,试制成功的概率为0.4。若试制成功可获利250万元,若失败,则亏损100万元。 (1)以期望损益值为标准进行决策。 (2)对先验概率进行敏感性分析。 (3)规定最大收益时效用为1,亏损最大时效用为0.决策者认为稳得25万元与第二方案期望值100万元相当。要求用效用概率决策法进行决策,并与(1)的决策结果比较。
题目
某厂准备生产一种新的电子仪器。可采用晶体管分立元件电路,也可采用集成电路。采用分立元件电路有经验,肯定成功,可获利25万元。采用集成电路没有经验,试制成功的概率为0.4。若试制成功可获利250万元,若失败,则亏损100万元。 (1)以期望损益值为标准进行决策。 (2)对先验概率进行敏感性分析。 (3)规定最大收益时效用为1,亏损最大时效用为0.决策者认为稳得25万元与第二方案期望值100万元相当。要求用效用概率决策法进行决策,并与(1)的决策结果比较。
相似考题
更多“某厂准备生产一种新的电子仪器。可采用晶体管分立元件电路,也可采用集成电路。采用分立元件电路有经验,肯定成功,可获利25万元。采用集成电路没有经验,试制成功的概率为0.4。若试制成功可获利250万元,若失败,则亏损100万元。 (1)以期望损益值为标准进行决策。 (2)对先验概率进行敏感性分析。 (3)规定最大收益时效用为1,亏损最大时效用为0.决策者认为稳得25万元与第二方案期望值100万元相当。要求用效用概率决策法进行决策,并与(1)的决策结果比较。”相关问题
-
第1题:
运用决策树决策的步骤()A. 绘制决策树图
B. 预计可能事件及其发生的概率
C. 计算各策略方案的损益期望值
D. 比较各决策方案的损益期望值,进行择优决策。
正确答案:ABCD
-
第2题:
某科研单位面临着一个是否承担及如何承担一项科研任务的选择。在经过耗资40万元的调查和论证后,能争取到任务的概率为40%;如用260万元进行开发设计,其成功的概率为80%,成功能获利600万元;失败的概率为20%,失败罚款100万元;如采用老设备改造方法,要耗资160万元,成功与失败的概率各为50%,成功能获利600万元,失败罚款同样为100万元。将这些绘制决策树如图16-2所示。在图16-2中,P表示一个决策点,良好的选择可根据计算(31)值加以比较而得出。所有方案中可能收益最大的是(32),而R点的收益期望值约为(33),N点的该期望值约为(34)。经分析计算和比较,最后的选择应是(35)。
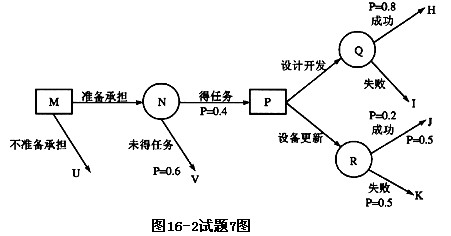
A.平均收益
B.最大收益
C.最可能收益
D.收益期望
正确答案:D
-
第3题:
共用题干
某企业为了扩大某产品的生产,拟建设新厂。据市场预测,产品销路好的概率为0.8,销路差的概率为0.2。有三种方案可供企业选择:方案1:新建大厂,需投资260万元。据初步估计,销路好时,每年可获利140万元;销路差时,每年亏损50万元。服务期为10年。方案2:新建小厂,需投资180万元。销路好时,每年可获利50万元,销路差时,每年仍可获利23万元。服务期为10年。方案3:先建小厂,3年后销路好时再扩建,需追加投资200万元,服务期为7年,估计每年获利105万元。根据以上资料,回答下列问题:材料中使用的决策方法是()。
A:线性规划法
B:盈亏平衡法
C:决策收益表法
D:决策树分析法答案:D解析:决策树分析法是指将构成决策方案的有关因素,以树状图形的方式表现出来,并据以分析和选择决策方案的一种系统分析法。材料中虽没有直接出现树状图,但运用的仍然是决策树分析法,以损益值为依据,比较不同方案的期望损益值,决定较为复杂情况下的方案的取舍。
风险型决策是指已知决策方案所需的条件,但每种方案的执行都有可能出现不同后果,多种后果的出现有一定的概率,即存在着风险。决策树分析法属于风险型决策方法。
方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)。
各方案的期望收益为:方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)方案2的期望收益为:(0.8*50+0.2*23)*10-180=266(万元)方案3:3年后扩建的期望收益为:105*7-200=535(万元);3年后不扩建的期望收益为:50*7=350(万元);故3年后销路好时,扩建比不扩建要好。方案3的期望收益为:(0.8*50*3+0.8*535+0.2*23*10)-180=414(万元)计算结果表明,在3种方案中方案1最好。
该企业采用的是决策树分析法。决策树是以决策结点为出发点,从中引出若干方案枝,每个方案枝代表一个可行方案。在各方案枝的末端有一个状态结点,从状态结点引出若干概率枝,每个概率枝表示一种自然状态。在各概率枝的末梢注有损益值。 -
第4题:
共用题干
某企业为了扩大某产品的生产,拟建设新厂。据市场预测,产品销路好的概率为0.8,销路差的概率为0.2。有三种方案可供企业选择:方案1:新建大厂,需投资260万元。据初步估计,销路好时,每年可获利140万元;销路差时,每年亏损50万元。服务期为10年。方案2:新建小厂,需投资180万元。销路好时,每年可获利50万元,销路差时,每年仍可获利23万元。服务期为10年。方案3:先建小厂,3年后销路好时再扩建,需追加投资200万元,服务期为7年,估计每年获利105万元。根据以上资料,回答下列问题:这种决策方法属于()。
A:定性决策方法
B:风险型决策方法
C:确定型决策方法
D:不确定型决策方法答案:B解析:决策树分析法是指将构成决策方案的有关因素,以树状图形的方式表现出来,并据以分析和选择决策方案的一种系统分析法。材料中虽没有直接出现树状图,但运用的仍然是决策树分析法,以损益值为依据,比较不同方案的期望损益值,决定较为复杂情况下的方案的取舍。
风险型决策是指已知决策方案所需的条件,但每种方案的执行都有可能出现不同后果,多种后果的出现有一定的概率,即存在着风险。决策树分析法属于风险型决策方法。
方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)。
各方案的期望收益为:方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)方案2的期望收益为:(0.8*50+0.2*23)*10-180=266(万元)方案3:3年后扩建的期望收益为:105*7-200=535(万元);3年后不扩建的期望收益为:50*7=350(万元);故3年后销路好时,扩建比不扩建要好。方案3的期望收益为:(0.8*50*3+0.8*535+0.2*23*10)-180=414(万元)计算结果表明,在3种方案中方案1最好。
该企业采用的是决策树分析法。决策树是以决策结点为出发点,从中引出若干方案枝,每个方案枝代表一个可行方案。在各方案枝的末端有一个状态结点,从状态结点引出若干概率枝,每个概率枝表示一种自然状态。在各概率枝的末梢注有损益值。 -
第5题:
某项目有40%的概率获利10万元,30%概率会亏损8万元,30%的概率既不获利也不亏损。该项目的预期货币价值分析(EMV)是( )。A.0元
B.1.6万元
C.2万元
D.6.4万元答案:B解析:EMV=10*40%+(-8*30%)+0*30%=1.6万元 -
第6题:
生产某种产品有两个建厂方案。(1)建大厂:需要初 期投资500万元。如果产品销路好,每年可以获利200万 元;如果销路不好,7每年会亏损20万元。(2)建小厂, 需要初期投资200万元。如果产品销路好,每年可以获利 100万元;如果销路不好,每年只能获利20万元。 市场调研表明,未来2年,这种产品销路好的概率为70%。 如果这2年销路好,则后续5年销路好的概率上升为80%; 如果这2年销路不好,则后续5年销路好的概率仅为10%。 为取得7年最大总收益,决策者应( )。A. 建大厂,总收益超500万元
B. 建大厂,总收益略多于300万元
C. 建小厂,总收益超500万元
D. 建小厂,总收益略多于300万元答案:B解析: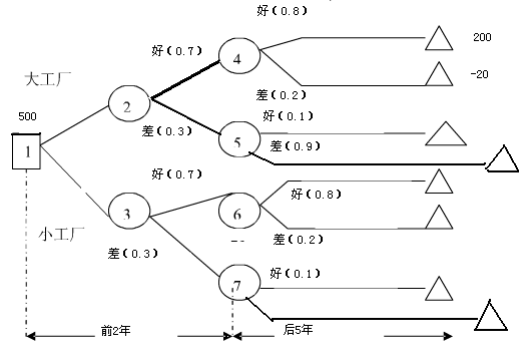

-
第7题:
某建筑工程公司拟承包一项工程,该工程可以用甲、乙、丙、丁四种施工方案中的任何一种方案完成,各种施工方案在各种天气情况下的获利情况见表1。
表1不同施工方案和自然状态时的获利情况单位:万元
假如无法预测天气情况的概率值,采用合理性标准进行决策时,则施工方案丙的期望值为()万元。A.567
B.587
C.598
D.625答案:A解析:合理性标准,又称等概率法。该法是在参考资料和统计资料不足,难以预测各种自然状态出现的概率时予以使用。此时假设各种自然状态发生的概率相等。由于该工程所在地区气象资料不全,难以预测施工期间天气状况发生的概率,则假定天气好、天气一般、天气坏这三种自然状态发生的概率相等,都为1/3则有:施工方案丙的期望值=
-
第8题:
某承包人面临A、B两项工程投标,因受本单位资源条件限制,只能选择其中一项工程投标,或者两项工程均不投标。根据过去类似工程投标的经验数据,A工程投高标的中标概率为0.3,投低标的中标概率为0.6,编制投标文件的费用为3万元;B工程投高标的中标概率为0.4,投低标的中标概率为O。7,编制投标文件的费用为2万元。各方案承包的效果、概率及损益情况见表7-2。
【问题】2、试运用决策树法进行投标决策。答案:解析:2、第一步:画出决策树,标明各方案的概率和损益值,见图7—5。第二步:计算图中各机会点的期望值(可将计算结果标在各机会点上方)。点⑦:150×0.3+100×0.5+50×0.2=105万元点②:105×0.3-3×O。7=29.4万元点⑧:110×0.2+60×0.7+0×O.1=64万元点③:64×0.6-3×0.4=37.2万元点⑨:110×0.4+70×0.5+30×0.1=82万元点④:82×0.4-2×O.6=31.6万元点⑩:470×0.2+30×O.5-10×0.3=26万元点⑤:26×0.7-2×0.3=27.6万元点⑥:O第三步:选择最优方案。因为点③的期望值最大,故投A工程低标为最优方案。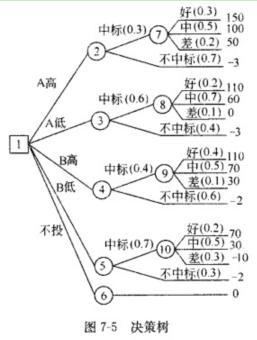
-
第9题:
一家食品公司考虑向市场投放一种新食品,以增加供应品种。销售研究部门认为,若销量好(概率为0.7)每月可获利50万元;若销量不好(概率为0.3)每月将亏损28万元。现有两个可能策略: (1)根据现有信息,立即决定是否销售新食品; (2)自己进行可靠性为70%的市场调查,调查费用为2万元;要不要进行市场调查?
正确答案:不调查期望收益为26.6万元,进行调查的期望收益为24.6万元,所以不需要进行市场调查。 -
第10题:
某企业拟开发新产品,现在有两个可行性方案需要决策。 方案甲:开发新产品A,需要追加投资500万元,经营期限为5年。在期间的每一年,产品销路好可获利300万元;销路一般可获利120万元;销路差可获利-25万元。三种情况的概率分别为30%,50%,20%。 方案乙:开发新产品B,需要追加投资300万元,经营期限为5年。在期间的每一年,产品销路好可获利100万元;销路一般可获利70万元;销路差可获利30万元。三种情况的概率分别为60%,30%,10%。 你觉得下面哪个是正确的?()
- A、方案甲的期望值为145万元;净收益值为-355万元。方案乙的期望值为84万元、净收益值为-216万元。选择甲方案。
- B、方案甲的期望值为725万元、净收益值为725万元;方案乙的期望值为420万元、净收益值为420万元。选择乙方案。
- C、方案甲的期望值为725万元、净收益值为225万元;方案乙的期望值为420万元;净收益值为120万元。选择甲方案。
- D、方案甲的期望值为1975万元、净收益值为1475万元;方案乙的期望值为1000万元、净收益值为700万元。选择甲方案。
正确答案:C -
第11题:
问答题某厂准备生产一种新的电子仪器。可采用晶体管分立元件电路,也可采用集成电路。采用分立元件电路有经验,肯定成功,可获利25万元。采用集成电路没有经验,试制成功的概率为0.4。若试制成功可获利250万元,若失败,则亏损100万元。决策者认为稳得25万元与方案0.7的概率获得250万,0.3的概率亏损100万的效用相当,试用效用概率决策法进行决策.正确答案: 1)晶体管分立元件电路期望收益25万,集成电路期望收益
0.4*250+0.6*(-100)=40万采用集成电路方案
2)试验成功概率P
P*250+(1-P)*(-100)>25,P>0.357。所以P>0.357时选择集成电路方案,否则选择另一个方案
3)u(-100)=0,u(250)=1,u(25)=0.7*u(250)+0.3*u(-100)=0.7
晶体管分立元件电路期望效用0.7,集成电路期望效用:
0.4*1+0.6*0=0.4,采用晶体管分立元件电路方案。解析: 暂无解析 -
第12题:
单选题下列有关决策收益表法的表述错误的是()。A决策收益表法又称决策损益矩阵
B损益期望值实质上是各种状态下加权性质的平均值
C利用表格的形式,进行期望值比较和选择的决策方法是决策收益表法
D当决策指标为成本时,应选取期望值最大的方案
正确答案: D解析: 当决策指标为收益时,应选取期望值最大的方案;当决策指标为成本时,应选取期望值最小的方案。 -
第13题:
某企业拟开发新产品,现在有两个可行性方案需要决策。
方案甲:开发新产品A,需要追加投资500万元,经营期限为5年。在期间的每一年,产品销路好可获利300万元;销路一般可获利120万元;销路差可获利-25万元。三种情况的概率分别为30%,50%,20%。
方案乙:开发新产品B,需要追加投资300万元,经营期限为5年。在期间的每一年,产品销路好可获利100万元;销路一般可获利70万元;销路差可获利30万元。三种情况的概率分别为60%,30%,10%。
A.方案甲的期望值为145万元;净收益值为-355万元。方案乙的期望值为84万元、净收益值为-216万元。选择甲方案。
B.方案甲的期望值为725万元、净收益值为725万元;方案乙的期望值为420万元、净收益值为420万元。选择乙方案。
C.方案甲的期望值为725万元、净收益值为225万元;方案乙的期望值为420万元;净收益值为120万元。选择甲方案。
D.方案甲的期望值为1975万元、净收益值为1475万元;方案乙的期望值为1000万元、净收益值为700万元。选择甲方案
参考答案:C
-
第14题:
某企业为了扩大某产品的生产,拟建设新厂。据市场预测,产品销路好的概率为0.8,销路差的概率为0.2。有三种方案可供企业选择:
方案1:新建大厂,需投资260万元。据初步估计,销路好时,每年可获利140万元;销路差时,每年亏损50万元。服务期为10年。
方案2:新建小厂,需投资180万元。销路好时,每年可获利50万元,销路差时,每年仍可获利23万元。服务期为10年。
方案3:先建小厂,3年后销路好时再扩建,需追加投资200万元,服务期为7年,估计每年获利105万元。
根据以上材料,回答 96~100 题
第 96 题 材料中使用的决策方法是( )。
A.线性规划法
B.盈亏平衡法
C.决策收益表法
D.决策树分析法
正确答案:D
决策树分析法是指将构成决策方案的有关因素,以树状图形的方式表现出来,并据以分析和选择决策方案的一种系统分析法。材料中虽没有直接出现树状图,但运用的仍然是决策树分析法,以损益值为依据,比较不同方案的期望损益值,决定较为复杂情况下的方案的取舍。故选D -
第15题:
共用题干
某企业为了扩大某产品的生产,拟建设新厂。据市场预测,产品销路好的概率为0.8,销路差的概率为0.2。有三种方案可供企业选择:方案1:新建大厂,需投资260万元。据初步估计,销路好时,每年可获利140万元;销路差时,每年亏损50万元。服务期为10年。方案2:新建小厂,需投资180万元。销路好时,每年可获利50万元,销路差时,每年仍可获利23万元。服务期为10年。方案3:先建小厂,3年后销路好时再扩建,需追加投资200万元,服务期为7年,估计每年获利105万元。根据以上资料,回答下列问题:如果该企业选取方案1,则方案1的期望收益为()万元。
A:760
B:800
C:820
D:860答案:A解析:决策树分析法是指将构成决策方案的有关因素,以树状图形的方式表现出来,并据以分析和选择决策方案的一种系统分析法。材料中虽没有直接出现树状图,但运用的仍然是决策树分析法,以损益值为依据,比较不同方案的期望损益值,决定较为复杂情况下的方案的取舍。
风险型决策是指已知决策方案所需的条件,但每种方案的执行都有可能出现不同后果,多种后果的出现有一定的概率,即存在着风险。决策树分析法属于风险型决策方法。
方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)。
各方案的期望收益为:方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)方案2的期望收益为:(0.8*50+0.2*23)*10-180=266(万元)方案3:3年后扩建的期望收益为:105*7-200=535(万元);3年后不扩建的期望收益为:50*7=350(万元);故3年后销路好时,扩建比不扩建要好。方案3的期望收益为:(0.8*50*3+0.8*535+0.2*23*10)-180=414(万元)计算结果表明,在3种方案中方案1最好。
该企业采用的是决策树分析法。决策树是以决策结点为出发点,从中引出若干方案枝,每个方案枝代表一个可行方案。在各方案枝的末端有一个状态结点,从状态结点引出若干概率枝,每个概率枝表示一种自然状态。在各概率枝的末梢注有损益值。 -
第16题:
共用题干
某企业为了扩大某产品的生产,拟建设新厂。据市场预测,产品销路好的概率为0.8,销路差的概率为0.2。有三种方案可供企业选择:方案1:新建大厂,需投资260万元。据初步估计,销路好时,每年可获利140万元;销路差时,每年亏损50万元。服务期为10年。方案2:新建小厂,需投资180万元。销路好时,每年可获利50万元,销路差时,每年仍可获利23万元。服务期为10年。方案3:先建小厂,3年后销路好时再扩建,需追加投资200万元,服务期为7年,估计每年获利105万元。根据以上资料,回答下列问题:下列选项中,属于该企业所采用的决策方法的构成要素包括()。
A:决策结点
B:方案枝
C:状态结点
D:市场状态答案:A,B,C解析:决策树分析法是指将构成决策方案的有关因素,以树状图形的方式表现出来,并据以分析和选择决策方案的一种系统分析法。材料中虽没有直接出现树状图,但运用的仍然是决策树分析法,以损益值为依据,比较不同方案的期望损益值,决定较为复杂情况下的方案的取舍。
风险型决策是指已知决策方案所需的条件,但每种方案的执行都有可能出现不同后果,多种后果的出现有一定的概率,即存在着风险。决策树分析法属于风险型决策方法。
方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)。
各方案的期望收益为:方案1的期望收益为:[0.8*140+0.2*(-50)]*10-260=760(万元)方案2的期望收益为:(0.8*50+0.2*23)*10-180=266(万元)方案3:3年后扩建的期望收益为:105*7-200=535(万元);3年后不扩建的期望收益为:50*7=350(万元);故3年后销路好时,扩建比不扩建要好。方案3的期望收益为:(0.8*50*3+0.8*535+0.2*23*10)-180=414(万元)计算结果表明,在3种方案中方案1最好。
该企业采用的是决策树分析法。决策树是以决策结点为出发点,从中引出若干方案枝,每个方案枝代表一个可行方案。在各方案枝的末端有一个状态结点,从状态结点引出若干概率枝,每个概率枝表示一种自然状态。在各概率枝的末梢注有损益值。 -
第17题:
生产某种产品有两个建厂方案。(1)建大厂:需要初期投资500万元。如果产品销路好,每年可以获利200万元;如果销路不好,7每年会亏损20万元。(2)建小厂,需要初期投资200万元。如果产品销路好,每年可以获利100万元;如果销路不好,每年只能获利20万元。市场调研表明,未来2年,这种产品销路好的概率为70%。如果这2年销路好,则后续5年销路好的概率上升为80%;如果这2年销路不好,则后续5年销路好的概率仅为10%。为取得7年最大总收益,决策者应( )。A. 建大厂,总收益超500万元
B. 建大厂,总收益略多于300万元
C. 建小厂,总收益超500万元
D. 建小厂,总收益略多于300万元答案:B解析:计算E4=200*5*0.8+(-20)*5*0.2=780E5=200*5*0.1+(-20)*5*0.9=10E2=0.7*780+0.7*200*2+(-20)*0.3*2+*0.3*10=817大厂7年:817-500=317 E6=0.8*100*5+0.2*20*5=420E7=0.1*100*5+0.9*20*5=140E3=0.7*420+0.7*100*2+0.3*140+0.3*20*2=488小厂:488-200=288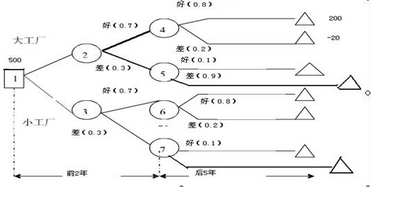
-
第18题:
某建筑工程公司拟承包一项工程,该工程可以用甲、乙、丙、丁四种施工方案中的任何一种方案完成,各种施工方案在各种天气情况下的获利情况见表1。
表1不同施工方案和自然状态时的获利情况单位:万元
若该公司在此期间不承包此项工程而去做其他工作,预测可获利650万元。根据资料预测到施工期间天气好、天气一般和天气坏的概率分别为0.5、0.4和0.1,则按照期望值标准进行决策时,关于决策选择的说法,正确的为()。A.应选择甲方案
B.应选择甲或乙方案
C.应选择乙或丙方案
D.若选择丁方案,则不如转而去做其他工作答案:A,D解析:期望值标准,是指根据风险型决策问题给定的条件,计算每个方案的期望值,然后选择收益最大或损失最小的方案作为最优方案。选择甲方案承包该工程的期望值=1200×0.5+1000×0.4-600×0.1=940(万元);选择乙方案承包该工程的期望值
=500×0.5+800×0.4+700×0.1=640(万元);选择丙方案承包该工程的期望值
=700×0.5+600×0.4+400×0.1=630(万元);选择丁方案承包该工程的期望值
=600×0.5+600×0.4+600×0.1=600(万元);不承包此项工程而去做其他工作的期望值为650万元。由于选择甲方案承包该工程的期望值最大为940万元,因此,应选择甲方案。 -
第19题:
某项目有40%的概率获利10万元,30%的概率会亏损8万元,30%的概率既不获利也不亏损,该项目的预期货币价值分析(EMV)是()。A.0元
B.1.6万元
C.2万元
D.6.4万元答案:B解析:本题考查的是定量风险分析中的决策的分类与模型,正确选项为B:1.6万元。
每个可能结果的数值与其发生概率相乘之后加总,即得出预期货币价值。
EMA=10x40%+(-8)x30%+0x30%=4+(-2.4)=1.6万元 -
第20题:
一家食品公司考虑向市场投放一种新食品,以增加供应品种。销售研究部门认为,若销量好(概率为0.7)每月可获利50万元;若销量不好(概率为0.3)每月将亏损28万元。现有两个可能策略: (1)根据现有信息,立即决定是否销售新食品; (2)自己进行可靠性为70%的市场调查,调查费用为2万元;要不要投放新产品。
正确答案:应当投放新产品,其期望收益为26.6万元。 -
第21题:
下列有关决策收益表法的表述错误的是()。
- A、决策收益表法又称决策损益矩阵
- B、损益期望值实质上是各种状态下加权性质的平均值
- C、利用表格的形式,进行期望值比较和选择的决策方法是决策收益表法
- D、当决策指标为成本时,应选取期望值最大的方案
正确答案:D -
第22题:
问答题一家食品公司考虑向市场投放一种新食品,以增加供应品种。销售研究部门认为,若销量好(概率为0.7)每月可获利50万元;若销量不好(概率为0.3)每月将亏损28万元。现有两个可能策略: (1)根据现有信息,立即决定是否销售新食品; (2)自己进行可靠性为70%的市场调查,调查费用为2万元;要不要进行市场调查?正确答案: 不调查期望收益为26.6万元,进行调查的期望收益为24.6万元,所以不需要进行市场调查。解析: 暂无解析 -
第23题:
问答题一家食品公司考虑向市场投放一种新食品,以增加供应品种。销售研究部门认为,若销量好(概率为0.7)每月可获利50万元;若销量不好(概率为0.3)每月将亏损28万元。现有两个可能策略: (1)根据现有信息,立即决定是否销售新食品; (2)自己进行可靠性为70%的市场调查,调查费用为2万元;要不要投放新产品。正确答案: 应当投放新产品,其期望收益为26.6万元。解析: 暂无解析 -
第24题:
单选题一个保守的决策者具有财富10万元,他的效用函数u(x)=x-0.02x2,0≤x≤25,这个决策者有机会用5万元进行投资,投资收益可以以0.5的概率获得20万元,或者一无所获。下列说法中正确的是( )。(1)决策者不会进行投资;(2)如果决策者有6万元的财富,他将进行投资;(3)如果决策者投资6万元,他将有正的收益。A(1)
B(1)(2)
C(1)(3)
D(2)(3)
E(1)(2)(3)
正确答案: A解析:
(1)决策者不进行投资时的效用价值为:
u(10)=x-0.02x2|x=10=8
决策者的财富在投资后的效用价值为:
E[u(10-5+X)] =E[u(5+X)]
=0.5×(5+x-0.02(5+x)2)|x=20+0.5×(5+x-0.02(5+x)2)|x=0
=0.5×(25-0.02×252)+0.5×(5-0.02×52)
=8.5,
即 E(u(10-5+X))>u(10),决策者将会选择投资;
(2)如果决策者有6万元的财富,则决策者不进行投资时的效用价值为:
u(6)=x-0.02x2|x=6=5.28
投资后决策者的效用价值为:
E[u(6-5+X)]=E[u(1+X)]
=0.5×(1-0.02)+0.5×(21-0.02×212)
=6.58,
即 E[u(6-5+X)]>u(6),决策者将会选择投资;
(3)在决策者投资6万元的情况下,则:
E[u(10-6+X)]=E[u(4+X)]
=0.5×(4-0.02×42)+0.5×(24-0.02×242)
=8.08>u(10)=8,
即投资6万元有正的收益。
