在正态检验中，概率坐标纸上得到一条近似直线，均值所对应的纵坐标F（x）（％）的值为（）。

题目

在正态检验中，概率坐标纸上得到一条近似直线，均值所对应的纵坐标F（x）（％）的值为（）。

相似考题

1.对正态总体参数估计的描述正确的是( )。A．正态均值μ的无偏估计有两个，一个是样本均值的估计，另一个是样本中位数的估计，即μ(2＝Me＝(1/n)(X1+X2+…+Xn)B．对正态均值μ来说，样本均值总比样本中位数更有效，应舍去样本中位数C．在实际过程中，应优先选用样本均值去估计正态均值μ。但有时在现场，为了简便快捷，选用样本中位数去估计正态均值μ也是有的D．正态方差σ2的无偏估计常用的只有一个，就是样本方差S2

2.从任一非正态总体中随机抽取一个大样本观测“身高”变量,则以下正确的有()A.样本均值的抽样分布近似为F分布B.样本均值的抽样分布近似为卡方分布C.样本均值的抽样分布为严格的正态分布D.样本均值的抽样分布近似为正态分布E.样本数据有可能是正态分布

3.关于基于秩次的非参数检验,下列说法错误的是( )A、符号秩和检验中，差值为零不参加编秩B、两样本比较的秩和检验方法中的正态近似法为参数检验C、当符合正态假定时，非参数检验犯Ⅱ类错误的概率较参数检验大D、当样本足够大时，秩和分布近似正态E、秩和检验适用于检验等级资料、可排序资料和分布不明资料的差异

4.以下情况可以用Z统计量检验的有( )。A总体均值的检验，小样本B正态总体均值的检验，小样本，方差未知C大样本总体均值的检验D正态总体方差的检验

更多“在正态检验中，概率坐标纸上得到一条近似直线，均值所对应的纵坐标F（x）（％）的值为（）。”相关问题

  • 第1题：

    在假设检验中，方差已知的正态总体均值的检验要计算Z统计量。()


    答案：(错)

  • 第2题：

    某样本数据在正态纸上描点，目测这些点在一直线附近，表示数据来自于正态总体，现从纵坐标轴上取值为0.5，则其对应于近似直线上点的横坐标是正态总体( )的估计值。

    A.标准差σ

    B.均值μ

    C.μ+σ

    D.μ+2σ


    正确答案：B

  • 第3题：

    当对正态总体均值检验时，如果总体方差未知，在小样本情况下应采用（）。

    A.z检验
    B.F检验
    C.t检验
    D.X2检验

    答案：C
    解析：
    当对正态总体均值检验时，如果总体方差未知，在小样本情况下，应采用t检验；在大样本情况下，采用2检验。

  • 第4题：

    正态概率纸的作用有（ ）。
    A.检验一个样本是否来自正态分布 B.检验一个样本是否来自二项分布
    C.检验一个样本是否来自对数正态分布
    D.若描点呈直线状，可在图上作正态均值μ的估计
    E.若描点呈直线状，可在图上作正态标准差σ的估计


    答案：A,C,D,E
    解析：

  • 第5题：

    关于基于秩次的非参数检验，下列说法错误的是（）

    A符号秩和检验中，差值为零不参加编秩

    B两样本比较的秩和检验方法中的正态近似法为参数检验

    C当符合正态假定时，非参数检验犯II类错误的概率较参数检验大

    D当样本足够大时，秩和分布近似正态

    E秩和检验适用于检验等级资料、可排序资料和分布不明资料的差异


    B
    略

  • 第6题：

    正态频率曲线在普通格纸上是一条直线。


    正确答案:错误

  • 第7题：

    当总体方差已知，无论样本容量n的大小如何，进行正态总体均值的区间估计应采用的临界值为（）

    • A、F值
    • B、Z值
    • C、T值
    • D、x2值

    正确答案:B

  • 第8题：

    以下问题可以用Z检验的有（）。

    • A、正态总体均值的检验，方差已知
    • B、正态总体均值的检验，方差未知
    • C、大样本下总体均值的检验
    • D、正态总体方差的检验

    正确答案:A,C

  • 第9题：

    当对正态总体均值检验时，如果总体方差未知则应该进行（）。

    • A、z检验
    • B、F检验
    • C、t检验
    • D、X2检验

    正确答案:C

  • 第10题：

    问答题
    从一正态总体X中抽取容量为10的样本，假设有2%的样本均值与总体均值之差的绝对值大于4，求总体的标准差.

    正确答案：
    解析：

  • 第11题：

    多选题
    抗拉强度是A产品的关键质量特性之一，三条生产线同时生产A产品，项目组想知道三条生产线所产出的A产品之抗拉强度是否具有统计意义上的差异，且其中有一条生产线的数据为非正态，下面哪种分析方法更适合（）？
    A

    t检验样本是正态

    B

    Mann-Whitney检验两个样本，可以非正态

    C

    单因子方差分析多个样本均值比较

    D

    Kruskal-Wallis检验单个总体的均值检验


    正确答案： C,A
    解析： 暂无解析

  • 第12题：

    多选题
    下列关于t检验法的说法中，正确的是（）。
    A

    进行检验的资料必须代表各连续变量

    B

    主要运用于正态总体均值的检验和两个正态总体的均值之差的检验

    C

    是一种非参数统计方法

    D

    总体方差未知，正态总体均值的检验公式。


    正确答案： C,D
    解析： 暂无解析

  • 第13题：

    在确认了某个分布是正态分布后，利用求正态均值μ与正态标准差σ的估计（ ）。

    A.从纵轴为0．50处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是正态均值μ的估计值

    B.从纵轴为0．618处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就正态均值μ的估计值

    C.从纵轴为0．84处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是正态均值μ的估计值

    D.从纵轴为0．84处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是μ+σ的估计值

    E.从纵轴为O．50处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是μ+σ的估计值


    正确答案：AD

  • 第14题：

    设正态总体X的方差为1,根据来自总体X的容量为100的简单随机样本测得样本的均值为5,则总体X的数学期望的置信度近似等于0.95的置信区间为_______.


    答案：1、(4.804 2、5.196)
    解析：
    X～N（μ，1），取统计量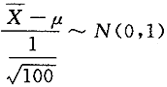，则μ的置信度为0.95的置信区间为　　

  • 第15题：

    在对单个正态总体均值的假设检验中，当总体方差已知时，选用()



    答案：B
    解析：

  • 第16题：

    某样本数据在正态纸上描点，目测这些点在一直线附近，表示数据来自于正态总体，现从纵坐标轴上取概率为0.5，则其对应于近似直线上点的横坐标是正态总体（ ）的估计。
    A.标准差σ B.均值μ C. μ+σ D.μ－σ


    答案：B
    解析：
    正态分布的均值是其分布的中心位置，概率密度函数曲线下的面积的一半为0. 5，所以在正态概率纸上概率为0. 5处对应的就是均值μ的估计值。

  • 第17题：

    设有两个来自不同正态总体的样本，X：-4.4，4.0，2.0，-4.8Y：6.0，1.0，3.2，-0.4如果要检验两个样本是否来自同一总体，则下面选项中正确的是（）。

    • A、用正态u统计量检验均值是否相同
    • B、先用χ2统计量检验方差是否相同，再用t统计量检验均值是否相同
    • C、先用χ2统计量检验方差是否相同，再用正态u统计量检验均值是否相同
    • D、先用F统计量检验方差是否相同，再用正态u统计量检验均值是否相同
    • E、先用F统计量检验方差是否相同，再用t统计量检验均值是否相同

    正确答案:E

  • 第18题：

    在大样本情况下，对方差已知的非正态总体的均值进行区间估计或假设检验使用的统计量是（）

    • A、正态统计量
    • B、X2统计量
    • C、T统计量
    • D、F统计量

    正确答案:A

  • 第19题：

    当样本容量足够大时，允许我们使用正态概率分布来近似样本均值和样本成数的抽样分布，这种定理是（）。

    • A、近似定理
    • B、正态概率定理
    • C、中心极限定理
    • D、中心正态定理

    正确答案:C

  • 第20题：

    某医生选择适当资料计算相应指标，进行t检验。进行t检验的资料应满足的条件是（）。

    • A、负偏态资料
    • B、正偏态资料
    • C、偏态资料
    • D、正态或近似正态资料
    • E、以上都不是

    正确答案:D

  • 第21题：

    假设正态总体方差未知，欲对其均值进行区间估计或假设检验。从其中抽取较小样本后使用的统计量是（）

    • A、正态统计量
    • B、x2统计量
    • C、T统计量
    • D、F统计量

    正确答案:C

  • 第22题：

    多选题
    在确认了某个分布是正态分布后，利用求正态均值μ与正态标准差σ的估计(　　)。
    A

    从纵轴为0．50处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是正态均值μ的估计值

    B

    从纵轴为0．618处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就正态均值μ的估计值

    C

    从纵轴为0．84处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是正态均值μ的估计值

    D

    从纵轴为0．84处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是μ+σ的估计值

    E

    从纵轴为O．50处画一水平线与用目测法所做的直线交与一点，过这点做垂线，垂足的坐标就是μ+σ的估计值


    正确答案： A,B
    解析： 暂无解析

  • 第23题：

    填空题
    在正态检验中，概率坐标纸上得到一条近似直线，均值所对应的纵坐标F（x）（％）的值为（）。

    正确答案： 0.5
    解析： 暂无解析

相关内容