截面为300mm×500mm的钢筋混凝土梁，净跨度为L0=6m，承受均面荷载500kN/㎡支撑在370mm厚的砖墙上，按满压墙计算，计算砖墙的局部受压应力。砖墙的局部受压面积为（）㎡。A、0.16B、0.15C、0.13D、0.11

题目

截面为300mm×500mm的钢筋混凝土梁，净跨度为L0=6m，承受均面荷载500kN/㎡支撑在370mm厚的砖墙上，按满压墙计算，计算砖墙的局部受压应力。砖墙的局部受压面积为（）㎡。

  • A、0.16
  • B、0.15
  • C、0.13
  • D、0.11
相似考题

1.某窗间墙截面尺寸为1000mm×240mm,采用MU10级砖、M5级混合砂浆砌筑,施工质量控制等级为B级,墙上支承钢筋混凝土梁,支承长度240mm,梁截面尺寸b×h=200mm×500mm,梁端支承压力的设计值为50kN,上部荷载传来的轴力设计值为120kN,试验算梁端局部受压承载力。

2.如图所示，截面尺寸为240mmX250mm的钢筋混凝土柱，支承在490mm厚的砖墙上，墙采用MU10砲块、M2.5混合砂浆砌筑，可能最先发生局部受压破坏的是哪个图所示的砖墙？

3.某钢筋混凝土深梁截面尺寸bh=250mm3000mm，1=6000mm，支承于两端砖砌纵墙上，如图所示。墙厚240mm，由MU25烧结普通砖及M10水泥砂浆砌筑。梁端支反力N1=280kN，纵墙上部竖向荷载平均压应力=0.8MPa。砌体施工质量控制等级为B级，结构安全等级二级。 1.试问，梁端局部受压承载力（kN），与下列何项数值最为接近？（　　）A、270 B、282 C、167 D、240

4.如图所示某梁截面尺寸为 250mm×550mm，支承在具有壁柱的砖墙上，支承长度 a=370mm，Nl=60kN，σ0=0.48N/mm2，采用 MU10 砖及 M2.5 混合砂浆。试验算梁端受压局部承载力。

参考答案和解析
正确答案:A
更多“截面为300mm×500mm的钢筋混凝土梁，净跨度为L0=6m，承受均面荷载500kN/㎡支撑在370mm厚的砖墙上，按满压墙计算，计算砖墙的局部受压应力。砖墙的局部受压面积为（）㎡。A、0.16B、0.15C、0.13D、0.11”相关问题

  • 第1题：

    钢筋混凝土简支矩形截面梁尺寸为250mm×500mm，混凝土强度等级为C30，梁受拉区配置3Φ20的钢筋（As=942mm2），混凝土保护层c＝25mm，承受均布荷载，梁的计算跨度l0＝6m。

    2.若已知裂缝间纵向受拉钢筋应变不均匀系数ψ＝0.825，则该梁的短期效应刚度最接近于（　　）kN·m2。

    A、27657
    B、22702
    C、22610
    D、23610

    答案：A
    解析：
    根据《混凝土结构设计规范》（GB 50010—2010）第7.2.3条规定，钢筋弹性模量与混凝土模量的比值为：



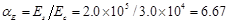
    对于矩形截面，γf＝0；纵向受拉钢筋配筋率为：



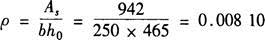
    根据式（7.2.3-1）计算，钢筋混凝土受弯构件的短期刚度为：



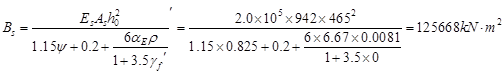
    式中，γf为受拉翼缘截面面积与腹板有效截面面积的比值。由此可知，A项数值最为接近。

  • 第2题：

    钢筋混凝土简支矩形截面梁尺寸为250mm×500mm，混凝土强度等级为C30，梁受拉区配置3Φ20的钢筋（As=942mm2），混凝土保护层c＝25mm，承受均布荷载，梁的计算跨度l0＝6m。

    1.若已知按荷载效应的准永久组合计算的跨中弯矩值Mq＝100kN·m，则裂缝间纵向受拉钢筋应变不均匀系数ψ最接近于（　　）。

    A、0.580
    B、0.635
    C、0.660
    D、0.771

    答案：D
    解析：
    已知强度等级为C30的混凝土，根据《混凝土结构设计规范》（GB 50010—2010）第4.1.3条表4.1.3-2可知，轴心抗拉强度标准值为ftk＝2.01N/mm2；根据第4.1.5条表4.1.5可知，弹性模量



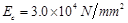
    根据第4.2.5条表4.2.5可知，钢筋的弹性模量为



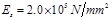
    根据第7.1.4条式（7.1.4-3）计算，则裂缝截面处纵向受拉钢筋重心处的拉应力为：



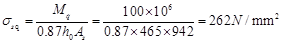
    根据第7.1.4条规定，有效受拉混凝土截面面积Ate＝0.5×b×h＝0.5×250×500＝62500mm2；根据第7.1.2条公式（7.1.2-4）计算，纵向受拉钢筋配筋率为：



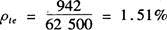
    故可计算得裂缝间纵向受拉钢筋应变不均匀系数为：



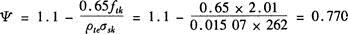
    由此可知，D项数值最为接近。

  • 第3题：

    钢筋混凝土简支矩形截面梁尺寸为250mm×500mm，混凝土强度等级为C30，梁受拉区配置3Φ20的钢筋（As=942mm2），混凝土保护层c＝25mm，承受均布荷载，梁的计算跨度l0＝6m。

    若已知梁的短期效应刚度Bs＝29732.14kN·m2，按荷载效应的标准组合计算的跨中弯矩值Mk＝90kN·m，按荷载效应的准永久组合计算的跨中弯矩值Mq＝50kN·m，梁受压区配有218的钢筋，则跨中挠度最接近于（　　）mm。


    A.10.2
    B.14.3
    C.16.3
    D.17.9

    答案：C
    解析：
    根据《混凝土结构设计规范》（GB 50010—2010）第7.2.3条规定，钢筋混凝土受弯构件的配筋率为：



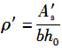
    纵向受拉钢筋配筋率为：



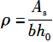
    根据第7.2.5条第1款规定，荷载长期效应组合对挠度增大的影响系数为：



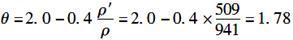
    根据第7.2.2条式（7.2.2-1）计算，受弯构件的长期刚度为：




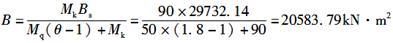
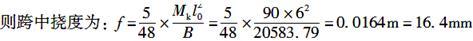
    由此可知，C项数值最为接近。

  • 第4题：

    某一间支梁，截面尺寸200mm×400mm，净跨度L0=8m，上面承受均布荷载为1200kN/m，计算最大弯矩及支座反力？梁的计算跨度按1.05L0计算，计算跨度为（）m。

    • A、8.1
    • B、8.2
    • C、8.3
    • D、8.4

    正确答案:D

  • 第5题：

    某一间支梁，截面尺寸200mm×400mm，净跨度L0=8m，上面承受均布荷载为1200kN/m，计算最大弯矩及支座反力？梁的均布线荷载为（）kN/m。

    • A、215
    • B、220
    • C、230
    • D、240

    正确答案:D

  • 第6题：

    截面为300mm×500mm的钢筋混凝土梁，净跨度为L0=6m，承受均面荷载500kN/㎡支撑在370mm厚的砖墙上，按满压墙计算，计算砖墙的局部受压应力。梁的均布线荷载为（）kN/m。

    • A、120
    • B、130
    • C、150
    • D、160

    正确答案:C

  • 第7题：

    某一间支梁，截面尺寸200mm×400mm，净跨度L0=8m，上面承受均布荷载为1200kN/m，计算最大弯矩及支座反力？梁的最大弯矩为（）kN.m。

    • A、2116.8
    • B、2117.2
    • C、2117.8
    • D、2118.4

    正确答案:A

  • 第8题：

    预应力先张法施工时，台座横梁按（）。

    • A、承受集中荷载的简支梁计算
    • B、承受集中荷载的连续梁计算
    • C、承受均布荷载的简支梁计算
    • D、承受均布荷载的连续梁计算

    正确答案:C

  • 第9题：

    某240mm厚砖墙上支承跨度为5.7m的钢筋混凝土梁，为提高梁端下砌体的局部承载力，釆取下列措施中何者更为经济、有效？（）

    • A、增加墙厚
    • B、增加梁宽
    • C、增加梁端搁置长度
    • D、在梁端下设置预制刚性垫块

    正确答案:D

  • 第10题：

    作用在垫梁上的局部荷载可分为沿砌体墙厚（）分布和沿墙厚（）分布两种情况。前者如等跨连续梁中支座下的砌体局部受压；后者如单跨简支梁或连续梁端部支座下砌体的局部受压。


    正确答案:均匀；不均匀

  • 第11题：

    单选题
    预应力先张法施工时，台座横梁按（）。
    A

    承受集中荷载的简支梁计算

    B

    承受集中荷载的连续梁计算

    C

    承受均布荷载的简支梁计算

    D

    承受均布荷载的连续梁计算


    正确答案： D
    解析： 暂无解析

  • 第12题：

    填空题
    作用在垫梁上的局部荷载可分为沿砌体墙厚（）分布和沿墙厚（）分布两种情况。前者如等跨连续梁中支座下的砌体局部受压；后者如单跨简支梁或连续梁端部支座下砌体的局部受压。

    正确答案： 均匀,不均匀
    解析： 暂无解析

  • 第13题：

    某跨度9m，开间4m的单层单跨砌体结构（见图），总长32m，承重纵墙厚370mm，采用MU15普通砖，M5水泥砂浆砌筑，墙高H=3.8m，窗间墙宽2m，高3m，每隔4m有一钢筋混凝土梁支承于窗间墙上，上铺空心预制板，大梁截面尺寸b×h=200mm×550mm，梁端伸入墙内240mm。梁端支承压力设计值Nl=80kN，檐沟等自重在梁底截面产生的平均压应力σ0=0.3N/mm2。



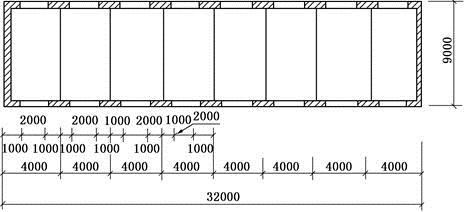
    2.梁端设置预制混凝土垫块，ab=240mm、bb=500mm、tb=300mm，垫块下砌体的局部受压承载力最接近于（　　）kN。

    A、135
    B、145
    C、155
    D、165

    答案：C
    解析：

  • 第14题：

    钢筋混凝土简支矩形截面梁尺寸为250mm×500mm，混凝土强度等级为C30，梁受拉区配置3Φ20的钢筋（As=942mm2），混凝土保护层c＝25mm，承受均布荷载，梁的计算跨度l0＝6m。

    若已知梁的短期效应刚度Bs＝29732.14kN·m2，按荷载效应的标准组合计算的跨中弯矩值Mk＝90kN·m，按荷载效应的准永久组合计算的跨中弯矩值Mq＝50kN·m，梁受压区配有218的钢筋，则跨中挠度最接近于（　　）mm。


    A、10.2
    B、14.3
    C、16.3
    D、17.9

    答案：C
    解析：
    根据《混凝土结构设计规范》（GB 50010—2010）第7.2.3条规定，钢筋混凝土受弯构件的配筋率为：



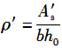
    纵向受拉钢筋配筋率为：



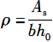
    根据第7.2.5条第1款规定，荷载长期效应组合对挠度增大的影响系数为：



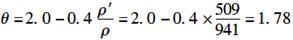
    根据第7.2.2条式（7.2.2-1）计算，受弯构件的长期刚度为：




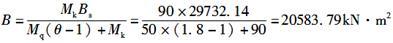
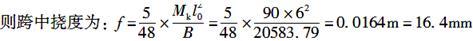
    由此可知，C项数值最为接近。

  • 第15题：

    按下列条件确定。图为某办公楼底层局部承重横墙的示意图。墙体厚240mm，横墙间距6m，采用Mu10普通砖、M5混合砂浆砌筑。
    试验算外纵墙上截面为b×h=240mm×400mm的钢筋混凝土挑梁下砖砌体的局部受压承载力（kN），并指出其值与下列何项数值最为接近？（　　）

    A.132.7
    B.159.3
    C.166.9
    D.191.1

    答案：D
    解析：
    根据《砌体结构设计规范》（GB 50003—2011）第5.2.4条规定，已知局部受压面积为：Al=1.2bh=1.2×240×400=115200mm2；砌体局部抗压强度提高系数为：γ=1.5；梁端底面压应力图形的完整系数为：η=0.7；又f=1.58，则局部受压承载力为：
    ηγfAl=0.7×1.5×1.58×115200=191117N=191.1kN。由此可知，D项数值最为接近。

  • 第16题：

    某一间支梁，截面尺寸200mm×400mm，净跨度L0=8m，上面承受均布荷载为1200kN/m，计算最大弯矩及支座反力？梁的支座反力为（）kN。

    • A、1002
    • B、1005
    • C、1008
    • D、1012

    正确答案:C

  • 第17题：

    截面为300mm×500mm的钢筋混凝土梁，净跨度为L0=6m，承受均面荷载500kN/㎡支撑在370mm厚的砖墙上，按满压墙计算，计算砖墙的局部受压应力。已知L=1.05l0，梁的计算跨度L为（）m。

    • A、6.3
    • B、6.4
    • C、6.5
    • D、6.8

    正确答案:A

  • 第18题：

    某一间支梁，截面尺寸200mm×400mm，净跨度L0=8m，上面承受均布荷载为1200kN/m，计算最大弯矩及支座反力？梁端支承在截面尺寸为490mm×490mm的砖柱上，砖柱高度为3m，已知u3=1.85，砖柱的高厚比为（）。

    • A、11.02
    • B、11.33
    • C、11.54
    • D、11.62

    正确答案:B

  • 第19题：

    截面为300mm×500mm的钢筋混凝土梁，净跨度为L0=6m，承受均面荷载500kN/㎡支撑在370mm厚的砖墙上，按满压墙计算，计算砖墙的局部受压应力。砖墙的局部受压力为（）Mpa。

    • A、4.02
    • B、4.26
    • C、4.38
    • D、4.53

    正确答案:B

  • 第20题：

    翼缘上承受均布荷载的梁，是否需要计算局部压应力？


    正确答案: 《钢规》4.1.3条指出，当梁上翼缘受有沿腹板平面作用的集中荷载，且该荷载处又未设置支承加劲肋时，才计算腹板计算高度上边缘的局部压应力。另外对支座处不设置支承加劲肋的情况也要计算，但ψ=1.0。也就是说，计算局部压应力的前提是某截面处承受集中荷载且未设置支承加劲肋。陈绍蕃《钢结构基础》（中国建筑工业出版社，2003年）第62页明确指出，对于翼缘上承受均布荷载的梁，因腹板上边缘的局部压应力不大，不需要进行局部压应力的验算。

  • 第21题：

    在分析垫梁下砌体的局部受压时，可将垫梁视为承受集中荷载的（）。而砌体墙为支承梁的弹性地基


    正确答案:弹性地基梁

  • 第22题：

    多选题
    单向板肋梁楼盖按弹性理论计算时，关于计算简图的支座情况，下面哪些说法是正确的（）。
    A

    计算时对于板和次梁不论其支座是墙还是梁，将其支座均视为铰支座

    B

    对于两边支座为砖墙，中间支座为钢筋混凝土柱的主梁，若时，可将梁视作铰支于柱上的连续梁进行内力分析，否则应按框架横梁计算内力

    C

    当连续梁、板各跨跨度不等，如相邻计算跨度相差不超过20%，可作为等跨计算

    D

    当连续梁板跨度不等时，计算各跨跨中截面弯矩时，应按各自跨度计算；当计算支座截面弯矩时，则应按相邻两跨计算跨度的最大值计算


    正确答案： A,B
    解析： 暂无解析

  • 第23题：

    问答题
    翼缘上承受均布荷载的梁，是否需要计算局部压应力？

    正确答案： 《钢规》4.1.3条指出，当梁上翼缘受有沿腹板平面作用的集中荷载，且该荷载处又未设置支承加劲肋时，才计算腹板计算高度上边缘的局部压应力。另外对支座处不设置支承加劲肋的情况也要计算，但ψ=1.0。也就是说，计算局部压应力的前提是某截面处承受集中荷载且未设置支承加劲肋。陈绍蕃《钢结构基础》（中国建筑工业出版社，2003年）第62页明确指出，对于翼缘上承受均布荷载的梁，因腹板上边缘的局部压应力不大，不需要进行局部压应力的验算。
    解析： 暂无解析

相关内容