3维向量组A：α1，α2，…，αM线性无关的充分必要条件是（）．A、对任意一组不全为0的数k1，k2，…，kM，都有后B、向量组A中任意两个向量都线性无关C、向量组A是正交向量组D、αM不能由线性表示
题目
3维向量组A：α1，α2，…，αM线性无关的充分必要条件是（）．
- A、对任意一组不全为0的数k1，k2，…，kM，都有后
- B、向量组A中任意两个向量都线性无关
- C、向量组A是正交向量组
- D、αM不能由线性表示
相似考题
参考答案和解析
更多“3维向量组A：α1，α2，…，αM线性无关的充分必要条件是（）．”相关问题
-
第1题：
设a1，a2，a3均为3维向量，则对任意常数k,l，向量组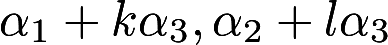
线性无关是向量组a1，a2，a3线性无关的（ ）A.必要非充分条件
B.充分非必要条件
C.充分必要条件
D.既非充分也非必要条件答案：A解析：
-
第2题：
设A为s×n矩阵且A的行向量组线性无关，K为r×s矩阵。证明：B＝KA行无关的充分必要条件是R(K)=r答案：解析：
-
第3题：
设向量组I：α1α2αr…，可由向量组Ⅱβ1,β2,…βs：线性表示，下列命题正确的是( )。A.若向量组I线性无关．则r≤S
B.若向量组I线性相关，则r>s
C.若向量组Ⅱ线性无关，则r≤s
D.若向量组Ⅱ线性相关，则r>s答案：A解析：由于向量组I能由向量组Ⅱ线性表示，所以r(I)≤r(Ⅱ)，即 -
第4题：
单选题设向量β(→)可由向量组α(→)1，α(→)2，…，α(→)m线性表示，但不能由向量组（Ⅰ）：α(→)1，α(→)2，…，α(→)m－1线性表示。记向量组（Ⅱ）：α(→)1，α(→)2，…，α(→)m－1，β(→)，则（ ）。Aαm不能由（Ⅰ）线性表示，也不能由（Ⅱ）线性表示
Bαm不能由（Ⅰ）线性表示，但可由（Ⅱ）线性表示
Cαm可由（Ⅰ）线性表示，也可由（Ⅱ）线性表示
Dαm可由（Ⅰ）线性表示，但不可由（Ⅱ）线性表示
正确答案： B解析：
向量β可由向量组α1，α2，…，αm线性表示，不能由向量组α1，α2，…，αm－1线性表示，则设β＝k1α1＋k2α2＋…＋km－1αm－1＋kmαm，且km≠0，αm＝β/km－k1α1/km－…－km－1αm－1/km，说明αm可由向量组β，α1，α2，…，αm－1，线性表示，不可由向量组α1，α2，…，αm－1线性表示。 -
第5题：
单选题n维向量组α(→)1，α(→)2，…，α(→)s线性无关的充分条件是（ ）。Aα1，α2，…，αs中没有零向量
B向量组的个数不大于维数，即s≤n
Cα1，α2，…，αs中任意两个向量的分量不成比例
D某向量β可由α1，α2，…，αs线性表示，且表示法唯一
正确答案： D解析：
A项，例如α1＝（1，－1，2），α2＝（2，－2，4）都是非零向量，但α1，α2线性相关；
B项，如A项中的例子，α1，α2个数小于维数，但其线性相关；
C项，例如α1＝（1，0，－1），α2＝（0，3，0），α3＝（1，3，－1）中任意两个向量的分量均不成比例，但α1，α2，α3线性相关；
D项，β可由α1，α2，…，αs线性表示，且表示法唯一，即α1，α2，…，αs是α1，α2，…，αs，β的线性极大无关组，故α1，α2，…，αs线性无关。 -
第6题：
单选题设向量组Ⅰ：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组Ⅱ：α(→)1，α(→)2，…， α(→)m，β(→)，其秩为s，则r＝s是向量组Ⅰ与向量组Ⅱ等价的（ ）。A充分非必要条件
B必要非充分条件
C充分必要条件
D既非充分也非必要条件
正确答案： A解析：
两向量组等价的充要条件是它们有相同的秩。 -
第7题：
单选题设A为m×n矩阵，齐次线性方程组AX(→)＝0(→)仅有零解的充分条件是（ ）。AA的列向量组线性无关
BA的列向量组线性相关
CA的行向量组线性无关
DA的行向量组线性相关
正确答案： C解析：
因为AX＝0仅有零解的充分必要条件是A的秩r（A）＝n，所以A的列向量组线性无关是AX＝0仅有零解的充分条件。 -
第8题：
单选题设向量组I：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组II：α(→)1，α(→)2，…，α(→)m，β(→)，其秩为s，则r＝s是向量组I与向量组II等价的（ ）。A充分非必要条件
B必要非充分条件
C充分必要条件
D既非充分也非必要条件
正确答案： C解析：
两向量组等价的充要条件是它们有相同的秩。 -
第9题：
问答题设向量组α(→)1，α(→)2，…，α(→)s的秩为r＞0，证明： （1）α(→)1，α(→)2，…，α(→)s中任意r个线性无关的向量都构成它的一个极大线性无关组； （2）若α(→)1，α(→)2，…，α(→)s中每个向量都可由其中某r个向量线性表示，则这r个向量必为α(→)1，α(→)2，…，α(→)s的一个极大线性无关组。正确答案：
(1)设①:αj1,αj2,…,αjr是α1,α2,…,αs中任意r个线性无关的向量,由于向量组的秩为r,故向量组中任意多于r个向量的向量组必线性相关,所以αj1,αj2,…,αjr,αi(i=1,2,…,s;i≠j1,j2,…,jr)线性相关,从而①为原向量组的极大线性无关组。
(2)设①:αj1,αj2,…,αjr是α1,α2,…,αs中的r个向量,且原向量组中每个向量都可由①线性表示,则原向量组与向量组①等价。等价向量组有相同的秩,原向量组的秩为r,所以向量组①的秩为r。又向量组①只含r个向量,故向量组①线性无关,因此由(1)的结论有①是原向量组的极大线性无关组。解析： 暂无解析 -
第10题：
单选题设n维列向量组α(→)1，α(→)2，…，α(→)m（m＜n）线性无关，则n维列向量组β(→)1，β(→)2，…，β(→)m线性无关的充分必要条件是（ ）。A向量组α1，α2，…，αm可以由β1，β2，…，βm线性表示
B向量组β1，β2，…，βm可以由α1，α2，…，αm线性表示
C向量组α1，α2，…，αm与向量组β1，β2，…，βm等价
D矩阵A＝（α1，α2，…，αm）与矩阵B＝（β1，β2，…，βm）等价
正确答案： D解析：
例如α1＝（1，0，0，0），α2＝（0，1，0，0），β1＝（0，0，1，0），β2＝（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；
D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β1，β2，…，βm线性无关。 -
第11题：
设A为m×n矩阵，则齐次线性方程组Ax＝0有非零解的充分必要条件是（ ）。A、矩阵A的任意两个列向量线性相关
B、矩阵A的任意两个列向量线性无关
C、矩阵A的任一列向量是其余列向量的线性组合
D、矩阵A必有一个列向量是其余列向量的线性组合答案：D解析：
-
第12题：
设α1，α2，α3均为三维向量，则对任意常数k,l，向量组α1+kα3，α2+lα3线性无关是向量组α1，α2,α3线性无关的A.A必要非充分条件
B.充分非必要条件
C.充分必要条件
D.既非充分也非必要条件答案：A解析：
-
第13题：
单选题设n维列向量组α1，α2，…，αm（m＜n）线性无关，则n维列向量组β1，β2，…，βm线性无关的充分必要条件是（ ）.A向量组α1，α2，…，αm可以由β1，β2，…，βm线性表示
B向量组β1，β2，…，βm可以由α1，α2，…，αm线性表示
C向量组α1，…，αm与向量组β1，…，βm等价
D矩阵A=（α1，…，αm）与矩阵B=（β1，…，βm）β）m
正确答案： C解析：
例如α1=（1，0，0，0），α2=（0，1，0，0），β1=（0，0，1，0），β2=（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β1，β2，…，βm线性无关． -
第14题：
单选题向量组α(→)1，α(→)2，…，α(→)s线性无关的充分条件是（ ）。Aα1，α2，…，αs均不为零向量
Bα1，α2，…，αs中任意两个向量的分量不成比例
Cα1，α2，…，αs中任意一个向量均不能由其余s－1个向量线性表示
Dα1，α2，…，αs中有一部分向量线性无关
正确答案： C解析：
A项，均不为零的向量未必线性无关；
B项，例如α1＝（1，0，0）T，α2＝（0，1，0）T，α3＝（1，1，0）T，则其中任意两个向量的分量均不成比例，但向量组α1，α2，α3线性相关；
C项，反证法，如果α1，α2，…，αs线性相关，则至少有一个向量可由其余s－1个向量线性表示，与题设矛盾；
D项，向量组α1，α2，…，αs中部分向量线性无关时，未必全部向量线性无关。 -
第15题：
单选题设A为m×n矩阵，则齐次线性方程组Ax＝0有非零解的充分必要条件是（ ）。[2017年真题]A矩阵A的任意两个列向量线性相关
B矩阵A的任意两个列向量线性无关
C矩阵A的任一列向量是其余列向量的线性组合
D矩阵A必有一个列向量是其余列向量的线性组合
正确答案： D解析：
线性方程组Ax＝0有非零解⇔|A|＝0⇔r（A）＜n，矩阵A的列向量线性相关，所以矩阵A必有一个列向量是其余列向量的线性组合。 -
第16题：
单选题设向量β可以由向量组α1，α2，…，αm线性表示，但不能由向量组（Ⅰ）:α1，α2，…，αm-1线性表示，记向量组（Ⅱ）:α1，α2，…，αm-1，β，则（ ）.Aαm不能由（Ⅰ）线性表示，也不能由（Ⅱ）线性表示
Bαm不能由（Ⅰ）线性表示，但可由（Ⅱ）线性表示
Cαm可以由（Ⅰ）线性表示，也可由（Ⅱ）线性表示
Dαm可由（Ⅰ）线性表示，不可由（Ⅱ）线性表示
正确答案： C解析：
若αm可由向量组（Ⅰ）线性表示，则β也可由向量组（Ⅰ）线性表示，与题设矛盾，故αm不能由（Ⅰ）线性表示；由β可由α1，α2，…，αm线性表示，知存在一组数k1，k2，…，km，使β=k1α1+k2α2+…+kmαm，且km≠0，否则β就能由（Ⅰ）线性表示，所以αm可由向量组（Ⅱ）． -
第17题：
填空题已知向量组（α1，α3），（α1，α3，α4），（α2，α3，）都线性无关，而（α1，α2，α3，α4）线性相关，则向量组（α1，α2，α3，α4）的极大无关组是____.正确答案： (α1,α3,α4)解析：
向量组（α1，α2，α3，α4）线性相关，则其极大线性无关组最多含三个向量，又（α1，α3，α4）线性无关，故知（α1，α3，α4）为其极大线性无关组． -
第18题：
单选题下列说法不正确的是（ ）。As个n维向量α1，α2，…，αs线性无关，则加入k个n维向量β1，β2，…，βk后的向量组仍然线性无关
Bs个n维向量α1，α2，…，αs线性无关，则每个向量增加k维分量后得到的向量组仍然线性无关
Cs个n维向量α1，α2，…，αs线性相关，则加入k个n维向量β1，β2，…，βk后得到的向量组仍然线性相关
Ds个n维向量α1，α2，…，αs线性无关，则减少一个向量后得到的向量组仍然线性无关
正确答案： A解析：
A项，一个线性无关组加入k个线性相关的向量，新的向量组线性相关；
B项，线性无关组的延伸组仍为线性无关组；
C项，线性相关组加入k个向量，无论k个向量是否相关，构成的新的向量组必是线性相关的；
D项，线性无关组中的任意个组合均是无关的。 -
第19题：
单选题设向量组α1，α2，…，αr（Ⅰ）是向量组α1，α2，…，αs（Ⅱ）的部分线性无关组，则（ ）.A（Ⅰ）是（Ⅱ）的极大线性无关组
Br（Ⅰ）=r（Ⅱ）
C当（Ⅰ）中的向量均可由（Ⅱ）线性表示时，r（Ⅰ）=r（Ⅱ）
D当（Ⅱ）中的向量均可由（Ⅰ）线性表示时，r（Ⅰ）=r（Ⅱ）
正确答案： B解析：
题设中只给出向量组（Ⅰ）是（Ⅱ）的部分线性无关组，则不能判定其为（Ⅱ）的极大线性无关组，也没有r（Ⅰ）=r（Ⅱ），若向量组（Ⅱ）可由（Ⅰ）线性表示，则向量组（Ⅰ）和（Ⅱ）等价，即r（Ⅰ）=r（Ⅱ）．