从1，2，3，…，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除，问最多可取几个数（）A、14个B、15个C、16个D、17个

题目

从1，2，3，…，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除，问最多可取几个数（）

  • A、14个
  • B、15个
  • C、16个
  • D、17个
相似考题

1.从1，2，3，……，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于( )。A．0.3024B．0.0302C．0.2561D．0.0285

2.：从1，3，9，27，81，243这六个数中，每次取出若干个数(每次取数，每个数只能取一次)求和，可以得到一个新数，一共有63个数。如果把它们以小到大依次排列起来是：1，3，4，9，10，12，…那么，第60个数是（ ）。A．220B．380C．360D．410

3.：有一列数，第1个数是35，第2个数是25，从第3个数开始，每个数都是它前面两个数的平均数。这列数的第15个数的整数部分是（ ）。A．19B．24C．28D．30

4.从1到9这9个正整数中,每次取出两个数使它们的和大于10,共有________种不同的取法。A．16B．20C．15D．10

参考答案和解析
正确答案:C
更多“从1，2，3，…，30这30个数中，取出若干个数，使其中任意两个”相关问题

  • 第1题：

    关于任意5个不相同的自然数,下列哪个叙述是正确的?()

    A、其中最少有两个数的差是4的倍数

    B、其中最少有两个数的差是5的倍数

    C、其中最少有两个数的差是6的倍数

    D、其中最少有两个数的差是7的倍数


    正确答案：A

  • 第2题：

    从1，2，3，4，…，1000这1000个数中，每次取出两个数，使其和大于1000，共有几种取法?（ ）

    A．250500

    B．250000

    C．249500

    D．200500


    正确答案：B
    A＝1，B可取1000，有1种取法；
    A＝2，B可取1000、999，有2种取法；
    A＝3，B可取1000、999、998，有3种取法；
    A＝500，B可取1000、999、…、501，有500种取法；
    A＝501，B可取1000、999、…、502，有499种取法；
    A＝1000，B可取1，有1种取法。
    所以共有1＋2＋3＋…＋499＋500＋499＋…＋3＋2＋1＝250000(种)不同的取法。
    故本题正确答案为B。

  • 第3题：

    从1，2，3，4，5，6，7这七个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数，其中奇数的个数为

    (A)432 (B)288 (C) 216 (D)108


    正确答案：C

  • 第4题：

    现有20个均不等于7的正整数排成一行，其中，任意连续若干个数的和也不等于7，则这20个数之和的最小值为_______。


    答案：
    解析：
    34。解析：本题考查了一个基本结论：n个正整数排成一行，则必定可以找到其中连续若干个数的和是n的倍数。运用这一结论，则对排成一行的7个正整数而言，必定可以找到连续若干个数的和是7的倍数，如果要求任意连续若干个数的和不等于7，则前述“7的倍数”最小就是l4，此时这7个数是六个1和1个8。对于排成一行的20个正整数而言，任意连续若干个数的和不等于7，它们的和最小的情况是：1，1，1，1，1，1，8，1，1，1，1，1，1，8，1，1，1，1。此时它们的和为34。

  • 第5题：

    从1，3，9，27，8l，243这六个数中，每次取出若干个数(每次取数，每个数只能取一次)求和、可以得到一个新数，一共有63个数。如果把它们以小到大依次排列起来是：1，3，4，9，10，12，…。那么，第60个数是（ ）

    A. 220
    B. 380
    C. 360
    D. 410

    答案：C
    解析：
    一共63个数，第60个也就是倒数第四个，从大往小排列的第四个数。即364-4=360。故答案为C。

  • 第6题：

    从1，2，3，……，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除。问最多可取几个数？（）

    A.14个
    B.15个
    C.16个
    D.17个

    答案：C
    解析：
    任意两个数之积不能被4整除，即两个数分别不能被4整除,那么所取数中最多只能有一个偶数，且该偶数不能为4的倍数;共有15个奇数，所以最多可以取15+1=16个数。故正确答案为C。

  • 第7题：

    从1、2、3、4、5中随机抽取3个数，问这3个数之和至少能被其中一个数整除的概率是多少？

    A. 10%
    B. 30%
    C. 60%
    D. 90%

    答案：D
    解析：
    三个数中只要含有1就能满足，共C4,2=6种，三个数中含有2的话，三个数的和必须是偶数，共C3,2-1=2种，不含1和2只有3、4、5能被3整除，因此共有9种满足的情况，总数为c5,3=10，概率为9/10=90%。

  • 第8题：

    从0，2，4，6中取出3个数字，从1，3，5，7中取出两个数字，共能组成多少个没有重复数字且大于65000的五位数


    答案：
    解析：
    根据约束条件“大于65000的五位数”可知这样的五位数只有 7××××、65×××、67×××三种类型．
    (1)能组成7××××型的五位数的个数是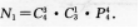

    (2)能组成65×××型的五位数的个数是

    (3)能组成67×××型的五位数的个数是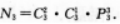

    故所求的五位数的个数为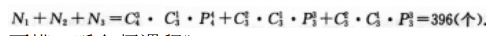

  • 第9题：

    由20×20的小方格组成一个大正方形，从1~9这9个数字中任意选出一个数字填入每个小方格。把其中任意一个田字格图形中的4个数相加，均能得到一个和数。请问所能得到的和数中，至少有（ ）个是相同的。

    A.11
    B.20
    C.33
    D.36

    答案：A
    解析：
    第一步，本题考查最值问题，用极值思维解题。
    第二步，1~9中4个数相加的和数中最小为1+1+1+1=4，最大为9+9+9+9=36，中间每一个都可以取到，则和数的总数为36－4＋1=33（个）。
    第三步，20×20的小方格可以组成（20－1）×（20－1）=19×19=361（个）田字方格。
    第三步，要使相同和数个数尽量少，则每个和数应尽可能的多，最多的情况为个数都相同，则为

    则至少有10＋1=11（个）是相同的。

  • 第10题：

    从任意的自然数中，至少选取（）个数，才能保证一定有两个数的差是5的倍数？

    • A、2
    • B、6
    • C、8
    • D、12

    正确答案:B

  • 第11题：

    单选题
    对于下面两个问题：（1）从5，11，13三个数中每次取出两个数相加，最多可以得出多少个和?（2）从5，11，13三个数中每次取出两个数相减，最多可以得出多少个差?可以得出（　　）．
    A

    问题（1），（2）都属于排列问题

    B

    问题（1），（2）都属于组合问题

    C

    问题（1）属于排列问题，问题（2）属于组合问题

    D

    问题（1）属于组合问题，问题（2）属于排列问题


    正确答案： D
    解析：
    与顺序有关就属于排列，与顺序无关就属于组合．

  • 第12题：

    单选题
    从1，2，3，4，…，1000这1000个数中，每次取出两个数，使其和大于1000，共有几种取法？（　　）
    A

    250500

    B

    250000

    C

    249500

    D

    200500


    正确答案： D
    解析：
    A＝1，B可取1000，有1种取法；A＝2，B可取1000、999，有2种取法；A＝3，B可取1000、999、998，有3种取法；A＝500，B可取1000、999、…、501，有500种取法；A＝501，B可取1000、999、……、502，有499种取法；……A＝1000，B可取1，有1种取法。共有1＋2＋3＋……＋499＋500＋499＋……＋3＋2＋1＝250000种不同的取法。

  • 第13题：

    任意两个数的最小公倍数一定大于这两个数中的任何一个数。()

    此题为判断题(对，错)。


    正确答案：错误

  • 第14题：

    从1，2，3，……，50这五十个数中，取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取多少个数( )。

    A. 21    B. 22C. 23   D. 29


    从0开始，每7个数一组（0——6，7——13，......，42——48，共七组）中，最多可以选4个数（分别是除7余0，1，2，3的数）
    所以，它们之中可以选7*4＝28个数。
    另外：0不包含在其中，要减去1个数；49和50两个数除7的余数分别是0和1，也要计算上，再加2个数。
    故，最多共可取28－1+2＝29个数

  • 第15题：

    1～100，这100个自然数中，最多可以选出多少个数，才能保证任意两个数之和都不能被3整除？（）

    A.33
    B.34
    C.35
    D.36

    答案：C
    解析：
    这100个数可以分成三类：①能被3整除的数，共有33个；②被3除余数是1的数，共有34个；③被3除余数是2的数，共有33个。显然，把第②组的数全选出，再从第①组任选一个数，保证任两个数字之和不能被3整除，即最多可以选出34＋1＝35个，故本题选C。

  • 第16题：

    从1，2，3，……，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于()。

    A:0.3024
    B:0.0302
    C:0.2561
    D:0.0285

    答案：A
    解析：
    该事件的概率=10*9*8*7*6/105=0.3024。

  • 第17题：

    从1,2，3，……，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整 除。问最多可取几个数？

    A.14 个
    B.15 个
    C.16 个
    D.17 个

    答案：C
    解析：
    最多取出所有15个奇数后再任取一个偶数能满足任意两个数的积不能被4整除，所以 最多可取16个数。

  • 第18题：

    从1、3、9、27、81、243这六个数中，每次取出若干个数(每次取数，每个数只能取一次)求和，可以得到一个新数，一共有63个数。如果把它们以小到大依次排列起来是：
    1，3，4，9，10，12，…。那么，第60个数是（　　）。

    A.363
    B.361
    C.360
    D.355

    答案：C
    解析：
    由题目可知，第63个数是364(即6个数之和)，第62个数是364-1=363，第61个数是364-3=361，第60个数是364-1-3=360。

  • 第19题：

    从1、2、3、…、n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为多少？( )

    A.106
    B.107
    C.108
    D.109

    答案：C
    解析：
    根据两数之差不能为13，构造(1、14、27、40、…)、(2、15、28、41、…)、(3、16、29、42…)、…、(13、26、39、…)。显然每个括号中均不能取连续的两个数，现要求任取57个数必有两数差为13时，n的最大值，那考虑取57个可能没有两数之差为13时，凡的最小值，显然每组数中取第1、3、5、7、…个数可使n最小，相当于每26个数取前13个数，那么要取57个数，57÷13-4……5，n最小为26×4+5=109.即n为109时就能满足取57个数且可能没有两数之差为13的情况，当n为108时，必然有两个数之差为13，所以n的最大值为108，

  • 第20题：

    从1．2．3．4．5．6．7．8．9这九个数字中，随机取出一个数字，这个数字是奇数的概率是（）


    答案：B
    解析：

  • 第21题：

    从1、2、3、4、5这五个数字中等可能地、有放回地接连抽取两个数字，则这两个数字不相同的概率为()



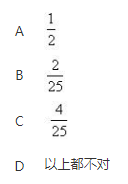    答案：D
    解析：

  • 第22题：

    从1，2，3，…，30这30个数中，取出若干个数，使其中任意两个数的积都不能被4整除，问最多可取几个数（）

    • A、14个
    • B、15个
    • C、16个
    • D、17个

    正确答案:C

  • 第23题：

    单选题
    在1，2，3，…，40中，至少要取出几个数，才能保证取出的数中一定有一个数能被4整除？（）
    A

    3

    B

    4

    C

    21

    D

    31


    正确答案： D
    解析： 1，2，3，…，40中，能被4整除的有10个，因此最少要取出40-10+1=31个才能满足题干要求，选D。

  • 第24题：

    单选题
    有4个不同的自然数，他们当中任意两数的和是2的倍数，任意3个数的和是3的倍数，为了使这4个数的和尽可能小，则这4个数的和为（）
    A

    40

    B

    42

    C

    46

    D

    51


    正确答案： D
    解析： 暂无解析

相关内容