在环保知识竞赛中，男选手的平均得分为80分，女选手的平均得分为65分，全部选手的平均得分为72分。已知全部选手人数在35到50之间，则全部选手人数为（）。A、48B、45C、43D、40

假设B是第二名（或并列第一名），那么A和B得分都比第三名E的96分多，至少各得97分。这样C最多得95X3-2X97 = 91(分)，矛盾。因此，B不可能是第二名。同理，C不可能是第二名。只有D是第二名。
从A、B、C的平均分是95，B、C、D的平均分是94分，得知A比D多1X 3=3(分)，又知A、D的得分都大于96，只有A得100分，D得97分。

题干为平均分计算问题，可利用十字交叉思想快速求解。根据十字交叉法，可列式为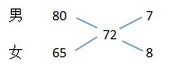：可以得出，男女选手人数之比为，则男女选手总人数应为15的倍数，查看选项，只有B项符合。

故正确答案为B。

解法一：第一步，题目难度较大，无从入手，考虑使用代入排除法解题，代入验证时采用就简代入原则，优先从D选项10开始代入。第二步，若参加比赛的男选手为10人，则参加比赛的女选手为1人，共11人。每场比赛无论是分出胜负还是平局，均共得2分，11人参加循环赛共进行＝55场比赛，得分总数应该为55×2＝110分，男选手得分是女选手的4.5倍，则女选手共得110÷5.5＝20分。1名女选手共参加10场比赛，如果都获胜恰好得20分，满足题意。因此，选择D选项。解法二：设女选手有x人，则男选手有10x人，共有选手11x人。进行循环赛共有



场，每场比赛无论是分出胜负还是平局，均共得2分，因此循环赛总分数为（



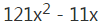
）分。男生所得分数是女生的4.5倍，则女生所得分数为



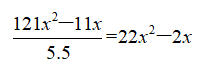
分。一个女生共进行11x－1场比赛，最多得22x－2分，则22x2－2x≤22x－2，解不等式得x≤1，则最多有1名女选手，10名男选手。因此，选择D选项。

第一步，本题考查不定方程问题，用代入排除法解不定方程。
第二步，设获得一等奖的有x位选手、获得二等奖的有y位选手、获得三等奖的有z位选手。根据共10位选手参赛和总分为61分，可列不定方程组：x+y+z=10①，9x+5y+2z=61②，②－①×5可得：4x－3z＝11。
第三步，问该队最多有几位选手获得一等奖，最值代入，优先代入D选项，x＝6，z无整数解，排除；代入C选项，若x＝5，z＝3，y＝2，满足题意。

解题指导： 设这组试卷x份。 90x-97=87x-73 3x=24 x=8。故答案为A。

第一步，本题考查平均数问题。
第二步，根据“甲、乙平均分为85分”，可得总分为85×2=170（分）。设乙得分为x，那么甲得分为x+10，由题意有x+x+10=170，解得x=80。
因此，选择C选项。