方程y2=2px（p＞0）是抛物线标准方程（SIEMENS系统）。

题目

方程y2=2px（p＞0）是抛物线标准方程（SIEMENS系统）。

相似考题

1.若 Normal 0 7.8 磅 0 2 false false false EN-US ZH-CN X-NONE MicrosoftInternetExplorer4 y1·y2为二阶线性常系数微分方程y〞+p1y＇+p2y=0的两个特解，则C1y1+C2y2（）.A.为所给方程的解，但不是通解B.为所给方程的解，但不一定是通解C.为所给方程的通解D.不为所给方程的解

2.抛物线y2=3x的准线方程为 （ ）A.AB.BC.CD.D

3.若y1（x）是线性非齐次方程y '+ p（x）= Q（x）的解，y1（x）是对应的齐次方程y'+p（x）y=0的解，则下列函数中哪一个是y '+ p（x）y= Q（x）的解？ A. y=cy1（x）+y2（x） B. y=y1（x）+c2y2（x） C. y=c[y1 （x）+y2（x）] D.y=c1y（x）-y2（x）

4.抛物线y2=-4x的准线方程为 （ ）A.x=-1B.x=1C.y=1D.Y=-l

更多“方程y2=2px（p＞0）是抛物线标准方程（SIEMENS系统）”相关问题

  • 第1题：

    已知双曲线C：x2/a2-y2/b2=1(a>0，b>0)的一个焦点是抛物线y2=8x的焦点，且双曲线C的离心率为2，那么双曲线C的方程为_______。


    答案：
    解析：

  • 第2题：

    在空间直角坐标系中方程y2=x表示的是（）

    A.抛物线
    B.柱面
    C.椭球面
    D.平面

    答案：B
    解析：
    空间中曲线方程应为方程组，故A不正确；三元一次方程表示空间平面，故D不正确；空间中，缺少一维坐标的方程均表示柱面，可知应选B．

  • 第3题：

    设抛物线y2=2px(p>0)焦点为F，点A坐标为(0，2)，若线段FA的中点B在抛物线上，则B到该抛物线准线距离为__________。


    答案：
    解析：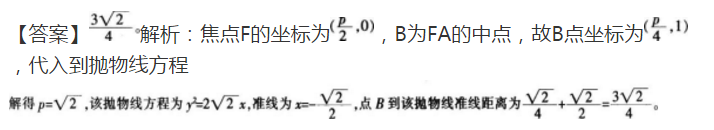

  • 第4题：

    已知抛物线y2=2px(p>0)，过定点(p，0)作两条互相垂直的直线l1、l2，l1与抛物线交于


    答案：
    解析：
    (pk2+P，-pk)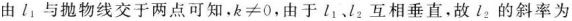

  • 第5题：

    曲线方程y2=2px所描述的是（）。

    • A、摆线
    • B、渐开线
    • C、双曲线
    • D、抛物线

    正确答案:D

  • 第6题：

    下列微分方程是线性微分方程的是（）。

    • A、x（y’）2+y=ex
    • B、xy"+xy’+y=cosx
    • C、y3y"+y’+2y=0
    • D、y"+2y"+y2=0

    正确答案:B

  • 第7题：

    方程 y2 = 2px（p＞0）是抛物线标准方程（SIEMENS系统）。


    正确答案:正确

  • 第8题：

    椭圆参数方程式为X=a*Cosθ；Y=b*Sinθ（SIEMENS系统）。


    正确答案:正确

  • 第9题：

    抛物线标准方程的性质有哪些？


    正确答案: 1.对称性；
    2.顶点在原点；
    3.交点在对称轴；
    4.光束放在焦点通过抛物面反射后，成一束平行于对称轴的光线。

  • 第10题：

    单选题
    若y2（X）是线性非齐次方程y＇+p（x）y-q（x）的解，y1（x）是对应的齐次方程y＇+p（x）y=0的解，则下列函数也是y＇+p（x）y=g（x）的解的是（）。
    A

    y=Cy1（x）+y2（x）

    B

    y=y1（x）+Cy2（x）

    C

    y=C［y1（x）+y2（x）]

    D

    y=Cy1（x）-y2（x）


    正确答案： C
    解析： 暂无解析

  • 第11题：

    填空题
    设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程____的解。

    正确答案： y′+P(x)y=f1(x)+f2(x)
    解析：
    根据题意可知，y1′＋P（x）y1＝f1（x），y2′＋P（x）y2＝f2（x）。两式相加得（y1′＋y2′）＋P（x）（y1＋y2）＝f1（x）＋f2（x）。则可发现y＝y1＋y2是方程y′＋P（x）y＝f1（x）＋f2（x）的解。

  • 第12题：

    单选题
    若y2（x）是线性非齐次方程y′+P（z）y=Q（x）的解，y1（x）是对应的齐次方程y′+P（x）y=0的解，则下列函数中哪一个是y′+P（z）y=Q（x）的解？（）
    A

    y=cy1（x）+y2（x）

    B

    y=y1（x）+c2y2（x）

    C

    y=c[y1（x）+y2（x）]

    D

    y=c1y（x）-y2（x）


    正确答案： D
    解析： 暂无解析

  • 第13题：

    过抛物线y2=4x的焦点，作直线与此抛物线相交于两点P和Q，那么线段PQ中点的轨迹方程是（　　）．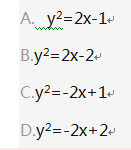


    答案：B
    解析：
    (筛选法)由已知可知轨迹曲线经过点(1，0)，开口向右，由此排除答案A、C、D，所以选B.

  • 第14题：

    已知M是抛物线y2=2px(p>0)上的点，F是抛物线的焦点，∠FOM=45o，|MF|=2。
    (1)求抛物线的方程式；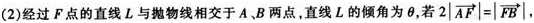




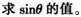
    答案：
    解析：


  • 第15题：

    过抛物线y2=4x的焦点，倾斜角为45°的直线方程为_______。


    答案：
    解析：
    【答案】x-y-1=0。解析：抛物线y2=4x的焦点为(1，0)，倾斜角为45°的直线斜率为1，则直线方程为x-y-1=0。

  • 第16题：

    抛物线公式为y2=2px。


    正确答案:错误

  • 第17题：

    简单可压缩系统状态方程式的基本形式为（）。

    • A、F（p，V，t）=0
    • B、P=f（v）
    • C、方程组p=f（T）和T=g（v）
    • D、f（p，v，T）=0

    正确答案:D

  • 第18题：

    当悬挂点不等高时，用下列哪种方程计算使得导线最大弧垂不在档距中央（）

    • A、平抛物线方程
    • B、斜抛物线方程
    • C、悬链线方程
    • D、悬链线方程级数式

    正确答案:C

  • 第19题：

    下列（）是抛物线方程（FANUC系统、华中系统）。

    • A、X=a+r*cosθ；Y=y=b+r*sinθ
    • B、X=2p*t2；Y=2p*t
    • C、X=a*Cosθ；Y=b*Sinθ
    • D、X2/a2+Y2/b2=1
    • E、Y2=2p*X

    正确答案:B,E

  • 第20题：

    方程y2=2px（p＞0）是抛物线标准方程（FANUC系统、华中系统）。


    正确答案:正确

  • 第21题：

    假定导线的荷载，视为沿直线均匀分布推出的公式称为（）。

    • A、平抛物线方程
    • B、斜抛物线方程
    • C、悬链线方程
    • D、状态方程

    正确答案:A

  • 第22题：

    问答题
    抛物线标准方程的性质有哪些？

    正确答案： 1.对称性；
    2.顶点在原点；
    3.交点在对称轴；
    4.光束放在焦点通过抛物面反射后，成一束平行于对称轴的光线。
    解析： 暂无解析

  • 第23题：

    问答题
    设二阶线性微分方程y″＋P（x）y′＋Q（x）y＝f（x）的三个特解是y1＝x，y2＝ex，y3＝e2x，试求此方程满足条件y（0）＝1，y′（0）＝3的特解。

    正确答案：
    由题意可知,Y1=ex-x、Y2=e2x-x是原方程对应齐次方程的两个线性无关的解[因(ex-x)/(e2x-x)≠常数],故原方程的通解为y=C1(ex-x)+C2(e2x-x)+x,由y(0)=1,y′(0)=3,得C1=-1,C2=2。故所求原方程的特解为y=-(ex-x)+2(e2x-x)+x=2e2x-ex。
    解析： 暂无解析

  • 第24题：

    判断题
    抛物线公式为y2=2px。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容