第52－54题为套题： 假设某损失分布服从二项分布，损失概率P＝002，风险单位的数量为N。 52．当N＝1000时，期望损失为( )。A.0.02B.2C.1000D.条件不足，无法计算

题目

第52－54题为套题： 假设某损失分布服从二项分布，损失概率P＝002，风险单位的数量为N。 52．当N＝1000时，期望损失为( )。

A.0.02

B.2

C.1000

D.条件不足，无法计算

相似考题

1.当风险单位n→∞时,平均损失的标准差会趋于零,预期的损失将会变为没有偏差的必然事件。()此题为判断题(对，错)。

2.第2－4题为套题：假设某损失分布服从二项分布，损失概率P＝0.002，风险单位的数量为N。当N＝1000时，期望损失为()。A.0.02B.2C.1000D.条件不足，无法计算

3.当某现象的发生率π甚小，而样本例数n很大时A、可用泊松分布代替二项分布计算概率B、可用正态分布代替二项分布C、可用t分布代替二项分布D、只能用二项分布E、以上均不对

4.已知随机变量X服从二项分布,且E(X)=2.4,D(X)=1.44,则二项分布的参数n,p的值为()。A、n=4，p=0.6B、n=6，p=0.4C、n=4，p=0.3D、n=24，p=0.1

更多“第52－54题为套题: 假设某损失分布服从二项分布,损失概率P=002,风险单位的数量为N。 52.当N=100 ”相关问题

  • 第1题：

    在假设检验中，如果两个总体的分布没有重叠，那么

    A、若n增大，P（x）与P（n-x）的差减少

    B、若n增大，二项分布图形接近正态分布

    C、若接近0.5，二项分布图形接 近正态分布

    D、若nπ＞5，二项分布图形接近正态分布

    E、二 项分布中的n很大，π很小， 则可用泊松分布近似 二 项 分 布


    参考答案：D

  • 第2题：

    对于X服从二项分布B(n,p),则E(X)=p。()


    正确答案:错

  • 第3题：

    假设某损失分布服从二项分布,损失概率P=0.002,风险单位的数量为N。当N=1000时,期望损失为( )。

    假设某损失分布服从二项分布，损失概率P=0.002，风险单位的数量为N。

    1.当N=1000时，期望损失为( )。

    A.0.02

    B.2

    C.1000

    D.条件不足，无法计算


    参考答案：B

  • 第4题：

    已知随机变量X服从二项分布，且E(X)=2.4，D(X)=1.44，则二项分布的参数n,p分别是：

    A. n=4,p=0. 6
    B. n=6,p=0.4
    C. n=8,p=0.3
    D.n=24,p=0. 1

    答案：B
    解析：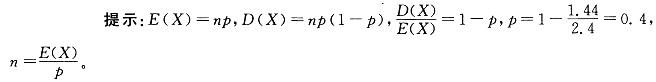

  • 第5题：

    有关二项分布正确的是（）

    • A、二项分布的变量是连续型变量
    • B、Excel中NORMDIST（）函数计算二项分布的概率
    • C、二项分布由n和p两个参数决定
    • D、二项分布中平均值为μ=n/p

    正确答案:C

  • 第6题：

    当知道n时，服从Poisson分布的资料也可用二项分布来处理。


    正确答案:正确

  • 第7题：

    若X服从二项分布b（k；n，p），则EX=npq


    正确答案:错误

  • 第8题：

    已知随机变量X服从二项分布，且EX=2.4，DX=1.44，则二项分布的参数n，p的值为（）。

    • A、n=4，p=0.6
    • B、n=6，p=0.4
    • C、n=8，p=0.3
    • D、n=24，p=0.1

    正确答案:B

  • 第9题：

    若随机变量X服从参数为n和p的二项分布，则它的数学期望为（），方差是（）


    正确答案:np；npq

  • 第10题：

    若一批产品数量无限大，在产品总体不合格品率为P下，从总体随机抽取一个容量为n的样本，则其中含有x个不合格品的概率服从（）。

    • A、正态分布
    • B、泊松分布
    • C、超几何分布
    • D、二项分布

    正确答案:D

  • 第11题：

    单选题
    把一颗均匀骰子掷了6次，假定各次出现的点数相互不影响，随机变量X表示出现6点的次数，则X服从（）．
    A

    参数n=6，p=1/2的二项分布

    B

    参数n=1，p=1/6的二项分布

    C

    参数，n=6，p=1/6的二项分布

    D

    非二项分布


    正确答案： B
    解析： 每掷一次骰子可以看成做一次伯努利试验，把"出现6点"看做"成功"，把"不出现6点"看做"失败"．独立地掷6次骰子相当于重复独立地做6次伯努利试验，且一次伯努利试验后出现成功的概率p=1/6，故选(C)． 如果把"出现6点"看做"失败"，把"不出现6点"看做"成功"，那么p=5/4，因此，也可以认为随机变量X服从参数n=6，p=5/6的二项分布．

  • 第12题：

    多选题
    下列关于几种概率分布之间的关系的陈述中，正确的有（）。
    A

    二点分布（0－1分布）是二项分布的特例

    B

    当n很大而p又很小时，二项分布可用参数λ＝np的泊松分布近似

    C

    当N很大而M/N很小是，超几何分布趋于二项分布

    D

    当n＞30时，不管p大小，二项分布的概率都可用正态分布来近似计算

    E

    当n无限增大时，二项分布趋近于正态分布


    正确答案： D,A
    解析： 暂无解析

  • 第13题：

    在某事件的每次实验中，设成功的概率为P，则失败的概率为Q（＝1-P），在n次实验中，该事件成功k次的概率为Pn（k）＝CnkPk（1-P）n-k，问成功次数k服从什么分布

    A、泊松分布

    B、二项分布

    C、正态分布

    D、F分布

    E、超儿何分布


    参考答案：B

  • 第14题：

    第 52－54 题为套题： 假设某损失分布服从二项分布，损失概率P＝002，风险单位的数量为N。 52．当N＝1000 时，期望损失为( )。

    A.0．02

    B.2

    C.1000

    D.条件不足，无法计算


    参考答案：B
    P116，倒12－5行

  • 第15题：

    已知随机变量X服从二项分布，且E(X)=2.4，D(X)=1.44，则二项分布的参数n、p分别为( )。

    A.n=4，p=06
    B.n=24，p=144
    C.n=6，p=04
    D.n=6，p=06

    答案：C
    解析：
    E(X)=np，D(X)=np(1-p)

  • 第16题：

    在假设检验中，如果两个总体的分布没有重叠，那么（）

    • A、若n增大，P（x）与P（n-x）的差减少
    • B、若n增大，二项分布图形接近正态分布
    • C、若接近0.5，二项分布图形接近正态分布
    • D、若nπ＞5，二项分布图形接近正态分布
    • E、二项分布中的n很大，π很小，则可用泊松分布近似二项分布

    正确答案:D

  • 第17题：

    若人群中某疾病发生的阳性人数X服从二项分布，从该人群中随机抽取n个人，则阳性人数X不小于k人的概率为（）

    • A、P（X≥k）
    • B、P（X≥k+1）
    • C、P（X≤k）
    • D、P（X≤k-1）

    正确答案:A

  • 第18题：

    把一颗均匀骰子掷了6次，假定各次出现的点数相互不影响，随机变量X表示出现6点的次数，则X服从（）．

    • A、参数n=6，p=1/2的二项分布
    • B、参数n=1，p=1/6的二项分布
    • C、参数，n=6，p=1/6的二项分布
    • D、非二项分布

    正确答案:C

  • 第19题：

    设随机变量X服从以n，p为参数的二项分布，且EX=15，DX=10，则n=（）。


    正确答案:45

  • 第20题：

    设X服从二项分布，EX=2.4，DX=1.44，则二项分布的参数为（）.

    • A、n=6，p=0.4
    • B、n=6，p=0.1
    • C、n=8，p=0.3
    • D、n=24，p=0.1

    正确答案:A

  • 第21题：

    二项分布B（n，p）的数学期望为（）

    • A、n（1-n）p
    • B、np（1-p）
    • C、np
    • D、n（1-p）

    正确答案:C

  • 第22题：

    单选题
    若某人群某疾病发生的阳性数X服从二项分布，则从该人群中随机抽出n个人，阳性数X不少于k人的概率为（）。
    A

    P（k+1）+P（k+2）+…+P（n）

    B

    P（0）+P（1）+…+P（k）

    C

    P（0）+P（1）+…+P（k+1）

    D

    P（k）+P（k+1）+…+P（n）

    E

    P（1）+P（2）+…+P（k）


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    设某险种的实际损失额有几种可能：25、50、75、100、200、500，发生的概率分别为0.2、0.3、0.2、0.15、0.1、0.05，假设损失次数服从参数为r=10、β=0.3的奇异负二项分布，免赔额为50，则理赔次数的分布为（　　）。
    A

    NB（10，0.3）

    B

    NB（10，0.15）

    C

    B（10，0.3）

    D

    B（10，0.15）

    E

    B（10，0.45）


    正确答案： C
    解析：
    X表示索赔额，则索赔的概率为：
    υ=P（X＞50）=0.2+0.15+0.1+0.05=0.5
    以N*表示免赔额为50时的理赔次数，则其概率母函数为：
    PN*（t）={1-0.3[1+0.5（t-1）-1]}-10=[1-0.15（t-1）]-10
    所以理赔次数服从奇异二项分布，参数分别为10和0.15。

  • 第24题：

    单选题
    在假设检验中，如果两个总体的分布没有重叠，那么（）
    A

    若n增大，P（x）与P（n-x）的差减少

    B

    若n增大，二项分布图形接近正态分布

    C

    若接近0.5，二项分布图形接近正态分布

    D

    若nπ＞5，二项分布图形接近正态分布

    E

    二项分布中的n很大，π很小，则可用泊松分布近似二项分布


    正确答案： A
    解析： 暂无解析

相关内容