两个等价向量组所含向量的个数一定相等.

题目

两个等价向量组所含向量的个数一定相等.

相似考题

1.等价的两个线性无关向量组所含有向量的个数一定相等。()此题为判断题(对，错)。

2.3维向量组A：a1，a2，…，am线性无关的充分必要条件是( ).A.对任意一组不全为0的数k1，k2，…，km，都有k1a1+k2a2+…+kmam≠0 B.向量组A中任意两个向量都线性无关 C.向量组A是正交向量组 D.

3.设矩阵A,B,C均为n阶矩阵，若AB=C，且B可逆，则（ ）A.矩阵C的行向量组与矩阵A的行向量组等价 B.矩阵C的列向量组与矩阵A的列向量组等价 C.矩阵C的行向量组与矩阵B的行向量组等价 D.矩阵C的行向量组与矩阵B的列向量组等价

4.设矩阵A与B等价，则必有（ ） A.A的行向量与B的行向量等价 B.A的行向量与B的行向量等价 C.Ax=0与Bx=0同解 D.Ax=0与Bx=0的基础解系中向量个数相同

更多“两个等价向量组所含向量的个数一定相等.”相关问题

  • 第1题：

    设A，B，C均为n阶矩阵，若AB=C，且B可逆，则



    A.A矩阵C的行向量组与矩阵A的行向量组等价
    B.矩阵C的列向量组与矩阵A的列向量组等价
    C.矩阵C的行向量组与矩阵B的行向量组等价
    D.矩阵C的列向量组与矩阵B的列向量组等价

    答案：B
    解析：
    对矩阵A，C分别按列分块，记A=(α1，α2，…，αn)，C=(γ，γ，…，γ).　　由AB=C有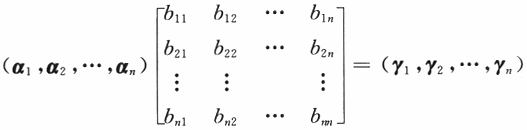

    　　可见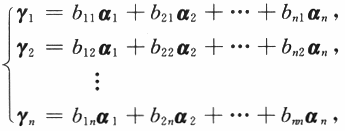

    即C的列向量组可以由A的列向量组线性表出.
    　　因为B可逆，有CB^-1=A.类似地，A的列向量组也可由C的列向量组线性表出，因此选(B).

  • 第2题：

    3维向量组A：α1，α2，…，αM线性无关的充分必要条件是（）．

    • A、对任意一组不全为0的数k1，k2，…，kM，都有后
    • B、向量组A中任意两个向量都线性无关
    • C、向量组A是正交向量组
    • D、αM不能由线性表示

    正确答案:A

  • 第3题：

    单选题
    n维向量组α(→)1，α(→)2，…，α(→)s线性无关的充分条件是（　　）。
    A

    α(→)1，α(→)2，…，α(→)s中没有零向量

    B

    向量组的个数不大于维数，即s≤n

    C

    α(→)1，α(→)2，…，α(→)s中任意两个向量的分量不成比例

    D

    某向量β(→)可由α(→)1，α(→)2，…，α(→)s线性表示，且表示法唯一


    正确答案： D
    解析：
    A项，例如α(→)1＝（1，－1，2），α(→)2＝（2，－2，4）都是非零向量，但α(→)1，α(→)2线性相关；
    B项，如A项中的例子，α(→)1，α(→)2个数小于维数，但其线性相关；
    C项，例如α(→)1＝（1，0，－1），α(→)2＝（0，3，0），α(→)3＝（1，3，－1）中任意两个向量的分量均不成比例，但α(→)1，α(→)2，α(→)3线性相关；
    D项，β(→)可由α(→)1，α(→)2，…，α(→)s线性表示，且表示法唯一，即α(→)1，α(→)2，…，α(→)s是α(→)1，α(→)2，…，α(→)s，β(→)的线性极大无关组，故α(→)1，α(→)2，…，α(→)s线性无关。

  • 第4题：

    单选题
    设向量组α(→)1，α(→)2，…，α(→)s的秩为r，则（　　）。
    A

    必定r＜s

    B

    向量组中任意个数小于r的部分组线性无关

    C

    向量组中任意r个向量线性无关

    D

    若s＞r，则向量组中任意r＋l个向量必线性相关


    正确答案： A
    解析：
    A项，r可能与s相等；
    B项，若r＜s，向量组中可以有两个向量成比例；
    C项，当r小于s/2时，r个向量可能相关；
    D项，任意r＋1个向量若不线性相关，则向量组的秩为r＋1，故必相关。

  • 第5题：

    单选题
    设向量组的秩为r，则：（）
    A

    该向量组所含向量的个数必大于r

    B

    该向量级中任何r个向量必线性无关，任何r+1个向量必线性相关

    C

    该向量组中有r个向量线性无关，有r+1个向量线性相关

    D

    该向量组中有r个向量线性无关，任何r+1个向量必线性相关


    正确答案： C
    解析： 暂无解析

  • 第6题：

    单选题
    设n维列向量组α(→)1，α(→)2，…，α(→)m（m＜n）线性无关，则n维列向量组β(→)1，β(→)2，…，β(→)m线性无关的充分必要条件是（　　）。
    A

    向量组α(→)1，α(→)2，…，α(→)m可以由β(→)1，β(→)2，…，β(→)m线性表示

    B

    向量组β(→)1，β(→)2，…，β(→)m可以由α(→)1，α(→)2，…，α(→)m线性表示

    C

    向量组α(→)1，α(→)2，…，α(→)m与向量组β(→)1，β(→)2，…，β(→)m等价

    D

    矩阵A＝（α(→)1，α(→)2，…，α(→)m）与矩阵B＝（β(→)1，β(→)2，…，β(→)m）等价


    正确答案： D
    解析：
    例如α(→)1＝（1，0，0，0），α(→)2＝（0，1，0，0），β(→)1＝（0，0，1，0），β(→)2＝（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；
    D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β(→)1，β(→)2，…，β(→)m线性无关。

  • 第7题：


    A.必定r＜s
    B.向量组中任意个数小于r的部分组线性无关
    C.向量组中任意r个向量线性无关
    D.若s＞r则向量组中任r+l个向量必线性相关

    答案：D
    解析：

  • 第8题：

    单选题
    设n维列向量组α1，α2，…，αm（m＜n）线性无关，则n维列向量组β1，β2，…，βm线性无关的充分必要条件是（　　）.
    A

    向量组α1，α2，…，αm可以由β1，β2，…，βm线性表示

    B

    向量组β1，β2，…，βm可以由α1，α2，…，αm线性表示

    C

    向量组α1，…，αm与向量组β1，…，βm等价

    D

    矩阵A=（α1，…，αm）与矩阵B=（β1，…，βm）β）m


    正确答案： C
    解析：
    例如α1=（1，0，0，0），α2=（0，1，0，0），β1=（0，0，1，0），β2=（0，0，0，1），各自都线性无关，但它们之间不能相互线性表示，也就不可能有等价关系，排除A、B、C项；D项，矩阵A与矩阵B等价，则它们的秩相等，故向量组β1，β2，…，βm线性无关．

  • 第9题：

    单选题
    设向量组Ⅰ：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组Ⅱ：α(→)1，α(→)2，…， α(→)m，β(→)，其秩为s，则r＝s是向量组Ⅰ与向量组Ⅱ等价的（　　）。
    A

    充分非必要条件

    B

    必要非充分条件

    C

    充分必要条件

    D

    既非充分也非必要条件


    正确答案： A
    解析：
    两向量组等价的充要条件是它们有相同的秩。

  • 第10题：

    单选题
    设向量组I：α(→)1，α(→)2，…，α(→)m，其秩为r；向量组II：α(→)1，α(→)2，…，α(→)m，β(→)，其秩为s，则r＝s是向量组I与向量组II等价的（　　）。
    A

    充分非必要条件

    B

    必要非充分条件

    C

    充分必要条件

    D

    既非充分也非必要条件


    正确答案： C
    解析：
    两向量组等价的充要条件是它们有相同的秩。

  • 第11题：

    单选题
    设α(→)1，α(→)2，…，α(→)s和β(→)1，β(→)2，…，β(→)t为两个n维向量组，且秩（α(→)1，α(→)2，…，α(→)s）＝秩（β(→)1，β(→)2，…，β(→)t）＝r，则（　　）。
    A

    此两个向量组等价

    B

    秩（α(→)1，α(→)2，…，α(→)s，β(→)1，β(→)2，…，β(→)t）＝r

    C

    当α(→)1，α(→)2，…，α(→)s可以由β(→)1，β(→)2，…，β(→)t线性表示时，此二向量组等价

    D

    s＝t时，二向量组等价


    正确答案： C
    解析：
    两向量组等价的充要条件是所含向量的个数相等，且能相互线性表示。

  • 第12题：

    单选题
    设A，B为满足AB＝0(→)的任意两个非零矩阵，则必有（　　）。
    A

    A的列向量组线性相关，B的行向量组线性相关

    B

    A的列向量组线性相关，B的列向量组线性相关

    C

    A的行向量组线性相关，B的行向量组线性相关

    D

    A的行向量组线性相关，B的列向量组线性相关


    正确答案： D
    解析：
    设A为m×n矩阵，B为n×s矩阵，由AB＝0(→)知r（A）＋r（B）≤n，又r（A）≥1，r（B）≥1，因此r（A）＜n，r（B）＜n，说明A的列向量组线性相关，B的行向量组线性相关。

相关内容