36、残差平方和SSE表达的是回归模型能够解释Y的变异的部分。回归平方和SSR表达的是Y的变异当中，不能够被回归模型解释的部分。

题目

36、残差平方和SSE表达的是回归模型能够解释Y的变异的部分。回归平方和SSR表达的是Y的变异当中，不能够被回归模型解释的部分。

相似考题

1.逐步回归分析中，当模型中引入新的自变量，则A、总平方和增大，残差平方和减小B、回归平方和增大，残差平方和减小C、回归平方和变化不确定，但残差平方和减小D、回归平方和与残差平方和均增大E、总平方和不变，回归平方和减小

2.二元线性回归模型Y=β0+β1X1+β2X2中，根据调查资料算得调整后的判定系数及R2= 0.9987，则表明( )。A．表明被解释变量的总变差中有99.87%的信息可由解释变量作出解释B．表明被解释变量的总变差中有0.13%的信息未被解释变量作出解释C．模型的拟合优度不高D．总体平方和与回归平方和较远E．总体平方和与残差平方和较近

3.双曲线回归模型的数学表达式是y=axb。()此题为判断题(对，错)。

4.反映由模型中解释变量所解释的那部分离差大小的是（）。A.总体平方和B.回归平方和C.残差平方和

更多“36、残差平方和SSE表达的是回归模型能够解释Y的变异的部分。回归平方和SSR表达的是Y的变异当中，不能够被回归模型解释的部分。”相关问题

  • 第1题：

    关于一元线性回归模型，下列表述错误的是（ ）。


    A.Y=β0+β1X+ε，只涉及一个自变量的回归模型称为一元线性回归模型

    B.因变量Y是自变量X的线性函数加上误差项

    C.β0+β1X反映了由于自变量X的变化而引起的因变量y的线性变化

    D.误差项是个随机变量，表示除线性关系之外的随机因素对Y的影响，能由X和Y的线性关系所解释的Y的变异性

    答案：D
    解析：
    考查一元线性回归模型。

    只涉及一个自变量的一元线性回归模型表示为Y=β0+β1X+ε，因变量Y是自变量X的线性函数（β0+β1X）加上误差项ε；β0+β1X反映了由于自变量X的变化而引起的因变量y的线性变化。误差项ε是个随机变量，表示除线性关系之外的随机因素对Y的影响，它是不能由X和Y的线性关系所解释的Y的变异性。

    ABC选项说法正确，D选项说法错误。

  • 第2题：

    设k为回归模型中的解释变量的个数，n为样本容量，RSS为残差平方和，ESS为回归平方和。则对其总体回归模型进行方程显著性检验时构造的F统计量为（ ）。



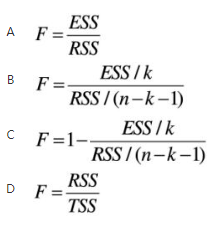    答案：B
    解析：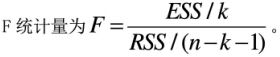

  • 第3题：

    下列关于回归平方和的说法，正确的有（ ）
    Ⅰ.总的变差平方和与残差平方和之差
    Ⅱ.无法用回归直线解释的离差平方和
    Ⅲ.是回归值y与均值离差的平方和
    Ⅳ.实际值y与均值离差的平方和

    A、Ⅰ.Ⅱ.Ⅲ
    B、Ⅰ.Ⅱ.Ⅳ
    C、Ⅰ.Ⅲ
    D、Ⅰ.Ⅳ


    答案：C
    解析：
    总的变差平方和(TSS)均可以分解为回归平方和(RSS)和残差平方和(ESS)两部分。其中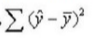

    是回归值y与均值y离差的平方和。和，记为RSS反映了TSS中被y对x回归说明的部分，ESS是TSS中除了y对x回归之外的一切随机因素构成的部分。三个平方和的关系是TSS=RSS+ESS。

  • 第4题：

    下列关于回归平方和的说法，正确的有（ ）。
    Ⅰ.总的变差平方和与残差平方和之差
    Ⅱ.无法用回归直线解释的离差平方和
    Ⅲ.回归值与均值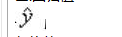离差的平方和
    Ⅳ.实际值y与均值离差的平方和

    A、Ⅰ.Ⅱ
    B、Ⅰ.Ⅱ.Ⅲ
    C、Ⅲ.Ⅳ
    D、Ⅰ.Ⅲ




    答案：D
    解析：
    总的变差平方和(TSS)可以分解为回归平方和(SSR)和残差平方和(ESS)两部分.其中，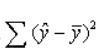

    是回归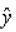值与均值的离差平方和，记为RSS. RSS反映了TSS中被Y对x回归说明的部分.ESS是TSS中除了Y对x回归之外的一切随机因素构成的部分。三个平方和的关系是TSS=RSS+ESS.


  • 第5题：

    残差平方和是指（）。

    • A、随机因素影响所引起的被解释变量的变差
    • B、解释变量变动所引起的被解释变量的变差
    • C、被解释变量的变差中，回归方程不能作出解释的部分
    • D、被解释变量的总离差平方和回归平方之差
    • E、被解释变量的实际值与拟合值的离差平方和

    正确答案:A,C,D,E

  • 第6题：

    计算题：某公司欲了解广告费用x对销售量y的影响，收集了16个地区的数据，并对x、y进行线性回归分析，得到：方程的截距为280，回归系数为1.6，回归平方和SSR=1503000，残差平方和SSE=38000。 要求： （1）写出广告费用x与销售量y之间的线性回归方程。 （2）假如广告费用投入80000元，根据回归方程估计商品的销售量。 （3）计算判定系数R2，并解释它的意义。


    正确答案: （1）销售量y与广告费用x之间的线性回归方程为
    （2）假如广告费用投入80000元，根据回归方程估计商品销售量为128280。
    （3）判定系数R2，它表示回归平方和SSR占平方和SST的比例为97.5%，回归拟合程度很好。

  • 第7题：

    反映由模型中解释变量所解释的那部分离差大小的是（）。

    • A、总离差平方和
    • B、回归平方和
    • C、残差平方和
    • D、可决系数

    正确答案:B

  • 第8题：

    总变动平方和（SST）、回归平方和（SSR）、回归残差平方和（SSE）三者之间的关系可表示为SST=（）。


    正确答案:SSR+SSE

  • 第9题：

    回归方程判定系数的计算公式R^2=SSR/SST=1-SSE/SST，对判定系数描述错误的是（）。

    • A、式中的SSE指残差平方和
    • B、式中的SSR指总离差平方和
    • C、判定系数用来衡量回归方程的扰合优度
    • D、判定系数R^2等于相关系数的平方

    正确答案:B

  • 第10题：

    单选题
    根据某地区2005～2015年农作物种植面积（x）与农作物产值（y），可以建立一元线性回归模型，估计结果得到可决系数R2＝0.9，回归平方和ESS＝90，则回归模型的残差平方和RSS为（　　）。
    A

    10

    B

    100

    C

    90

    D

    81


    正确答案： B
    解析：
    根据公式，R2＝ESS/TSS和TSS＝ESS＋RSS得，TSS＝ESS/R2＝90/0.9＝100，RSS＝TSS－ESS＝100－90＝10。

  • 第11题：

    单选题
    下列关于回归平方和的说法，正确的有（　　）。Ⅰ．总的离差平方和与残差平方和之差Ⅱ．无法用回归直线解释的离差平方和Ⅲ．回归值y(∧)与均值y(＿)的离差平方和Ⅳ．实际值y与均值y(＿)的离差平方和
    A

    Ⅰ、Ⅱ

    B

    Ⅰ、Ⅲ

    C

    Ⅰ、Ⅳ

    D

    Ⅱ、Ⅲ


    正确答案： A
    解析：
    Ⅱ项，回归平方和是可用回归直线解释的离差平方和；Ⅳ项为总离差平方和。

  • 第12题：

    填空题
    总变动平方和（SST）、回归平方和（SSR）、回归残差平方和（SSE）三者之间的关系可表示为SST=（）。

    正确答案： SSR+SSE
    解析： 暂无解析

  • 第13题：

    在k元回归中，n为样本容量，SSE为残差平方和，SSR为回归平方和，则对回归方程线性关系的显著性进行检验时构造的F统计量为（）。



    答案：C
    解析：
    对回归方程线性关系的显著性进行检验的步骤为：



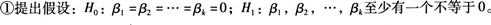
    ②计算检验的统计量F：

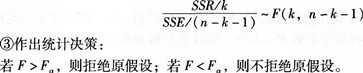
  • 第14题：

    两变量x，y，之间满足方程Y=a+bX，x对y，的回归系数为0.85，已知变量y的变异中有64%可由X的变异解释，那么回归系数6的值为

    A.0.75
    B.0.85
    C.0.80
    D.1.33

    答案：A
    解析：

  • 第15题：

    根据某地区2005-2015年农作物种植面积(X)与农作物产值(Y)，可以建立一元线性回归模型，估计结果得到判定系数R=0.9，回归平方和ESS=90，则回归模型的残差平方和RSS为（ ）。

    A、10
    B、100
    C、90
    D、81

    答案：A
    解析：


    @##

  • 第16题：

    在多元回归模型中，使得（　　）最小的β0，β1…，βk就是所要确定的回归系数。

    A.总体平方和
    B.回归平方和
    C.残差平方和
    D.回归平方和减去残差平方和的差

    答案：C
    解析：
    在多元回归模型中，使得残差平方和最小的β0，β1…，βk就是所要确定的回归系数。

  • 第17题：

    反映由模型中解释变量所解释的那部分离差大小的是（）。

    • A、总体平方和
    • B、回归平方和
    • C、残差平方和

    正确答案:B

  • 第18题：

    在直线回归分析中，Sy.x（直线回归的剩余标准差）反映（）。

    • A、y变量的变异度
    • B、x变量的变异程度
    • C、扣除x影响后y的变异程度
    • D、扣除y的影响后x的变异程度
    • E、回归系数b变异程度

    正确答案:C

  • 第19题：

    总变差平方和SST、回归平方和SSR、回归残差平方和SSE之间的关系是（）。

    • A、SST=SSR+SSE 
    • B、SST=SSR-SSE 
    • C、SSR=SST+SSE 
    • D、SSE=SST+SSR

    正确答案:A

  • 第20题：

    计算题：某公司欲了解广告费用x对销售量y的影响，收集了20个地区的数据，并对x、y进行线性回归分析，得到：方程的截距为364，回归系数为1.42，回归平方和SSR=1602708.6，残差平方和SSE=40158.07。要求： （1）写出广告费用x与销售量y之间的线性回归方程。 （2）假如广告费用投入50000元，根据回归方程估计商品销售量。 （3）计算判定系数R2，并解释它的意义。


    正确答案: （1）销售量y与广告费用x之间的线性回归方程为
    （2）假如广告费用投入50000元，根据回归方程估计商品销售量为71000。
    （3）判定系数R2，，它表示回归平方和SSR占平方和SST的比例为97.6%，回归拟合程度很好。

  • 第21题：

    单选题
    两个变量y与x的回归模型中，通常用R2来刻画回归的效果，则正确的叙述是（）
    A

    R2越小，残差平方和小

    B

    R2越大，残差平方和大

    C

    R2于残差平方和无关

    D

    R2越小，残差平方和大


    正确答案： C
    解析： 暂无解析

  • 第22题：

    单选题
    在回归分析中，下列说法不正确的是（）。
    A

    回归平方和是由于x与y的变化引起的变化部分

    B

    剩余平方和是除了x对y的线性影响之外的其他因素对y的变差的作用

    C

    回归平方和等于y的变差平方和加上剩余平方和

    D

    y的变差平方和可表示为SST=∑（y—y(_)）²


    正确答案： D
    解析：

  • 第23题：

    单选题
    逐步回归分析中，当模型中引入新的自变量，则（　）
    A

    总平方和增大，残差平方和减小

    B

    回归平方和增大，残差平方和减小

    C

    回归平方和变化不确定，但残差平方和减小

    D

    回归平方和与残差平方和均增大

    E

    总平方和不变，回归平方和减小


    正确答案： C
    解析： 暂无解析

  • 第24题：

    单选题
    总变差平方和SST、回归平方和SSR、回归残差平方和SSE之间的关系是（）。
    A

    SST=SSR+SSE 

    B

    SST=SSR-SSE 

    C

    SSR=SST+SSE 

    D

    SSE=SST+SSR


    正确答案： A
    解析： 暂无解析

相关内容