设F（x,y)是随机变量（X,Y)的分布函数, 则P（X＞2,Y＞3)=1+F（2,3).

题目

相似考题

1.设X、Y的联合分布函数是F(x,y),则F(＋∞,y)等于:()A、0;B、1;C、Y的分布函数;D、Y的密度函数。

2.设随机变量X和Y都服从标准正态分布，则A.X+Y服从正态分布. B.X^2+Y^2服从χ^2分布. C.X^2和Y^2都服从χ^2分布. D.X^2/Y^2服从F分布，

3.设随机变量(X,Y)的分布函数为F(x,y),用它表示概率P(-XA.1-F(-a,y) B.1－F(-a,y-0) C.F(+∞,y-0)-F（-a,y-0) D.F(+∞,y)-F(-a,y)

4.设随机变量X,Y相互独立,且X～N,Y～N,则与Z=Y-X同分布的随机变量是().A.X-Y B.X+Y C.X-2Y D.Y-2X

更多“设F（x,y)是随机变量（X,Y)的分布函数, 则P（X＞2,Y＞3)=1+F（2,3).”相关问题

第1题：

设随机变量X,Y相互独立,它们的分布函数为Fx(x),F(y),则Z=min{X,Y}的分布函数为().

答案：C
解析：
FZ(z)=P(Z≤z)=P(min{X,Y}≤z)=1-P(min{X,Y}>z)　　=1-P(X>z,Y>z)=1-P(X>z)P(Y>z)
　　=1-【1-P(X≤z)】【1-P(Y≤z)】=1-【1-FX(z)】【1-FY(z)】，选(C).
第2题：

设二维随机变量(X,Y)的联合密度函数为f(x,y)=
　　(1)求随机变量X,Y的边缘密度函数；
　　(2)判断随机变量X,Y是否相互独立；
　　(3)求随机变量Z=X+2Y的分布函数和密度函数.

答案：
解析：
第3题：

设(X,Y)的联合分布函数为F(x,y)=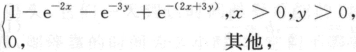则P(max{X,y}>1)=_______.

答案：
解析：
由Fx(x)=F(x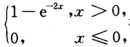，+∞)=得X～E(2)，同理Y～E(3)，且X,Y独立.P(max{X,Y}>1)=P(X>1Y>1)=1-P(X≤1,Y≤1)=1-P(X≤1)P(Y≤1)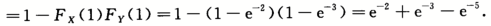
第4题：

设离散型随机变量x的分布函数为

则Y=X^2+1的分布函数为_______.

答案：
解析：
X的分布律为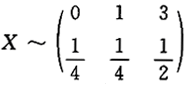，Y的可能取值为1，2，10，　　

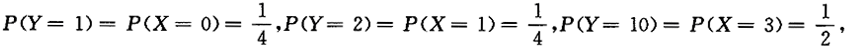
于是Y的分布函数为
　　
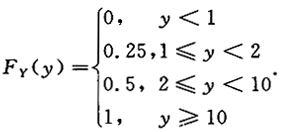
第5题：

设二维随机变量(X,Y)的联合密度函数为f(x,y)=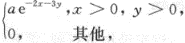则a=_______,P(X>Y)=_______.

答案：
解析：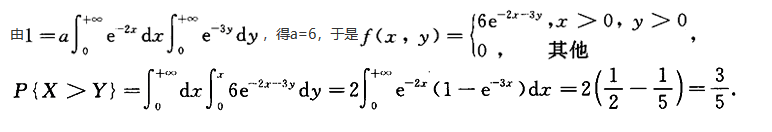
第6题：

设随机变量(X,Y)的联合密度为f(x,y)=.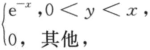则P(X>5｜Y≤3)_______

答案：
解析：
第7题：

设随机变量X，Y独立同分布，且X的分布函数为F(x)，则Z=max{X，Y}的分布函数为

A.AF^2(x)
B.F(x)F(y)
C.1-［1-F(x)］^2
D.［1-F(x)］［1-F(y)］

答案：A
解析：
随机变量Z=max(X，Y)的分布函数Fz(x)应为Fz(x)=P{Z≤x}，由此定义不难推出Fz(x).【求解】故答案应选(A).
【评注】不难验证(B)F(x)F(y)恰是二维随机变量(X，Y)的分布函数.(C)1-［1-F(x)］^2则是随机变量min(X，Y)的分布函数.(D)［1-F(x)］［1-F(y)］本身不是分布函数，因它不满足分布函数的充要条件.
第8题：

设随机变量X的概率密度为令随机变量，
　　(Ⅰ)求Y的分布函数；
　　(Ⅱ)求概率P{X≤Y}.

答案：
解析：
【分析】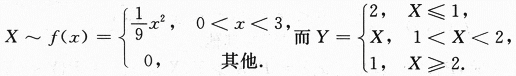
Y是随机变量X的函数，只是这函数是分段表示的，这样得到的Y可能是非连续型，也非离散型，
【解】(Ⅰ)设Y的分布函数为FYy)，显然P{1≤Y≤2}=1，所以，
当y<1时，FY(y)=P{Y≤y)=0；
当1≤y<2时，FY(y)=P{Y≤y}=P{Y<1}+P{Y=1}+P{1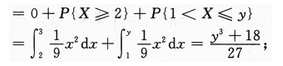
当2≤y时，FY(y)=P{Y≤y}=P{Y≤2}=1.
总之，Y的分布函数为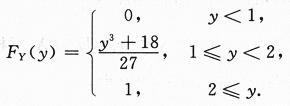

(Ⅱ)因为Y=
第9题：

设X，Y是相互独立的随机变量，X~N（2，σ²），Y~N（-3，σ²），且P{|2X+Y-1|≤8.7654}=0.95，则σ=（）。

正确答案:2
第10题：

设随机变量X与Y相互独立，X~π（2），Y~π（3），则P{X+Y≤1}=（）。

正确答案:6e^-5
第11题：

设两个随机变量X与Y相互独立且同分布，P{X=-1}=P{Y=-1}=1/2，P{X=1}=P{Y=1}=1/2，则下列各式成立的是（）
- A、P{X=Y}=1/2
- B、P{X=Y}=1
- C、P{X+Y=0}=1/4
- D、P{XY=1}=1/4
正确答案:A
第12题：

单选题
设随机变量X的概率密度函数f（x）＝1/[π（1＋x2）]，则Y＝3X的概率密度函数为（　　）。
A
1/[π（1＋y²）]
B
3/[π（9＋y²）]
C
9/[π（9＋y²）]
D
27/[π（9＋y²）]

正确答案： D
解析：
由y＝3x得x＝y/3，故f_Y（y）＝{1/π[1＋（y/3）²]}·（1/3）＝3/[π（9＋y²）]。
第13题：

设随机变量X,Y相互独立,它们的分布函数为Fx(x),FY(y),则Z=max{X,Y)的分布函数为().

答案：B
解析：
FZ(z)=P(Z≤z)=P(max{X,Y}≤z)=P(X≤z,Y≤z)=P(X≤z)P(Y≤z)-FX(z)FY(z)，选(B).
第14题：

设随机变量(X,Y)的联合密度函数为f(x,y)=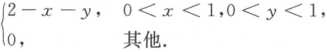(1)求P(X>2Y)；(2)设Z=X+Y,求Z的概率密度函数.

答案：
解析：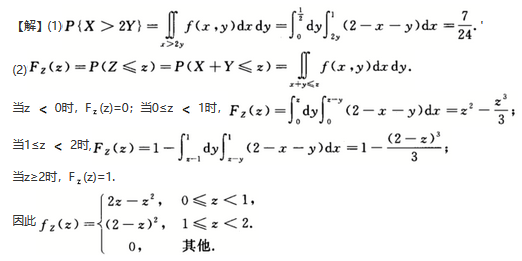
第15题：

设随机变量(X,Y)的联合密度为f(x,y)=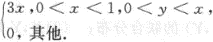求：
　　(1)X,Y的边缘密度；(2)P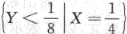

答案：
解析：
第16题：

设随机变量X和Y相互独立,且分布函数为Fx(x)=,Fy(y)=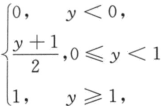,令U=X+Y,则U的分布函数为_______.

答案：
解析：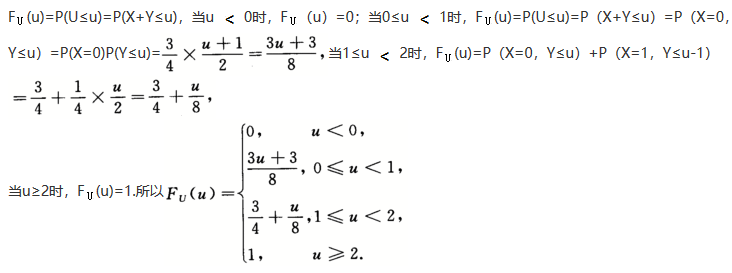
第17题：

设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=,则P（X>1,Y>-2）=_______.

答案：
解析：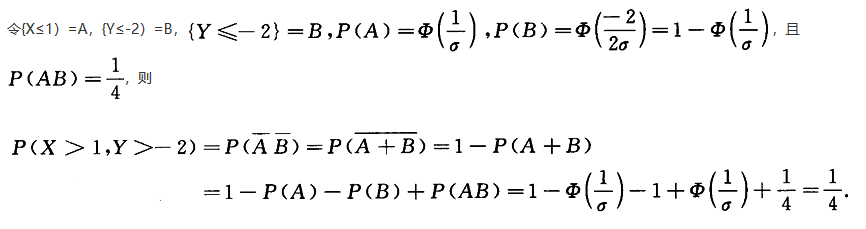
第18题：

设随机变量X,Y相互独立,且X～N(0,4),Y的分布律为Y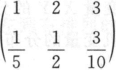～.则P(X-1-2Y≤4)=_______.

答案：1、0.46587
解析：
p(X+2Y≤4)=P(Y=1)P(X≤4-2Y｜Y=1)+P(Y=2)P(X≤4-2Y｜Y=2)+P(Y=3)P(X≤4-2Y｜Y=3)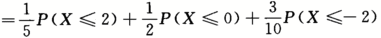
第19题：

设随机变量X的概率分布为P{X=1}=P{X=2}=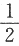，在给定X=i的条件下，随机变量Y服从均匀分布U(0，i)(i=1，2).
　　(Ⅰ)求Y的分布函数FY(y)；
　　(Ⅱ)求EY.

答案：
解析：
第20题：

设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=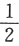.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为

A.A0
B.1
C.2
D.3

答案：D
解析：
第21题：

设二维随机变量（X，Y）在区域D上服从均匀分布，其中D://0≤x≤2，0≤y≤2。记（X，Y）的概率密度为f（x，y），则f（1，1）=（）

正确答案:0.25
第22题：

设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z=max{X，Y}的分布函数为（）
- A、F²（x）
- B、F（x）F（y）
- C、1-[1-F（x）]²
- D、[1-F（x）][1-F（y）]
正确答案:A
第23题：

设随机变量X服从参数为2，p的二项分布，随机变量Y服从参数为3，p的二项分布，若P{X≥1}=5/9，则P{Y≥1}=（）。

正确答案:19/27
第24题：

单选题
设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z＝max{X，Y}的分布函数为（　　）。
A
F²（x）
B
F（x）F（y）
C
1－[1－F（x）]²
D
[1－F（x）][1－F（y）]

正确答案： C
解析：
F_Z（x）＝P{Z≤x}＝P{max（X，Y）≤x}＝P{X≤x，Y≤x}＝P{X≤x}·P{Y≤x}＝F²（x），故应选A。

设F（x,y)是随机变量（X,Y)的分布函数, 则P（X＞2,Y＞3)=1+F（2,3).

题目

相似考题

更多“设F（x,y)是随机变量（X,Y)的分布函数, 则P（X＞2,Y＞3)=1+F（2,3).”相关问题

相关内容