经检验，x和y之间的线性相关关系显著，则可以用建立的回归方程进行y值的预测。

题目

经检验，x和y之间的线性相关关系显著，则可以用建立的回归方程进行y值的预测。

相似考题

1.由回归分析表可知，失业周数与年龄拟合的回归方程方差分析检验结果说明（ ）。A．Y与X之间存在线性相关，但关系不显著B．Y与X之间不存在线性相关关系C．Y与X之间不存在非线性相关关系D．Y与X之间存在显著线性相关关系

2.在求出y随x变化的直线回归方程后，判断回归方程是否显著，需进行显著性检验，如检验的结果是接受零假设，那就意味着A、y与x无直线关系B、y与x有直线关系C、方程求得有问题D、x与y之间毫无关系E、y与x有曲线关系

3.建立变量x、y间的直线回归方程，回归系数的绝对值|b|越大，说明A．回归方程的误差越小B．回归方程的预测效果越好C．回归方程的斜率越大D．x、y间的相关性越密切E．越有理由认为x、y间有因果关系

4.若用最小二乘法以利润率为因变量拟合得到的回归方程为 ，说明（ ）。A．X与Y之间存在着负相关关系B．每人每月销售额X增加一元，则利润率Y就会提高0.002%C．每人每月销售额X增加一元，则利润率Y就会平均提高0.002%D．X与Y之间存在着显著的线性相关关系

更多“经检验，x和y之间的线性相关关系显著，则可以用建立的回归方程进行y值的预测。”相关问题

  • 第1题：

    关于变量销售量y和气温x的相关系数和检验的说法正确的是( )。

    A．相关系数为0.8518

    B．需要查相关系数显著性检验表，α一定时，自由度为8的r值

    C．若α=0.01，相关系数大于相关系数显著性检验值，则可判断出销售量y和气温x之间的线性相关关系对于α=0.01是显著的

    D．若α=0.01，相关系数大于相关系数显著性检验值，则可判断出销售量y和气温x之间的线性相关关系对于α=0.01是不显著的


    正确答案：ABC
    解析：相关系数为：相关系数的显著性检验：自由度：n-2=10-2=8，若α=0.01，r＞ra(n-2)=r0.01(8)=0.765，则可判断出销售量y和气温x之间的线性相关关系对于α=0.01是显著的。

  • 第2题：

    若用最小二乘法以净佣金率为因变量拟合得到的回归方程为Y=-0.852+0.O02X，说明（ ）。

    A．X与Y之间存在着负相关关系

    B．每人每月销售额X增加一元，则净佣金率Y就会提高0.002%

    C．每人每月销售额X增加一元，则净佣金率Y就会平均提高0.002%

    D．X与Y之间存在着显著的线性相关关系


    正确答案：C

  • 第3题：

    若变量x与y之间为完全正相关,则相关系数r=();若x与y之间为完全负相关,则r=();若x与y之间不存在线性相关关系,则r=()。


    答案：1;-1;0

  • 第4题：

    两个变量(x，y)，其观测值为(xi，yi，i=1，2，…，n。若显著性水平为a，简单相关系数为 r，则下列说法正确的有（ ）。

    A.-1≤r≤1

    B.r=0，x、y之间存性相关

    C.r=-1，完全负线性相关

    D.相关系数检验的临界值表示为

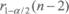
    E.r=0，x、y之间不存性相关


    正确答案：ACDE
    r=0时称两个变量之间线性不相关。

  • 第5题：

    若直线回归方程y=170-2.5x，则变量x和y之间存在着负的相关关系。（ ）


    答案：对
    解析：

  • 第6题：

    对某地区失业人员进行调查，得到有关失业周数、失业者年龄和受教育年限等资料，对此资料进行相关与回归分析后所得的结果如下表所示。
    表1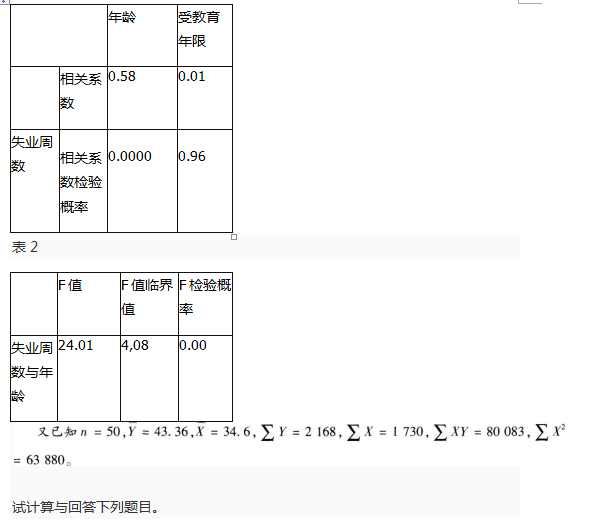

    由回归分析表可知，失业周数与年龄拟合的回归方程方差分析检验结果说明（）。

    A.Y与X之间存在线性相关，但关系不显著
    B.Y与X之间不存在线性相关关系
    C.Y与X之间不存在非线性相关关系
    D.Y与X之间存在显著线性相关关系

    答案：D
    解析：
    在方差分析检验法中，如果统计量的观测值，大于相应的临界值，则可认为F与X的线性相关关系是显著的；否则便认为F与Z的线性相关关系不显著。由表2知，F值=24．01>F临界值=4．08，故F与Y之间存在显著线性相关关系，也可以根据F检验概率P=0．00判断知Y与X之间之间存在显著线性相关关系。

  • 第7题：

    基于大连商品交易所日收盘价数据，对Y1109价格Y(单位:元)和A1109价格*(单位:元)建立一元线性回归方程:Y=-4963.13+3.263*。回归结果显示:可决系数R2=0.922，DW=0.384;对于显著性水平α=0.05，*的T检验的P值为0.000，F检验的P值为0.000.对该回归方程的合理解释是（ ）。

    A. Y和*之间存在显著的线性关系
    B. Y和*之间不存在显著的线性关系
    C. *上涨1元.Y将上涨3.263元
    D. *上涨1元，Y将平均上涨3.263元

    答案：A,D
    解析：
    在显著性水平为0.05的情况下，P值为0.000，远小于0.05，说明检验结果显著，可决系数为0.922，说明建立的一元线性回归模型整体上对样本数据拟合较好。回归系数表示*每变动一单位，平均而言，Y将变动(系数值)个单位。

  • 第8题：

    根据下面资料，回答91-93题
    基于大连商品交易所日收盘价数据，对Y1109价格y(单位：元)和A1109价格X(单位：元)建立一元线性回归方程：Y=-4963．13+3．263X。回归结果显示：R2=0．922，Dw=0．384；对于显著性水平a=0．05，X的t检验的P值为0．000，F检验的P值为0．000。
    据此回答以下三题。
    对该回归方程的合理解释是( )。

    A.Y和X之间存在显著的线性关系
    B.Y和X之问不存在显著的线性关系
    C.X上涨1元，1，将上涨3．263元
    D.X上涨1元，Y将平均上涨3．263元

    答案：A,D
    解析：
    根据R2=0．922，可知所建立的一元线性回归模型整体上对样本数据拟合效果较好，解释变量“A1109的价格X”解释了被解释变量“Y1109的价格]，”变动的92．2％；而在5％的显著性水平下，X的t检验的P值为0．000<0．05，表明X对Y有显著影响。X的回归系数等于3．263，表明A1109的价格X每上涨1元，Y1109的价格Y将平均上涨3．263元。

  • 第9题：

    建立一个回归方程，且b有显著意义，则有一定把握认为x和y之间存在因果关系。


    正确答案:错误

  • 第10题：

    当x与y之间的相关关系可用回归方程y=—2.5—0.14x表达时，表明这两个变量之间存在（）

    • A、正相关
    • B、负相关
    • C、线性相关
    • D、非线性相关
    • E、单相关

    正确答案:B,C,E

  • 第11题：

    如果变量X、Y之间的线性相关系数为-1，则表明变量X、Y之间是非独立的。


    正确答案:正确

  • 第12题：

    判断题
    经检验，x和y之间的线性相关关系显著，可以用建立的回归方程进行y值的预测。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    由回归分析表可知，失业周数与年龄拟合的回归方程方差分析检验结果说明( )。

    A．Y与X之间存性相关，但关系不显著

    B．Y与X之间不存性相关关系

    C．Y与X之间不存在非线性相关关系

    D．Y与X之间存在显著线性相关关系


    正确答案：D
    解析：在方差分析检验法中，如果统计量的观测值F大于相应的临界值，则可认为Y与X的线性相关关系是显著的；否则便认为Y与X的线性相关关系不显著。由表2知， F值=24.01＞F临界值=4.08，故Y与X之间存在显著线性相关关系，也可以根据F检验概率P=0.00判断知Y与X之间存在显著线性相关关系。

  • 第14题：

    根据回归方程y＝a＋bx（ ）。

    A．只能由变量x去预测变量y

    B．只能由变量y去预测变量x

    C．可以由变量x去预测变量y，也可以由变量y去预测变量x

    D．能否相互预测，取决于变量x和变量y之间的因果关系


    正确答案：A
    不能进行逆运算，因x的取值是固定的，而y的值是随机的。

  • 第15题：

    如果变量X、Y之间的线性相关系数为0，则表明变量X、Y之间是独立的。


    正确答案：×
    线性相关系数为0，表明不是线性相关的，也有可能是别的关系，并不简单意味着互相独立。

  • 第16题：

    建立变量X、Y间的直线回归方程，回归系数的绝对值︱b︱越大，说明

    A、回归方程的误差越小

    B、回归方程的预测效果越好

    C、回归直线的斜率越大

    D、X、Y间的相关性越密切

    E、越有理由认为X、Y间有因果关系


    参考答案：C

  • 第17题：

    对某地区失业人员进行调查，得到有关失业周数、失业者年龄和受教育年限等资料，对此资料进行相关与回归分析后所得的结果如表5—1、表5—2所示。





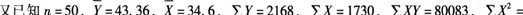
    63880，试计算与回答题目。

    由回归分析表可知，失业周数与年龄拟合的回归方程方差分析检验结果说明（）。

    A.Y与X之间存在线性相关，但关系不显著
    B.Y与X之间不存在线性相关关系
    C.Y与X之间不存在非线性相关关系
    D.Y与X之间存在显著线性相关关系

    答案：D
    解析：
    在方差分析检验法中，如果统计量的观测值F大于相应的临界值，则可认为Y与X的线性相关关系是显著的；否则便认为Y与X的线性相关关系不显著。由表5—2知，F值=24．01>F临界值=4．08，故Y与X之间存在显著线性相关关系，也可以根据F检验概率P=0．00判断知Y与X之间存在显著线性相关关系。

  • 第18题：

    对某地区失业人员进行调查，得到有关失业周数、失业者年龄和受教育年限等资料，对此资料进行相关与回归分析后所得的结果如表5—1、表5—2所示。





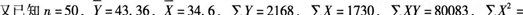
    63880，试计算与回答题目。

    在求解上述回归系数过程中，利用了最小二乘估计准则，这种估计的实质是使（）。


    A.Y与X之间存在线性相关，但关系不显著
    B.Y与X之间不存在线性相关关系
    C.Y与X之间不存在非线性相关关系
    D.Y与X之间存在显著线性相关关系在方差分析检验法中，如果统计量的观测值F大于相应的临界值，则可认为Y与X的线性相关关系是显著的；否则便认为Y与X的线性相关关系不显著。由表5—2知，F值=24．01>F临界值=4．08，故Y与X之间存在显著线性相关关系，也可以根据F检验概率P=0．00判断知Y与X之间存在显著线性相关关系。

    答案：A
    解析：
    最小二乘法估计回归方程中参数的实质是每一个指标实测值与指标理论值的离差

  • 第19题：

    基于大连商品交易所日收盘价数据，对Y1109价格Y(单位:元)和A1109价格*(单位:元)建立一元线性回归方程:Y=-4963.13+3.263*。回归结果显示:可决系数R2=0.922，DW=0.384;对于显著性水平α=0.05，*的T检验的P值为0.000，F检验的P值为0.000.对该回归方程的合理解释是（ ）。

    A、Y和*之间存在显著的线性关系
    B、Y和*之间不存在显著的线性关系
    C、*上涨1元.Y将上涨3.263元
    D、*上涨1元，Y将平均上涨3.263元

    答案：A,D
    解析：
    在显著性水平为0.05的情况下，P值为0.000，远小于0.05，说明检验结果显著，可决系数为0.922，说明建立的一元线性回归模型整体上对样本数据拟合较好。回归系数表示*每变动一单位，平均而言，Y将变动(系数值)个单位。

  • 第20题：

    在一元线性回归分析预测过程中，相关系数r反映变量x和y之间线性相关关系的密切程度，只有r小于某个临界值时，才能认为x与y确实线性相关，也只有这时回归方程才有意义，才可以用于预测计算。


    正确答案:错误

  • 第21题：

    经检验，x和y之间的线性相关关系显著，可以用建立的回归方程进行y值的预测。


    正确答案:正确

  • 第22题：

    若两变量X和y之间的Pearson相关系数大于0.3且小于0.5，则说明（　）。

    • A、X和Y存在低度相关的线性相关关系
    • B、X和Y存在中度相关的线性相关关系
    • C、X和Y完全正线性相关
    • D、X和Y，完全负线性相关

    正确答案:A

  • 第23题：

    多选题
    当x与y之间的相关关系可用回归方程y=—2.5—0.14x表达时，表明这两个变量之间存在（）
    A

    正相关

    B

    负相关

    C

    线性相关

    D

    非线性相关

    E

    单相关


    正确答案： E,B
    解析： 暂无解析

  • 第24题：

    单选题
    若两变量X和y之间的Pearson相关系数大于0.3且小于0.5，则说明（　）。
    A

    X和Y存在低度相关的线性相关关系

    B

    X和Y存在中度相关的线性相关关系

    C

    X和Y完全正线性相关

    D

    X和Y，完全负线性相关


    正确答案： A
    解析： 暂无解析

相关内容