设G是一个有6个结点14条边的连通图,则G为平面图.
题目
设G是一个有6个结点14条边的连通图,则G为平面图.
相似考题
更多“设G是一个有6个结点14条边的连通图,则G为平面图.”相关问题
-
第1题:
若G是一个具有36条边的非连通无向图(不含自回路和多重边),则图G至少有(64)个顶点。
A.11
B.10
C.9
D.8
正确答案:B
解析:根据无向图的定义,有n个顶点的无向图至多有n(n-1)/2条边。试题告诉我们,共有36条边,则n(n-1)/2=36解这个方程可得n=9。但这样求得的9个顶点是连通的,而试题要求是非连通图,所以,再增加一个孤立点,因此至少有10个顶点。 -
第2题:
设有一个无向图G=(V,E)和G′=(V′,E′),如果G′为G的生成树,则下面不正确的说法是(40)。
A.G′为G的子图
B.G′为G的极小连通子图且V′=V
C.G′为G的一个无环子图
D.G′为G的边通分量
正确答案:D
解析:本题考查无向图与其生成树的关系。对于无向图而言,如果无向图G是一个连通图,在对其进行遍历时,一次可以遍历所有顶点,得到的极小连通子图是一棵生成树,树中包含了图的所有顶点,但不一定包含所有的边;如果无向图G是一个非连通图,在对其进行遍历时,得到的是森林,这个森林是由图的连通分量的生成树组成的,森林中也不一定包含图中所有的边。因此,G'不一定为G的边通分量。 -
第3题:
若G是一个具有36条边的非连通无向图(不含自回路和多重边),则图G至少有()个顶点。A.11
B.10
C.9
D.8答案:B解析:要使图的顶点数最少,应该尽量构造一个完全图,具有36条边的无向完全图的顶点数是9,又因为图示非连通的,所以再加一个孤立的顶点即可。所以至少有10个顶点。 -
第4题:
设无向图G有n个顶点m条边,则其邻接表中表结点数是()
- A、n
- B、2n
- C、m
- D、2m
正确答案:D -
第5题:
设无向图G=(V,E)和G’=(V’,E’),如果G’是G的生成树,则下面的说法中错误的是()。
- A、G’为G的子图
- B、G’为G的连通分量
- C、G’为G的极小连通子图且V=V’
- D、G’是G的一个无环子图
正确答案:B -
第6题:
设G为具有N个顶点的无向连通图,则G至少有()条边。
正确答案:N-1 -
第7题:
对于一个图G,若边集E(G)为有向边的集合,则该图为()。
正确答案:有向图 -
第8题:
设无向图G中顶点数为n,则图G至少有()条边,至多有()条边;若G为有向图,则至少有()条边,至多有()条边。
正确答案:0;n(n-1)/2;0;n(n-1) -
第9题:
填空题设G为具有N个顶点的无向连通图,则G至少有()条边。正确答案: N-1解析: 暂无解析 -
第10题:
填空题设无向图G中顶点数为n,则图G至少有()条边,至多有()条边;若G为有向图,则至少有()条边,至多有()条边。正确答案: 0,n(n-1)/2,0,n(n-1)解析: 图的顶点集合是有穷非空的,而边集可以是空集;边数达到最多的图称为完全图,在完全图中,任意两个顶点之间都存在边。 -
第11题:
填空题n个顶点的强连通有向图G,最多有()条边,最少有()边。强连通图即是任何两个顶点之间有路径相通,当所有结点在一个环上时,必定是强连通图。正确答案: n(n-1),n解析: 暂无解析 -
第12题:
单选题设无向图G有n个顶点m条边,则其邻接表中表结点数是()An
B2n
Cm
D2m
正确答案: B解析: 暂无解析 -
第13题:
己知某带权图G的邻接表如下所示,其中表结点的结构为:
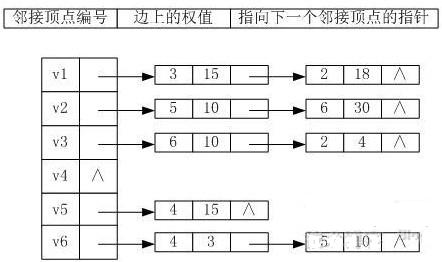
则图G是______。
A.无向图
B.完全图
C.有向图
D.强连通图
正确答案:C
解析:本题考查数据结构基础知识。
完全图是每对顶点之间都恰连有一条边的简单图。n个端点的完全图有n个端点及n(n ? 1) / 2条边。
强连通图(Strongly Connected Graph)是指一个有向图(Directed Graph)中任意两点v1、v2间存在v1到v2的路径(path)及v2到v1的路径的图。
从上面的表结构可以看出,有v1→v3的边,但没有v3→v1的边,显然这不是无向图,也不是完全图和强连通图,只能是有向图。 -
第14题:
设无向图G=(V,E)和G′=(V′,E′),如果G′是G的生成树,则下面的说法中错误的是()。A.G′为G的极小连通子图且V=V′
B.G′是G的一个无环子图
C.G′为G的子图
D.G′为G的连通分量答案:D解析:连通分量是无向图的极大连通子图,其中极大的含义是将依附于连通分量中顶点的所有边都加上,所以,连通分量中可能存在回路。 -
第15题:
已知某带权图G的邻接表如下所示,其中表结点的结构为:
则图G是( )。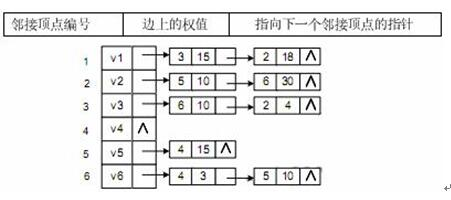 A.无向图
A.无向图
B.完全图
C.有向图
D.强连通图答案:C解析:本题考查数据结构基础知识。
从题中的邻接表中可知,该图的边为、 、 、 、 、 、 、 、 ,如下图所示,显然,这是个有向图。
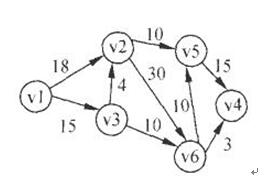
在无向图中,若存在边(vi,vj),则它同时为vj和vi之间的边。在上面的邻接表中,存在边,而不存在 ,因此该图不是无向图。
对于无向图,其边数e和顶点数n的关系为e=n×(n-1)/2。对于有向图,其边数e和顶点数n的关系为e = n×(n-1),因此该图不是完全图。
若有向图为强连通图,则任意两个顶点间要存在路径。在该有向图中,由于顶点v4没有出边,因此,不存在v4到其他顶点的路径,因此该图不是强连通图。 -
第16题:
n个顶点的强连通有向图G,最多有()条边,最少有()边。强连通图即是任何两个顶点之间有路径相通,当所有结点在一个环上时,必定是强连通图。
正确答案:n(n-1),n -
第17题:
设E为程序图G中边的总数;N为程序图中结点的总数,则该程序图的环形复杂度为 ()。
正确答案:E–N+2 -
第18题:
如果G1是一个具有n个顶点的连通无向图,那么G1最多有()条边,G1最少有()条边。如果G2是一个具有n个顶点的强连通有向图,那么G2最多有()条边,G2最少有()条边。
正确答案:n(n-1)/2;n-1;n(n-1);n -
第19题:
对于一个图G,若边集合E(G)为有向边的集合,则称该图为()。
正确答案:有向图 -
第20题:
单选题设无向图G=(V,E)和G’=(V’,E’),如果G’是G的生成树,则下面的说法中错误的是()。AG’为G的子图
BG’为G的连通分量
CG’为G的极小连通子图且V=V’
DG’是G的一个无环子图
正确答案: D解析: 暂无解析 -
第21题:
填空题对于一个图G,若边集合E(G)为有向边的集合,则称该图为()。正确答案: 有向图解析: 暂无解析 -
第22题:
填空题设E为程序图G中边的总数;N为程序图中结点的总数,则该程序图的环形复杂度为 ()。正确答案: E–N+2解析: 暂无解析 -
第23题:
填空题如果G1是一个具有n个顶点的连通无向图,那么G1最多有()条边,G1最少有()条边。如果G2是一个具有n个顶点的强连通有向图,那么G2最多有()条边,G2最少有()条边。正确答案: n(n-1)/2,n-1,n(n-1),n解析: 暂无解析 -
第24题:
填空题对于一个图G,若边集E(G)为有向边的集合,则该图为()。正确答案: 有向图解析: 暂无解析
