某资产组合中有三只股票，相关的信息如表所示，要求计算资产组合的β系数。 某证券资产组合的相关信息
题目
某证券资产组合的相关信息
相似考题
参考答案和解析
A股票比例：（4×200）÷（4×200＋2×100＋10×100）×100%＝40%
B股票比例：（2×100）÷（4×200＋2×100＋10×100）×100%＝10%
C股票比例：（10×100）÷（4×200＋2×100＋10×100）×100%＝50%
然后计算加权平均β系数，即为资产组合的β系数：
βp＝40%×0.7＋10%×1.1＋50%×1.7＝1.24
更多“某资产组合中有三只股票，相关的信息如表所示，要求计算资产组合的β系数。 ”相关问题
-
第1题：
某公司拟进行股票投资，计划购买A、B、C三种股票，并分别设计了甲、乙两种资产组合。已知三种股票的口系数分别为1.5、1.0和0.5，它们在甲种资产组合下的投资比重为50%、30%和20%；乙种资产组合的风险收益率为3.4%。同期市场上所有股票的平均收益率为12%，无风险收益率为8%。
要求：
(1)根据A、B、C股票的β系数，分别评价这三种股票相对于市场投资组合而言的系统风险大大小；
(2)按照资本资产定价模型计算A股票的必要收益率；
(3)计算甲种资产组合的β系数和风险收益率；
(4)计算乙种资产组合的β系数和必要收益率；
(5)比较甲、乙两种资产组合的β系数，并据以评价它们的投资风险大小。
正确答案：
(1)市场组合的β系数为1.0，而β系数是衡量系统风险的，所以，A股票的系统风险高于市场组合的风险；B股票的系统风险等于市场组合的风险；C股票的系统风险低于市场组合的风险。
(2)A股票的必要收益率
＝8%+1.5×(12%－8%)＝14%
(3)甲种资产组合的口系数
＝1.5×50%+1.0×30%+0.5×20%＝1.15
甲种资产组合的风险收益率
＝1.15×(12%－8%)＝4.6%
(4)乙种资产组合的舟系数
＝3.4%/(12%－8%)＝O.85
乙种资产组合的必要收益率
＝8%+3.4%＝11.4%
(5)甲种资产组合的β系数1.15大于乙种资产组合的口系数0.85，说明甲的投资风险大于乙的投资风险。 -
第2题：
已知甲股票的β系数为1.2，证券市场线的斜率为8%，证券市场线的截距为2.4%，资本资产定价模型成立，乙股票收益率与市场组合收益率的协方差为6.3%，市场组合收益率的标准差为30%。
要求：
(1)根据题中条件确定市场风险溢酬；
(2)计算无风险收益率以及甲股票的风险收益率和必要收益率；
(3)计算甲股票的预期收益率；
(4)计算市场平均收益率；
(5)计算乙股票的β系数；
(6)如果资产组合中甲的投资比例为0.4，乙的投资比例为0.6，计算资产组合的β系数以及资产组合的必要收益率；
(7)在第6问中，假设资产组合收益率与市场组合收益率的相关系数为0.8，计算资产组合收益率的标准差；
(8)如果甲股票收益率标准差为18%，乙股票收益率的标准差为10%，资产组合中甲的投资比例为0.3，乙的投资比例为0.7，资产组合收益率的标准差为8.5%，计算甲乙股票收益率的协方差；
(9)根据第8问计算甲乙股票收益率的相关系数；
(10)根据第2问、第3问和第8问，计算甲股票的风险价值系数。
正确答案：(1)证券市场线的斜率=市场风险溢酬
由此可知：市场风险溢酬=8%
(2)证券市场线的截距=无风险收益率
由此可知，无风险收益率=2.4%
甲股票的风险收益率=甲股票的β系数×市场风险溢酬=1.2×8%=9.6%
甲股票的必要收益率=无风险收益率+甲股票的风险收益率=2.4%+9.6%=12%
(3)由于资本资产定价模型成立，所以，甲股票的预期收益率=必要收益率=12%
(4)市场平均收益率=市场组合收益率=无风险收益率+市场风险溢酬=2.4%+8%=10.4%
(5)市场组合收益率的方差=30%×30%=9%
乙股票的β系数=乙股票收益率与市场组合收益率的协方差/市场组合收益率的方差=6.3%/9%=0.7
(6)资产组合的β系数=0.4×1.2+0.6×0.7=0.9
资产组合的必要收益率=2.4%+0.9×8%=9.6%
或：资产组合的必要收益率=0.4×甲股票的必要收益率+0.6 ×乙股票的必要收益率=0.4 × 12%+0.6 ×(2.4%+0.7×8%)=9.6%
(7)资产组合的β系数=资产组合收益率与市场组合收益率的相关系数×资产组合收益率的标准差/市场组合收益率的标准差
即：0.9=0.8×资产组合收益率的标准差/30%
解得：资产组合收益率的标准差=33.75%
(8)资产组合收益率的方差
=0.3×0.3×18%×18%+2×0.3 ×0.7×甲乙股票收益率的协方差+0.7×0.7 × 10%×10%
即：8.5%×8.5%=0.3 × 0.3×18%× 18%+2×0.3×0.7×甲乙股票收益率的协方差+0.7×0.7×10%×10%
0.7225%=0.2916%+0.42 ×甲乙股票收益率的协方差+0.49%
解得：甲乙股票收益率的协方差=-0.14%
(9)甲乙股票收益率的协方差=甲乙股票收益率的相关系数×甲的收益率标准差×乙的收益率标准差=甲乙股票收益率的相关系数×18%×10%=-0.14%
解得：甲乙股票收益率的相关系数=-0.08
(10)甲股票的风险价值系数=甲股票的风险收益率/甲股票收益率的标准离差率=9．6%/甲股票收益率的标准离差率甲股票收益率的标准离差率=甲股票收益的标准差/甲股票的预期收益率=18%/12%=1.5
所以，甲股票的风险价值系数=9.6%/1.5=6.4% -
第3题：
已知甲股票的风险收益率为20%，市场组合的风险收益率为16%，甲股票的必要收益率为25%，假设资本资产定价模型成立，乙股票的届系数为0.8，乙股票收益率与市场组合收益率的协方差为40%，由甲、乙股票构成的资产组合中甲的投资比例为0.6，乙的投资比例为0.4。
要求：
(1)计算甲股票的β系数、无风险收益率；
(2)计算股票价格指数平均收益率；
(3)计算资产组合的β系数和预期收益率；
(4)计算资产组合收益率与市场组合收益率的协方差(保留三位小数)；
(5)确定证券市场线的斜率和截距。
正确答案：
(1)某项资产的风险收益率=该项资产的口系数×市场风险溢酬
由此可知：
市场纽合的风险收益率=市场组合的β系数×市场风险溢酬
由于市场组合的β系数=1，因此，市场组合的风险收益率=1 ×市场风险溢酬=市场风险溢酬
即：市场风险溢酬=16%
甲股票的风险收益率=甲股票的β系数×16%
20%=甲股票的β系数×16%
解得：甲股票的β系数=1.25
由于甲股票的必要收益率=无风险收益率+甲股票的风险收益率
所以，25%=无风险收益率+20%
解得：无风险收益率=5%
(2)股票价格指数平均收益率=市场组合收益率=无风险收益率+市场风险溢酬=5%+16%=21%
(3)资产组合的β系数=0.6×1.25+0．4×0．8=1.07
由于资本资产定价模型成立(即假设市场是均衡的)，因此：
资产组合的预期收益率=资产组合的，必要收益率=无风险收益率+资产组合的口系数×市场风险溢酬=5%+1.07×16%=22.12%
(4)根据β系数的定义式可知：
乙股票的β系数=乙股票收益率与市场组合收益率的协方差/市场组合收益率的方差
资产组合的β系数=资产组合收益率与市场组合收益率的协方差/市场组合收益率的方差
即：0.8=40%/市场组合收益率的方差1.07=资产组合收益率与市场组合收益率的协方差/市场组合收益率的方差
解得：资产组合收益率与市场组合收益率的协方差=1.07 ×40%/0.8=0.535
(5)证券市场线的斜率=市场风险溢酬=16%
证券市场线的截距=无风险收益率=5%
-
第4题：
共用题干
假设资本资产定价模型成立，相关证券的风险与收益信息如表3-6所示。（注：表中的数字是相互关联的）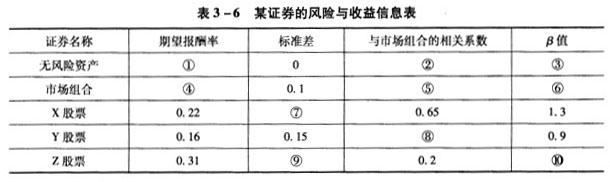
根据案例回答27～34题。根据表中其他信息可以得出⑧的值，即Y股票与市场组合的相关系数为()。
A:0.2
B:0.4
C:0.6
D:0.8答案：C解析：一个资产分散状况良好的投资组合必定已很好地分散和消除了非系统性风险，因此非系统性风险对该投资组合的收益水平不会造成很明显的影响。但是系统性风险是无法消除的，它对该投资组合的收益水平有较大影响。
对于无风险资产来说，其市场风险β值为0，即不存在；从而可知其与市场组合的相关系数为0。
对于市场组合来说，其市场风险β值为1；从而可知其与本身的相关系数为1。
利用X股票和Y股票的数据解联立方程：0.22=无风险资产报酬率+1.3*（市场组合报酬率-无风险资产报酬率）0.16=无风险资产报酬率+0.9*（市场组合报酬率-无风险资产报酬率）可得：无风险资产报酬率=0.025；市场组合报酬率=0.175。
β=与市场组合的相关系数*（股票标准差/市场组合标准差），即：1.3=0.65*（X股票标准差/0.1），进而可得：X股票标准差=0.2。
根据β值的计算公式求Y股票的相关系数：0.9=r*(0.15/0.1)，可得：r=0.6。
根据资本资产定价模型计算Z股票的β值：0.31=0.025+β*（0.175-0.025），可得：β=1.9。
根据β值的计算公式求z股票的标准差：1.9=0.2*（标准差/0.1），可得：标准差=0.95。 -
第5题：
某证券资产组合中有A、B、C三只股票，其中：A股票β系数为0.8，每股市价为4元，股票数量为800万股；B股票β系数为1.5，每股市价为8元，股票数量为100万股；C股票β系数为1.5，每股市价为25元，股票数量为160万股。该证券资产组合的β系数是（ ）。A.1
B.1.22
C.1.27
D.1.5答案：B解析：A股票比例＝（4×800）÷（4×800＋8×100＋25×160）＝40%；B股票比例＝（8×100）÷（4×800＋8×100＋25×160）＝10%；C股票比例＝（25×160）÷（4×800＋8×100＋25×160）＝50%。 -
第6题：
某证券资产组合中有A、B、C三只股票，所占的比重分别为60%、20%、20%。A股票的β系数为0.8，B股票的β系数为0.6，C股票的β系数为1。则证券资产组合的β系数是（ ）。A.0.6
B.0.8
C.1
D.2.4答案：B解析：证券资产组合的β系数=60%×0.8+20%×0.6+20%×1=0.8。 -
第7题：
现有A、B、C三种产品，其资产收益率的相关系数如表1—3所示，则（ ）。?
表1—3三种产品资产收益率的相关系数
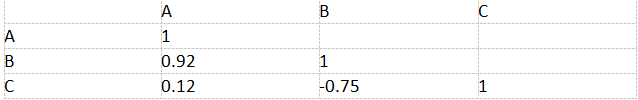A.B与C的组合可以很好的起到风险对冲的作用
B.A与B的组合可以很好地分散风险
C.A与C的组合不能起到风险分散的作用
D.B与C的组合不能很好地分散风险答案：A解析：风险对冲是指通过投资或购买与标的资产收益波动负相关的某种资产或衍生产品，来冲销标的资产潜在损失的一种策略性选择。如表1—3所示，产品A与产品B的资产收益率高度正相关，其组合不能很好地分散风险；产品A与产品C的资产收益率弱相关，产品B与产品C的资产收益率负相关，这两个组合都能起到风险分散的作用。
-
第8题：
假设A资产和B资产在不同经济状态下可能的收益率以及各种经济状态出现的概率如下表所示
A资产和B资产形成一个资产组合，A资产和B资产的投资比重各为50%。A、B资产收益率的相关系数为－1。 要求：
（1）计算资产组合的预期收益率；
（2）计算A资产和B资产收益率的标准差；
（3）计算资产组合的方差和标准差。答案：解析：1.A资产的预期收益率＝1/3×30%＋1/3×10%＋1/3×（－7%）＝11% B资产的预期收益率＝1/3×（－5%）＋1/3×7%＋1/3×19%＝7% 资产组合的预期收益率＝11%×50%＋7%×50%＝9%（1分）
2.A 资产收益率的标准差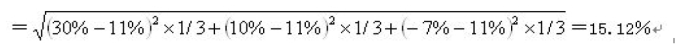
B资产收益率的标准差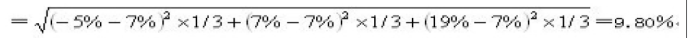
3.资产组合收益率的方差 ＝（0.5×15.12%） 2＋（0.5×9.80%） 2＋2×（－1）×（0.5×15.12%）×（0.5×9.80%） ＝（0.5×15.12%－0.5×9.80%） 2 ＝0.071%（1分） 资产组合收益率的标准差＝（0.071%） 1/2＝|0.5×15.12%－0.5×9.80%|＝2.66%（1分） -
第9题：
某证券资产组合的相关信息如下：A股票的贝塔系数为0.5，在组合中所占的比例为30%；B股票的贝塔系数为1.2，在组合中所占的比例为50%;C股票的贝塔系数为1.7，在组合中所占的比例为20%,则证券资产组合的贝塔系数为( )。A.1.02
B.1.09
C.1.13
D.1.20答案：B解析：证券资产组合的贝塔系数=0.5×30%+1.2×50%+1.7×20%=1.09。 -
第10题：
某资产组合包含两个资产，权重相同，资产组合的标准差为13。资产1和资产2的相关系数为0.5，资产2的标准差为19.50，则资产1的标准差为（）。
- A、1
- B、10
- C、20
- D、无法计算
正确答案:B -
第11题：
单选题下列有关β系数的表述不正确的是（ ）。A在运用资本资产定价模型时，某资产的β系数小于零，说明该资产风险小于市场平均风险
B在证券的市场组合中，所有证券的贝塔系数加权平均数等于1
C某股票的β值反映该股票收益率变动与整个股票市场收益率变动之间的相关程度
D投资组合的β系数是加权平均的β系数
正确答案： A解析：
A项，市场组合的β系数等于1，在运用资本资产定价模型时，某资产的β值小于1，说明该资产的系统风险小于市场风险。B项，市场组合的贝塔系数为1，而证券的市场组合可以理解为市场上所有证券所构成的投资组合，所以，在证券的市场组合中，所有证券的β系数加权平均数等于1；C项是β系数的含义；D项是组合贝塔系数的含义。 -
第12题：
问答题某公司拟进行股票投资，计划购买A、B、C三种股票，并分别设计了甲、乙两种资产组合。已知三种股票的β系数分别为1．5、1．0和0．5，它们在甲种资产组合下的投资比重为50％、30％和20％；乙种资产组合的风险收益率为3．4％。同期市场上所有股票的平均收益率为12％，无风险收益率为8％。 要求： (1)根据A、B、C股票的β系数，分别评价这三种股票相对于市场组合而言的投资风险大小。 (2)按照资本资产定价模型计算A股票的必要收益率。 (3)计算甲种资产组合的β系数和风险收益率。 (4)计算乙种资产组合的β系数和必要收益率。 (5)比较甲乙两种资产组合的β系数，评价它们的投资风险大小。正确答案： (1)由于市场组合的β系数为1，所以，根据A、B、C股票的β系数可知，A股票的投资风险大于市场组合的投资风险；B股票的投资风险等于市场组合的投资风险；C股票的投资风险小于市场组合的投资风险。
(2)A股票的必要收益率
＝8％＋1．5×(12％－8％)＝14％
(3)甲种资产组合的β系数
＝1．5×50％＋1．0×30％＋0．5×20％＝1．15
甲种资产组合的风险收益率
＝1．15×(12％－8％)＝4．6％
(4)乙种资产组合的β系数
＝3．4％／(12％－8％)＝0．85
乙种资产组合的必要收益率
＝8％＋3．4％＝11．4％
(5)甲种资产组合的β系数(1．15)大于乙种资产组合的β系数(0．85)，说明甲的投资风险大于乙的投资风险。解析： 暂无解析 -
第13题：
已知甲股票的风险收益率为12%，市场组合的风险收益率为10%，甲股票的必要收益率为16%，资本资产定价模型成立，乙股票的口系数为0.5，乙股票收益率与市场组合收益率的协方差为6%。
要求：
(1)计算甲股票的口系数、无风险收益率；
(2)计算股票价格指数平均收益率；
(3)确定证券市场线的斜率和截距；
(4)如果甲、乙构成的资产组合中甲的投资比例为0.6，乙的投资比例为0.4，计算资产组合的卢系数以及资产组合收益率与市场组合收益率的协方差；假设资产组合收益率的方差为16%，计算资产组合收益率与市场组合收益率的相关系数；
(5)如果甲的收益率标准差为15%，把甲、乙的投资比例调整为相等，即各为0.5，并假设甲股票收益率与乙股票收益率的相关系数为1，资产组合收益率的标准差为12%，计算乙股票收益率的标准差。
(4)假设市场是均衡的，计算所选项目的风险价值系数(b)；
(5)假设资本资产定价模型成立，计算市场风险溢酬、乙项目的口系数；
(6)计算乙项目收益率与市场组合收益率的相关系数。
正确答案：
(1)甲股票的风险收益率－甲股票的β系数×10%即：12%＝甲股票的口系数×10%
解得：甲股票的β系数＝1.2由于甲股票的必要收益率＝无风险收益率+甲股票的风险收益率
所以，16%＝无风险收益率+12%
解得：无风险收益率＝4%
(2)股票价格指数平均收益率－市场组合收益率
＝4%+10%＝14%
(3)证券市场线的斜率－市场风险溢酬＝10%证券市场线的截距－无风险收益率＝4%
(4)资产组合的β系数＝0.6×1.2+0.4×0.5＝0.92
根据口系数的定义公式可知：
乙股票的β系数－乙股票收益率与市场组合收益率的协方差/市场组合收益率的方差
即：0.5＝6%席场组合收益率的方差
解得：市场组合收益率的方差＝12%0.92＝资产组合收益率与市场组合收益率的协方差肺场组合收益率的方差
解得：资产组合收益率与市场组合收益率的协方莘＝0.92×12%＝11.04%
资产组合收益率与市场组合收益率的协方差－资产组合收益率与市场组合收益率的相关系数×资产组
合收益率的标准差×市场组合收益率的标准差即：11.04%－资产组合收益率与市场组合收益率的相关系数××解得：资产组合收益率与市场组合收益率的相关系数＝0.80
(5)在两项资产收益率的相关系数为1，投资比例相等的情况下，资产组合收益率的标准差＝两项资产收益率标准差的算数平均数，即：12%＝(15%4+乙股票收益率的标准差)/2，解得：乙股票收益率的标准差＝9%。 -
第14题：
关于相关系数的说法正确的是（ ）。
A．当相关系数＝1时，资产组合不能降低任何风险
B．当相关系数＝-1时，资产组合可以最大限度地抵消风险
C．当相关系数＝0时，表明两项资产的收益率之间不相关，资产组合不能抵消风险
D．当相关系数＝1时，资产组合的风险等于组合中各项资产风险的加权平均值
正确答案：AB
关于相关系数的说法正确的是（ ）。
A．当相关系数＝1时，资产组合不能降低任何风险
B．当相关系数＝-1时，资产组合可以最大限度地抵消风险
C．当相关系数＝0时，表明两项资产的收益率之间不相关，资产组合不能抵消风险
D．当相关系数＝1时，资产组合的风险等于组合中各项资产风险的加权平均值 -
第15题：
资产组合的贝塔系数与组合内的资产收益率的相关系数有关。()答案：错解析：资产组合的贝塔系数等于资产组合内各资产贝塔系数的加权平均，因此与组合内资产收益率的相关系数无关。 -
第16题：
某证券资产组合中有三只股票，A股票β系数为1.5，B股票β系数为1，C股票β系数为0.8，三只股票所占比重分别为0.2、0.4、0.4，则该证券资产组合的β系数为（）。A.0.98
B.1.02
C.1.10
D.1.12答案：B解析：该证券资产组合的β系数=1.5×0.2+1×0.4+0.8×0.4=1.02。 -
第17题：
下列关于β系数的表述中，错误的是（ ）。A.β系数可以为负数
B.某股票的β值反映该股票收益率变动与整个股票市场收益率变动之间的相关程度
C.投资组合的β系数一定会比组合中任一单项证券的β系数低
D.β系数反映的是单项资产或证券资产组合的系统风险答案：C解析：由于投资组合的β系数等于单项资产的β系数的加权平均数，所以，选项C的说法不正确。 -
第18题：
某资产组合包含两个资产，权重相同，资产组合的标准差为13。资产1和资产2的相关系数为0．5，资产2的标准差为19．50，则资产1的标准差为（ ）。A.1
B.10
C.20
D.无法计算答案：B解析：设资产1的标准差为σ，则根据公式：132=(0．5σ)2+(0．5×19．5)2+2×0．5×0．5×0．5×σ×19．5，解得σ=10。
-
第19题：
假设商业银行持有资产组合A，根据投资组合理论，下列哪种操作降低该组合风险的效果最差 （ ）A.卖出50％资产组合A，用于购买与资产组合A的相关系数为0的资产组合Y
B.卖出50％资产组合A，用于购买与资产组合A的相关系数为-0．5的资产组合Z
C.卖出50％资产组合A，持有现金
D.卖出50％资产组合A，用于购买与资产组合A的相关系数为+0．8的资产组合X答案：D解析：如果资产组合中各资产存在相关性，则风险分散的效果会随着各资产问的相关系数有所不同。假设其他条件不变，当各资产间的相关系数为正时，风险分散效果较差；当相关系数为负时，风险分散效果较好。 -
第20题：
甲公司现有一笔闲置资金，拟投资于某证券组合，该组合由X、Y、Z三种股票构成，资金权重分别为40%、30%和30%，β系数分别为2.5、1.5和1，其中X股票投资收益率的概率分布如下表所示。
Y、Z股票的预期收益率分别为10%和8%，当前无风险利率为4%，市场组合的必要收益率为9%。
要求：
（1）计算X股票的预期收益率。
（2）计算该证券组合的预期收益率。
（3）计算该证券组合β系数。
（4）利用资本资产定价模型计算该证券组合的必要收益率，并据以判断该证券组合是否值得投资。答案：解析：（1）X股票的预期收益率=30%×20%+50%×12%+20%×5%=13%
（2）该证券组合的预期收益率=40%×13%+30%×10%+30%×8%=10.6%
（3）该证券组合β系数=40%×2.5+30%×1.5+30%×1=1.75
（4）该证券组合的必要收益率=4%+1.75×（9%-4%）=12.75%
由于该证券组合的必要收益率12.75%大于该证券组合的预期收益率10.6%，所以该证券组合不值得投资。 -
第21题：
某客户的投资组合中仅两只股票，假设经过计算，两只股票的相关系数为0.8，则理财规划师可能会给出如下评价或建议（）。
- A、这两只股票相关程度较高
- B、风险分散化效应较高
- C、股票投资收益较低
- D、资产组合流动性好
- E、应适当调整投资组合
正确答案:A,E -
第22题：
问答题要求:(1)根据A、B、C股票的β系数，分别评价这三种股票相对于市场投资组合而言的投资风险大小。(2)按照资本资产定价模型计算A股票的必要收益率。(3)计算甲种投资组合的β系数和风险收益率。正确答案：解析： -
第23题：
多选题下列有关单项资产β系数的表述正确的有（ ）。A某单项资产的β系数可以反映该单项资产收益率与市场上全部资产的平均收益率之间的变动关系
B某单项资产的β系数可以反映该单项资产所含有的全部风险对市场组合平均风险的影响程度
C某单项资产的β系数等于该种资产与市场组合的相关系数乘以该资产的标准离差与市场标准离差的比值
D某单项资产的β系数等于该资产与市场资产组合的协方差除以市场资产组合的方差
正确答案： D,B解析：
B项，β系数只能衡量系统风险，而不是全部风险，所以应该是某单项资产的β系数可以反映该单项资产所含有的系统风险对市场组合平均风险的影响程度。