假设ABC公司股票目前的市场价格为50元，而在一年后的价格可能是60元和40元两种情况。再假定存在一份100股该种股票的看涨期权，期限是一年，执行价格为50元。投资者可以按l0%的无风险利率借款。购进上述股票且按无风险利率10%借人资金，同时售出一份100股该股票的看涨期权。则按照复制原理，下列说法正确的有（ ）。 A．购买股票的数量为50股 B．借款的金额是1818元 C．期权的价值为682元 D．期权的价值为844元

题目

假设ABC公司股票目前的市场价格为50元，而在一年后的价格可能是60元和40元两种情况。再假定存在一份100股该种股票的看涨期权，期限是一年，执行价格为50元。投资者可以按l0%的无风险利率借款。购进上述股票且按无风险利率10%借人资金，同时售出一份100股该股票的看涨期权。则按照复制原理，下列说法正确的有（ ）。 A．购买股票的数量为50股 B．借款的金额是1818元 C．期权的价值为682元 D．期权的价值为844元

相似考题

1.假设某公司股票目前的市场价格为25元，而在6个月后的价格可能是32元和18元两种情况。再假定存在一份l00股该种股票的看涨期权，期限是半年，执行价格为28元。投资者可以按10%的无风险年利率借款。购进上述股票且按无风险年利率10%借入资金，同时售出一份100股该股票的看涨期权。 要求： (1)根据单期二叉树期权定价模型，计算一份该股票的看涨期权的价值； (2)假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变，若把6个月的时间分为两期，每期3个月，若该股票收益率的标准差为0．35，计算每期股价上升百分比和股价下降百分比； (3)结合(2)，分别根据套期保值原理、风险中性原理和两期二叉树期权定价模型，计算一份该股票的看涨期权的价值。

2.假设ABC公司股票目前的市场价格为28元，而在6个月后的价格可能是40元和20元两种情况。再假定存在一份100股该种股票的看涨期权，期限是半年，执行价格为28元。投资者可以按10%的无风险年利率借款。购进上述股票且按无风险年利率10%借入资金，同时售出一份100股该股票的看涨期权。要求：(1)根据单期二叉树期权定价模型，计算一份该股票的看涨期权的价值。(2)假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变，若把6个月的时间分为两期，每期3个月，若该股票收益率的标准差为0.08，计算每期股价上升百分比和股价下降百分比。(3)结合(2)分别根据套期保值原理和风险中性原理，计算一份该股票的看涨期权的价值。

3.假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是35元和16元两种情况。再假定存在一份100股该种股票的看涨期权，期限是一年，执行价格为30元。投资者可以按10%的无风险利率借款。购进上述股票且按无风险利率10%借入资金，同时售出一份100股该股票的看涨期权。要求：(1)根据套期保值原理，计算套期保值比率、按无风险利率借入资金的数额以及一份该股票的看涨期权的价值。(2)根据风险中性原理，计算一份该股票的看涨期权的价值。(3)若目前一份100股该股票看涨期权的市场价格为306元，按上述组合投资者能否获利。

4.假设ABC公司股票目前的市场价格为45元，而在一年后的价格可能是58元和42元两种情况。再假设存在一份200股该种股票的看涨期权，期限是一年，执行价格为48元。投资者可以按10%的无风险利率借款。购进上述股票且按无风险利率10%借入资金，同时售出一份200股该股票的看涨期权，则套期保值比率为（ ）。A．125B．140C．220D．156

更多“假设ABC公司股票目前的市场价格为50元,而在一年后的价格可能是60元和40元两种情况。再假定存在一 ”相关问题

  • 第1题：

    假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是36元和16元两种情况。市场上有两种以该股票为标的资产的期权：看涨期权和看跌期权。每份看涨期权可以买入1股股票，每份看跌期权可卖出1股股票，两种期权执行价格均为30元，到期时间为一年，一年以内公司不会派发股利，无风险利率为每年10%。
    要求：
    （1）根据复制原理，计算一份该股票的看涨期权的价值，利用看涨期权-看跌期权平价定理，计算看跌期权的价值。
    （2）若目前一份该股票看涨期权的市场价格为3.6元，能否创建投资组合进行套利，如果能，应该如何创建该组合。


    答案：
    解析：
    （1）
    根据复制原理：



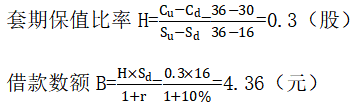
    一份该股票的看涨期权的价值=购买股票支出-借款=H×S0-B=0.3×24-4.36=2.84（元）
    看跌期权价值=30/（1+10%）+2.84-24=6.11（元）
    （2）
    由于目前一份该股票看涨期权的市场价格为3.6元，高于期权的价值2.84元，所以，可以创建组合进行套利，以无风险利率借入款项4.36元，购买0.3股股票，同时卖出一份该看涨期权，可以套利=3.6-（0.3×24-4.36）=0.76（元）。

  • 第2题：

    假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是30元和19.2元两种情况。现存在一份100股该种股票的看涨期权，期限是一年，执行价格为25元，一年以内公司不会派发股利，无风险年报价利率为10%。
    要求：
    （1）根据风险中性原理，计算一份该股票的看涨期权的价值。
    （2）根据复制原理，计算一份该股票的看涨期权的价值。
    （3）若目前一份100股该股票看涨期权的市场价格为306元，能否构建投资组合进行套利，如果能，应该如何构建该组合。


    答案：
    解析：
    （1）根据风险中性概率公式：
    期望报酬率=上行概率×股价上升百分比+下行概率×股价下降百分比
    =上行概率×股价上升百分比+（1-上行概率）×股价下降百分比
    股价上升百分比=（30-24）/24=25%，股价下降百分比=（19.2-24）/24=-20%
    假设上行概率为P，则：
    r=P×25%+（1-P）×（-20%）
    即：10%=P×25%+（1-P）×（-20%）
    求得：P=66.67%
    期权一年后的期望价值=66.67%×（30-25）×100+（1-66.67%）×0=333.35（元）
    期权价值=333.35/（1+10%）=303.05（元）。
    （2）根据复制原理：
    套期保值比率H=[（30-25）-0]/（30-19.2）×100=46.3（股）
    借款数额B=（46.3×19.2-0）/（1+10%）=808.15（元）
    一份该股票的看涨期权的价值=购买股票支出-借款=H×Sd-B=46.3×24-808.15=303.05（元）。
    （3）由于目前一份100股该股票看涨期权的市场价格为306元，高于期权的价值303.05元，所以，可以创建组合进行套利，以无风险利率借入款项808.15元，购买46.3股股票，同时卖出一份该看涨期权，可以套利306-（46.3×24-808.15）=2.95（元）。

  • 第3题：

    假设某公司股票目前的市场价格为49.5元，而一年后的价格可能是63.8元和46.2元两种情况。再假定存在一份200股该种股票的看涨期权，期限是一年，执行价格为52.8元。投资者可以购进上述股票且按无风险利率10%借入资金，同时售出一份200股该股票的看涨期权。则套期保值比率为（　　）。

    A、125
    B、140
    C、220
    D、156

    答案：A
    解析：
    套期保值比率=



    =125。

  • 第4题：

    假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是35元和16元两种情况。现存在一份100股该种股票的看涨期权，期限是一年，执行价格为30元，一年以内公司不会派发股利，无风险利率为每年10%。
    要求：
    （1）根据风险中性定理，计算一份该股票的看涨期权的价值。
    （2）根据复制原理，计算一份该股票的看涨期权的价值。
    （3）若目前一份100股该股票看涨期权的市场价格为306元，能否创建投资组合进行套利，如果能，应该如何创建该组合。


    答案：
    解析：
    （1）根据风险中性概率公式：
    期望报酬率=上行概率×股价上升百分比+下行概率×股价下降百分比
    =上行概率×股价上升百分比+（1-上行概率）×股价下降百分比
    股价上升百分比=（35-24）/24=45.83%，股价下降百分比=（16-24）/24=-33.33%
    假设上行概率为P，则：
    r=P×45.83%+（1-P）×（-33.33%）
    即：10%=P×45.83%+（1-P）×（-33.33%）
    求得：P=54.74%
    期权一年后的期望价值=54.74%×（35-30）×100+（1-54.74%）×0=273.7（元）
    期权的现值=273.7/（1+10%）=248.82（元）。
    （2）根据复制原理：



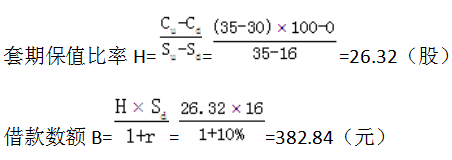
    一份该股票的看涨期权的价值=购买股票支出-借款=H×Sd-B=26.32×24-382.84=248.84（元）。
    （3）由于目前一份100股该股票看涨期权的市场价格为306元，高于期权的价值248.84元，所以，可以创建组合进行套利，以无风险利率借入款项382.84元，购买26.32股股票，同时卖出一份该看涨期权，可以套利306-（26.32×24-382.84）=57.16（元）。

  • 第5题：

    假设某公司股票目前的市场价格为49.5元，而一年后的价格可能是61.875元和39.6元两种情况。再假定存在一份200股该种股票的看涨期权，期限是一年，执行价格为52.8元。投资者可以购进上述股票且按无风险报价利率10%借入资金，同时售出一份200股该股票的看涨期权。则套期保值比率为（　　）。

    A.81.48
    B.91.48
    C.125
    D.156

    答案：A
    解析：
    套期保值比率=200×[（61.875-52.8）-0]/（61.875-39.6）=81.48。

相关内容