电灯泡耐用时间在1000小时以上的概率为0.2,求三只灯泡使用l000小时以后恰有一只坏与最多只有一只坏的概率.
题目
相似考题
更多“电灯泡耐用时间在1000小时以上的概率为0.2,求三只灯泡使用l000小时以后恰有一只坏与最多只有一只坏的概率.”相关问题
-
第1题:
误判率是指()A、好的判成坏的概率
B、坏的判成好的概率
C、漏检的概率
D、误收的概率
参考答案:D
-
第2题:
某种灯泡能用到3000小时以上的概率为0.8,能用到3500小时以上的概率为0.7,则一只已用到3000小时仍没有损坏的这种灯泡还可以用500小时以上的概率为?参考答案:P(A)=0.8,P(B)=0.7,P(AB)=P(B),∴P(B|A)=0.7/0.8=7/8
-
第3题:
电灯泡使用时数在1000小时以上的概率为0.2,求三个灯泡在1000小时以后最多有一个坏了的概率()
A、0.7
B、0.896
C、0.104
D、0.3
参考答案:C
-
第4题:
股票X和股票Y,这两只股票下跌的概率分别为0.4和0.5,两只股票至少有一只下跌的概率为0.7,那么,这两只股票同时下跌的概率为()。A:0.9
B:0.7
C:0.4
D:0.2答案:D解析: -
第5题:
张自强从多种开放式基金中任意选择一只进行定期定投,如果选中的那只开放式基金的净值小于0.8元的概率是0.2,净值在(0.8,0.9)元的概率是0.3,则净值不小于0.8元的概率是()。A:0.2
B:0.3
C:0.7
D:0.8答案:D解析:净值不小于0.8元的概率=1-0.2=0.8。 -
第6题:
设一设备在时间长度为t的时间内发生故障的次数N(t)~P(λt).
(1)求相继两次故障之间时间间隔T的概率分布;
(2)求设备在无故障工作8小时下,再无故障工作8小时的概率.答案:解析: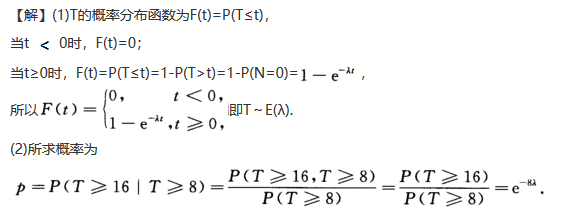
-
第7题:
使用正态分布表,可以进行的计算有( )A.根据Z分数求概率
B.根据概率求Z分数
C.根据概率求概率密度
D.根据Z值求概率密度答案:A,B,C,D解析:本题考查的是正态分布表的应用:(1)已知Z分数求概率,即已知标准分数求面积,有三种情况:①求某Z分数值与平均数之间的概率;②求某Z分数以上或以下的概率;③求两个Z分数之间的概率。(2)已知概率求z分数,即从面积求标准分数值,也有三种情况:①已知从平均数开始的概率值求Z值;②已知位于正态分布两端的概率值求该概率值分界点的Z值;③若已知正态曲线下中央部分的概率,求Z分数是多少。(3)已知概率或标准分数可查密度值、函数值。 -
第8题:
有35只小电灯泡串联,每只小电灯泡的电阻是23Ω,接入220V电源,求线路的电流强度。
正确答案: I=U/R=U/(35r)=220/(35×23)=0.27A
答:线路的电流强度是0.27A。 -
第9题:
使三只“110V40W”灯泡接入电源电压为220V的电路中都能正常工作,那么这些灯泡应该是()。
- A、全部串联
- B、每只灯泡串联适当电阻后再并联
- C、二只并联后与另一只串联
- D、二只串联后与另一只并联
正确答案:B -
第10题:
一只断了灯丝的电灯泡,灯丝接好后再使用,为什么比原来更亮?
正确答案: 灯丝断了,长度减小,电阻减小,根据P=U2/R可知,在电压一定时,电阻减小,电功率增大,所以会比原来更亮. -
第11题:
多选题合理抽样检验方案应具备的条件是()。A当交验批质量好时,应以高概率接收低概率拒收
B当交验批质量好时,应以低概率接收高概率拒收
C当交验批质量坏时,应以高概率接收低概率拒收
D当交验批质量坏时,应以低概率接收高概率拒收
正确答案: A,D解析: 暂无解析 -
第12题:
单选题船舶主配电板上装有三只绝缘指示灯,如其中有一只灯熄灭,其余两只灯比平时亮,说明()。A电网有一相接地
B电网有两相接地
C一只灯泡烧毁
D一相接地,一只灯泡烧毁
正确答案: B解析: 暂无解析 -
第13题:
飞机在雨天晚点的概率为0.8,在晴天晚点的概率为0.2,天气预报称明天有雨的概率为0.4,试求明天飞机晚点的概率.
正确答案:
-
第14题:
若将一只25瓦220V的电灯泡,接到1千瓦220V的发电机上,此灯泡会不会烧坏,为什么?参考答案:将一只25瓦220V的电灯泡,接到1千瓦220V的发电机上,灯泡不会烧坏;原因是虽然发电机输出功率大于灯泡的额定功率,发电机发出的电压与灯泡的额定电压相等,通过灯泡的电流仍为额定电流值,所以灯泡消耗的功率仍为25瓦,不会烧坏。
-
第15题:
对10000只灯泡进行耐用性能测试,根据以往资料,耐用时间标准差为51.91小时,若采用重复抽样方法,概率保证68.27%,平均耐用时数的误差范围不超过9小时。在这种条件下应抽取34只灯泡进行耐用性能测试。
A.正确
B.错误
正确答案:A
-
第16题:
张先生持有的一只股票,预计明日有0.2的概率上涨10%,有0.3的概率下跌5%,有0.5的概率上涨5%,则该股票明日的预期收益率为()。A:2.13%
B:3.00%
C:3.53%
D:5.00%答案:B解析:本题考查的是预期收益率的计算。该股票明日的预期收益率=0.2*10%+0.3*(-5%)+0.5*5%=3.00%。 -
第17题:
王先生持有三只股票,他预期明天至少有两只股票会上涨,则该事件的对立事件是()。A:最多有一只股票上涨
B:至少有一只股票上涨
C:三只股票都上涨
D:只有一只股票上涨答案:A解析:“至少有两只股票上涨”包括“两只股票上涨”和“三只股票都上涨”两种情况,那么与之相对应的情况是“只有一只股票上涨”或者“三只股票都没有上涨”,两种情况合起来称为“最多有一只股票上涨”。 -
第18题:
某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为( )A.0.008
B.0.104
C.0.096
D.1答案:B解析:【考情点拨】本题主要考查的知识点为分类计数原理. 【应试指导】已知灯泡使用1000小时后好的概率为0.2,坏的概率为1-0.2=0.8,则三个灯泡使用1000小时以.后,可分别求得: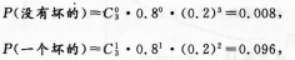
故最多只有一个坏的概率为:0.008+0.096=0.104. -
第19题:
有一只220V的电灯泡,灯泡的电阻是484Ω,当电源电压为220V时,求通过灯泡的电流?
通过灯泡的电流I=U/R=220/484=0.455(A)
略 -
第20题:
对某厂日产10000个灯泡的使用寿命进行抽样调查,抽取100个灯泡,测得其平均寿命为1800小时,标准差为6小时。要求: (1)按68.27%概率计算抽样平均数的极限误差; (2)按以上条件,若极限误差不超过0.4小时,应抽取多少只灯泡进行测试; (3)按以上条件,若概率提高到95.45%,应抽取多少灯泡进行测试? (4)若极限误差为0.6小时,概率为95.45%,应抽取多少灯泡进行测试? (5)通过以上计算,说明极限误差、抽样单位数和概率之间的关系。
正确答案: (1)极限误差为0.6小时
(2)应抽取225只灯泡进行测试
(3)应抽取900只灯泡进行测试
(4)应抽取400只灯泡进行测试
(5)极限误差大小、抽样单位数的多少和概率保证程度成正比关系。 -
第21题:
已知一只标有“220V、40W”的灯泡接在线路电压为220V的线路上,求该灯泡照明5小时后消耗多少电能(多少度点)?假设1度电单价为0.6元/度,求需要交电费多少?
正确答案: 根据公式W=Pt
代入已知
得W=0.04×5=0.2(度)
应交电费=0.2×0.6=0.12(元) -
第22题:
合理抽样检验方案应具备的条件是()。
- A、当交验批质量好时,应以高概率接收低概率拒收
- B、当交验批质量好时,应以低概率接收高概率拒收
- C、当交验批质量坏时,应以高概率接收低概率拒收
- D、当交验批质量坏时,应以低概率接收高概率拒收
正确答案:A,D -
第23题:
单选题10个灯泡中5个是好的,5个是坏的,混合在一起:(1)若随机有放回的抽取3个灯泡,这3个全是好的概率为多少?(2)如果一开始采用不放回的抽样,抽中3个全是好的概率为多少?正确答案: A解析:
