若y=e2x，则dy=_________．

题目

相似考题

1.（ 52 ）下列关于函数依赖和多值依赖的叙述中，哪些是不正确的？I ．若 X → Y, 则 X →→ Y Ⅱ ．若 X →→ Y, 则 X → YⅢ ．若 Y ? X, 则 X → Y Ⅳ ．若 Y ? X, 则 X →→ YⅤ ．若 X → Y, Y ’ ? X, 则 X → Y ’ Ⅵ ．若 X →→ Y, Y ’ ? Y, 则 X →→ Y ’A ） Ⅱ 和 ⅣB ） Ⅰ 、 Ⅲ 和 ⅣC ） Ⅱ 和 ⅥD ） Ⅳ 和 Ⅵ

2.下列关于函数依赖和多值依赖的叙述中，不正确的是( )。Ⅰ．若X→Y，则X→→YⅡ．若X→Y，则X→YⅢ．若YX，则X→YⅣ、若YX，则X→→YⅤ．若X→Y，Y*Y，则X→Y*Ⅵ．若X→→Y，Y*y，则X→→Y，A．Ⅱ和ⅣB．Ⅰ、Ⅲ和ⅣC．Ⅱ和ⅥD．Ⅳ和Ⅵ

3.下列关于函数依赖和多值依赖的叙述中，不正确的是( )。Ⅰ、若X→Y，则X→→YⅡ、若X→→Y，则X→YⅢ、若YX，则X→YⅣ、若YX，则X→→YⅤ、若X→Y，Y*Y，则X→Y*Ⅵ、若X→→Y，Y*Y，则X→→Y*A．仅Ⅱ和ⅣB．仅Ⅰ、 Ⅱ和ⅣC．仅Ⅱ和ⅥD．仅Ⅳ、Ⅴ和Ⅵ

4.（53）下列关于函数依赖和多值依赖的叙述中，（）是不正确的。Ⅰ、若X→Y，则X→→Y Ⅱ、若X→→Y，则X→YⅢ、若Y í X，则X→Y Ⅳ、若Y í X，则X→→YⅤ、若X→Y，Y* ì Y，则X→Y* Ⅵ、若X→→Y，Y*ìY，则X→→Y*A）仅Ⅱ和ⅣB）仅Ⅰ、Ⅱ和ⅣC）仅Ⅱ和ⅥD）仅Ⅳ、Ⅴ和Ⅵ

更多“若y=e2x，则dy=_________．”相关问题

第1题：

设y=ln（cosx），则微分dy等于：

答案：C
解析：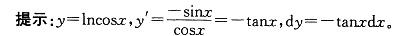
第2题：

设函数y=e2x，则y"(0)=_____．

答案：
解析：
填4．
第3题：

设y=1n(cosx)，则微分dy等于:

答案：C
解析：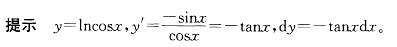
第4题：

若函数z=ln(xy)/y,则当x=e,y=e-1时，全微分dz等于（）。

A. edx + dy B. e2dx-dy C. dx + e2dy D. edx+e2dy

答案：C
解析：
正确答案是C。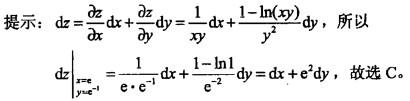
第5题：

设y=5+lnx，则dy=_______。

答案：
解析：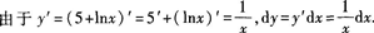
第6题：

设函数y＝e^2xcos3x，则dy＝（）。
- A、e^2x（2cos3x-3sin3x）
- B、e^2x（2cos3x-3sin3x）dx
- C、-6e^2xsin3xdx
- D、e^2x（2cos3x+3sin3x）dx
正确答案:B
第7题：

填空题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

正确答案： 1
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第8题：

单选题
若函数，则当x=e，y=e-1时，全微分dz等于（）。
A
edx+dy
B
e2dx-dy
C
dx+e2dy
D
edx+e2dy

正确答案： B
解析：暂无解析
第9题：

单选题
若u＝（x/y）1/z，则du（1，1，1）＝（　　）。
A
dx＋dy
B
dx－dy
C
－dx＋dy
D
－dx－dy

正确答案： C
解析：
因为du＝（∂u/∂x）dx＋（∂u/∂y）dy＋（∂u/∂z）dz，且∂u/∂x|_（1_，1_，1_）＝1，∂u/∂y|_（1_，1_，1_）＝－1，∂u/∂z|_（1_，1_，1_）＝0，故du＝dx－dy。
第10题：

填空题
设y＝f（lnx）ef（x），其中f可微，则dy＝____。

正确答案： [f′(lnx)e^f⁽^x⁾/x+f′(x)f(lnx)e^f⁽^x⁾]dx
解析：
由y′＝f′（lnx）e^f^（^x^）/x＋f′（x）f（lnx）e^f^（^x^），得dy＝[f′（lnx）e^f^（^x^）/x＋f′（x）f（lnx）e^f^（^x^）]dx。
第11题：

填空题
设函数y＝y（x）由方程y＝1－xey确定，则（dy/dx）|x＝0＝____。

正确答案： -e
解析：
设F（x，y）＝y－1＋xe^y，则dy/dx＝－F_x′/F_y′＝－e^y/（1＋xe^y）。x＝0时，y＝1，代入上式得（dy/dx）|_x_＝₀＝－e。
第12题：

单选题
下列关于函数依赖和多值依赖的叙述中，（）是不正确的。 Ⅰ、若X→Y，则X→→Y Ⅱ、若X→→Y，则X→Y Ⅲ、若YÍX，则X→Y Ⅳ、若YÍX，则X→→Y Ⅴ、若X→Y，Y*ÌY，则X→Y* Ⅵ、若X→→Y，Y*ÌY，则X→→Y*
A
仅Ⅱ和Ⅳ
B
仅Ⅰ、Ⅱ和Ⅳ
C
仅Ⅱ和Ⅵ
D
仅Ⅳ、Ⅴ和Ⅵ

正确答案： D
解析：暂无解析
第13题：

若f(u)可导，且y=f(ex)，则dy=（）

答案：B
解析：
【考情点拨】本题考查了复合函数的微分的知识点．
第14题：

若f(u)可导，且y=f(ex)，则dy=()

A.f'(ex)dx
B.f'(ex)exdx
C.f(ex)exdx
D.f'(ex)

答案：B
解析：
【考情点拨】本题考查了复合函数的微分的知识点．【应试指导】因为y=f(ex)，所以，y'=f'(ex)exdx．
第15题：

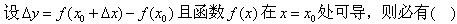
A.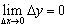
B.△y=0
C.dy=0
D.△y=dy

答案：A
解析：
第16题：

求函数f(x，y)=e2x(x+y2+2y)的极值.?

答案：
解析：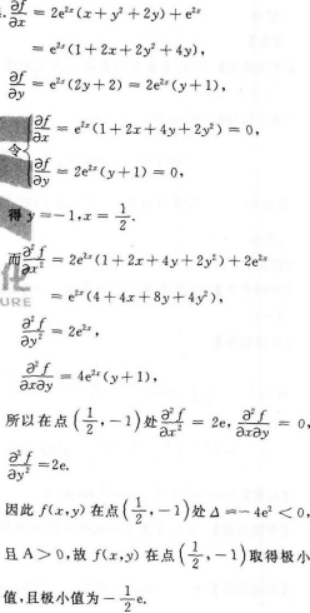
第17题：

设函数y=(x-3)4，则dy=__________．

答案：
解析：
4(x-3)3dx
第18题：

若函数，则当x=e，y=e-1时，全微分dz等于（）。
- A、edx+dy
- B、e2dx-dy
- C、dx+e2dy
- D、edx+e2dy
正确答案:C
第19题：

单选题
y″－4y＝e2x的通解为（　　）。
A
y＝C₁e^－^2x－（C₂＋x/4）e^－^2x（其中C₁，C₂为任意常数）
B
y＝C₁e^－^2x＋（C₂＋x/4）e^2x（其中C₁，C₂为任意常数）
C
y＝C₁e^－^2x＋（C₂＋x/4）e^－^2x（其中C₁，C₂为任意常数）
D
y＝C₁e^－^2x－（C₂＋x/4）e^2x（其中C₁，C₂为任意常数）

正确答案： D
解析：
原方程为y″－4y＝e^2x，其齐次方程对应的特征方程为r²－4＝0，解得r₁_，₂＝±2，故其对应的齐次方程y″－4y＝0的通解为y₁＝C₁e^－^2x＋C₂e^2x。因为非齐次方程右端的非齐次项为e^2x，2为特征方程的单根，故原方程特解可设为y^*＝Axe^2x，代入原方程得A＝1/4，故原方程的通解为y＝y₁＋y^*＝C₁e^－^2x＋C₂e^2x＋xe^2x/4，其中C₁，C₂为任意常数。
第20题：

单选题
若u＝（x/y）1/z，则du（1，1，1）＝（　　）。
A
dx/dy
B
dxdy
C
dx－dy
D
dx＋dy

正确答案： B
解析：
因为du＝（∂u/∂x）dx＋（∂u/∂y）dy＋（∂u/∂z）dz，且∂u/∂x|_（₁_，₁_，₁_）＝1，∂u/∂y|_（₁_，₁_，₁_）＝－1，∂u/∂z|_（₁_，₁_，₁_）＝0，故du＝dx－dy。
第21题：

填空题
y″－4y＝e2x的通解为____。

正确答案： y=C₁e^-^2x+(C₂+x/4)e^2x(其中C₁,C₂为任意常数)
解析：
原方程为y″－4y＝e^2x，其齐次方程对应的特征方程为r²－4＝0，解得r₁_，₂＝±2，故其对应的齐次方程y″－4y＝0的通解为y₁＝C₁e^－^2x＋C₂e^2x。因为非齐次方程右端的非齐次项为e^2x，2为特征方程的单根，故原方程特解可设为y^*＝Axe^2x，代入原方程得A＝1/4，故原方程的通解为y＝y₁＋y^*＝C₁e^－^2x＋C₂e^2x＋xe^2x/4。
第22题：

单选题
设y1＝e2x/2，y2＝exshx，y3＝exchx，则（　　）。
A
y₁，y₂，y₃都没有相同的原函数
B
y₂与y₃有相同的原函数，但与y₁的原函数不相同
C
y₁，y₂，y₃有相同的原函数e^x/（chx＋shx）
D
y₁，y₂，y₃有相同的原函数e^x/（chx－shx）

正确答案： B
解析：
由于y₁＝e^2x/2，y₂＝（e^2x/2）－1/2，y₃＝（e^2x/2）＋1/2，故三个函数的原函数都不相同。
第23题：

填空题
设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝____。

正确答案： (ln2-1)dx
解析：
2^xy＝x＋y等式两边求微分，得2^xyln2d（xy）＝dx＋dy，即2^xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|_x_＝₀＝（ln2－1）dx。

若y=e2x，则dy=_________．

题目

相似考题

更多“若y=e2x，则dy=_________．”相关问题

相关内容